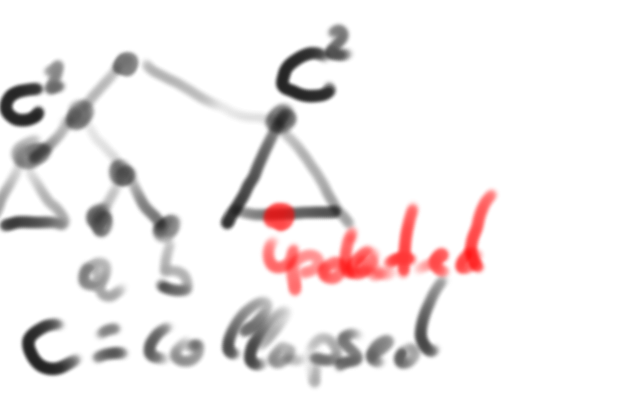
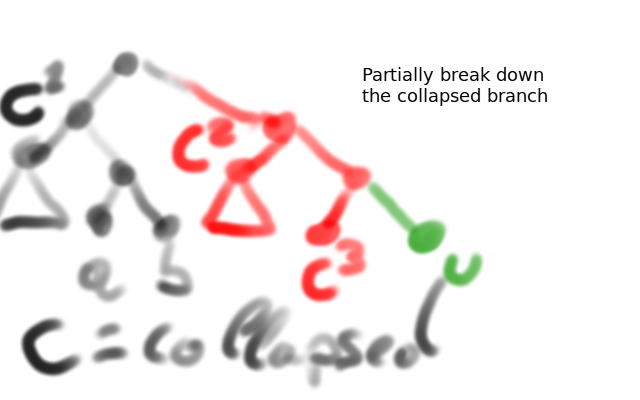
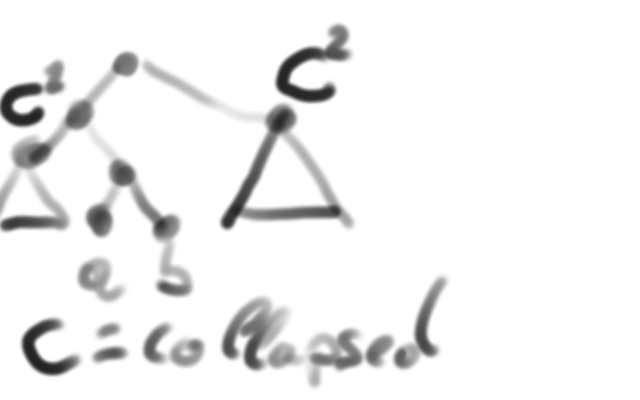Thesis

[Our focus is on compilers, not virtual machines or other run-time systems. We are also not concerned with parsers — there are lots of existing approaches and libraries which help writing parsers, although parsing in general is not yet a solved problem on all accounts.]Todo

[IR = the macroscopic structure of the program (i.e. the meta-model (explain what it is)) + the code of functions and/or methods (statements and expressions, basic blocks of statements, or bytecode instructions)]Todo

1.2 The challenges of writing compilers

Brain surgery? — It’s not exactly rocket science, is it?
That Mitchell & Webb Look, Series 3 — BBC Two

Compilers are an essential part of today’s software systems. Compilers translate high-level languages with complex semantics into lower-level languages. A compiler will parse the program, transform it in various ways, perform some more or less advanced static checks, and optimise the input program before producing an output in the desired target language. A compiler must be correct, reusable and fast. It must be correct because programmers are concerned with logical errors in their own code, and should not fear that the compiler introduces erroneous behaviour on its own. It must be also well-architectured: extensible, because the language is likely to evolve over time, modular in the hope that some components can be improved independently of the rest of the compiler (e.g. replacing or improving an optimisation phase, or changing the compiler’s front-end, to support another input language), and more generally reusable, so that parts can be repurposed to build other compilers, or other tools (analysers, IDEs, code instrumentation and so on). Finally, a fast compiler is desirable because the programmer’s edit-build-test cycle should be as frequent as possible[ (Sandberg 1988)]Todo.

Given their broad role, the complexity of the transformations involved, and the stringent requirements, writing compilers is a difficult task. Multiple pitfalls await the compiler engineer, which we will discuss in more detail below. This thesis aims to improve the compiler-writing toolkit currently available, in order to help compiler developers produce compilers which are closer to correctness, and easier to maintain.

The overall structure of a compiler will usually include a lexer and parser, which turn the program’s source into an in-memory representation. This initial representation will often be translated into an intermediate representation (IR) better suited to the subsequent steps. At some early point, the program will be analysed for syntactical or semantic inconsistencies (ranging from missing parentheses to duplicate definitions of the same variable), and may also perform a more thorough static analysis. Finally, code in the target language or for the target architecture is generated. The translation can additionally include optimisation phases in several spots: during code generation, using locally-recognisable patterns, or for example earlier, using the results of the program-wide analysis performed separately.

We identify three pitfalls which await the compiler-writer:

It is easy to reuse excessively a single intermediate representation type, instead of properly distinguishing the specifics of the input and output type of each pass;
There is a high risk associated with the definition of large, monolithic passes, which are hard to test, debug, and extend;
The fundamental structure of the program being compiled is often a graph, but compilers often work on an Abstract Syntax Tree, which requires explicit handling of the backward arcs; This is a source of bugs which could be avoided by using a better abstraction.

The first two issues are prone to manifestations of some form or another of the “god object” anti-pattern11 The “god object” anti-pattern describes object-oriented classes which do too much or know too much. The size of these classes tends to grow out of control, and there is usually a tight coupling between the methods of the object, which in turn means that performing small changes may require understanding the interactions between random parts of a very large file, in order to avoid breaking existing functionality.. The last issue is merely caused by the choice of an abstraction which does not accurately represent the domain. We will discuss each of these ailments in more detail in the following sections, and detail the undesirable symptoms associated with them.

1.2.1 Large monolithic passes

Large, monolithic passes, which perform many transformations simultaneously have the advantage of possibly being faster than several smaller passes chained one after another. Furthermore, as one begins writing a compiler, it is tempting to incrementally extend an initial pass to perform more work, rather than starting all over again with a new intermediate representation, and a new scaffolding to support its traversal.

However, the drawback is that large compiler passes are harder to test (as there are many more combinations of paths through the compiler’s code to test), harder to debug (as many unrelated concerns interact to some extent with each other), and harder to extend (for example, adding a new special form to the language will necessitate changes to several transformations, but if these are mingled in a single pass, the changes may be scattered through it, and interact with a significant amount of surrounding code). This higher maintenance cost also comes with another drawback: formal verification of the compiler will clearly be more difficult when large, tangled chunks of code which handle different semantic aspects are involved.

[Talk a bit about compcert here (one of the few/ the only formally verified compilers).]Todo

1.2.2 Overusing a single intermediate representation

The static analysis, optimisation and code generation phases could in principle work on the same intermediate representation. However, several issues arise from this situation.

In principle, new information gained by the static analysis may be added to the existing representation via mutation, or the optimiser could directly alter the IR. This means that the IR will initially contain holes (e.g. represented by null values), which will get filled in gradually. Manipulating these parts is then risky, as it is easy to accidentally attempt to retrieve a value before it was actually computed. Using the same IR throughout the compiler also makes it difficult for later passes to assume that some constructions have been eliminated by previous simplification passes, and correctness relies on a fixed order of execution of the passes; parts of the code which access data introduced or modified by other passes are more brittle and may be disrupted when code is refactored (for example, when moving the computation of some information to a later pass).

This situation becomes worse during the maintenance phase of the compiler’s lifecycle: when considering the data manipulated by a small portion of code (in order to fix or improve said code), it is unclear which parts are supposed to be filled in at that point, as well as which parts have been eliminated by prior simplification passes.

Furthermore, a mutable IR hinders parallel execution of compiler passes. Indeed, some compiler passes will perform global transformations or analyses, and such code may be intrinsically difficult to parallelise. Many other passes however are mere local transformations, and can readily be executed on distinct parts of the abstract syntax tree, as long as there is no need to synchronise concurrent accesses or modifications.

Using immutable intermediate representations (and performing shallow copies when updating data) can help with this second issue. However, there is more to gain if, instead of having many instances of the same type, each intermediate representation is given a distinct, precise type. The presence or absence of computed information can be known from the input and output type of a pass, instead of relying on the order of execution of the passes in order to know what the input data structure may contain.

1.2.3 Graphs

Nontrivial programs are inherently graphs: they may contain mutually recursive functions (which directly refer to each other, and therefore will form a cycle in a representation of the program), circular and (possibly mutually) recursive datatypes may syntactically contain (possibly indirect) references to themselves, and the control flow graph of a function or method can, as its name implies, contain instructions which perform conditional or unconditional backwards branches.

However, nearly every compiler textbook will mention the use of Abstract Syntax Trees (ASTs) to represent the program. This means that a structure, which intrinsically has the shape of a graph, is encoded as a tree.

Edges in the graph which may embody backward references can be made explicit in various ways:

By using a form of unique identifier like a name bearing some semantic value (e.g. the fully qualified name of the type or function that is referred to), an index into an array of nodes (e.g. the offset of an instruction in a function’s bytecode may be used to refer to it in the control flow graph), an automatically-generated unique identifier.
Manipulation of these identifiers introduces a potential for some sorts of bugs: name clashes can occur if the chosen qualification is not sufficient to always distinguish nodes. Thus compiler passes which duplicate nodes (for example specialising functions) or merge them must be careful to correctly update identifiers.
Anecdotally, we can mention a bug in the "Mono.Cecil" library (which allows easy manipulation of .NET bytecode). When “resolving” a reference to a primitive type, it can happen in some cases that "Mono.Cecil" returns a Type metadata object which references a type with the correct name, but [exported]Todo from the wrong DLL library.
Alternatively, backward references may be encoded as a form of path from the referring node. De Bruijn indices can be used in such an encoding, for example.
Once again, manipulating these references is risky, and De Bruijn indices are particularly brittle, for example when adding a wrapper around a node (i.e. adding an intermediate node on the path from the root), the De Bruijn indices used in some of the descendents of that node (but not all) must be updated. It is understandably easy to incorrectly implement updates of these indices, and a single off-by-one error can throw the graph’s representation into an inconsistent state.
The program’s representation could also contain actual pointers (thereby really representing the program as an “Abstract Syntax Graph”), using mutation to patch nodes after they are initially created.
In order to prevent undesired mutation of the graph after it is created, it is possible to “freeze” the objects contained within[references]Todo. This intuitively gives guarantees similar to those obtained from a purely immutable representation. However, the use of mutation could obstruct formal verification efforts, as some invariants will need to take into account the two phases of an object’s lifetime (during the creation of the containing graph, and after freezing it). More generally speaking, it is necessary to ensure that no mutation of objects happens during the graph construction, with the exception of the mutations required to patch cycles.
The compiler could also manipulate lazy data structures, where the actual value of a node in the graph is computed on the fly when that node is accessed.
Lazy programs are however harder to debug (Morris 1982; Nilsson and Fritzson 1993; Wadler 1998), as the computation of the various parts of the data manipulated does not occur in an intuitive order. Among other things, accidental infinite recursion could be triggered by totally unrelated code which merely reads a value.
Finally, Higher-Order Abstract Syntax, or HOAS for short, is a technique which encodes variable bindings as anonymous functions in the host language (whose parameters reify bindings at the level of the host language). Variable references are then nothing more than actual uses of the variable at the host language’s level. Substitution, a common operation in compilers and interpreters, then becomes a simple matter of calling the anonymous function with the desired substitute. HOAS has the additional advantage that it enforces well-scopedness, as it is impossible to refer to a variable outside of its scope in the host language.
Parametric HOAS, dubbed PHOAS, also allows encoding the type of the variables in the representation. [Can extra information other than the type be stored?]Todo
There are a few drawbacks with HOAS and PHOAS:
The “target” of a backward reference must be above all uses in the tree (i.e. a node may be the target of either backward references, forward references, but not a mix of both). This might not always be the case. For example, pre/post-conditions could, in an early pass in the compiler, be located outside of the normal scope of a function’s signature, but still refer to the function’s parameters. If the pre/post-condition language allows breaking encapsulation, these could even refer to some temporary variables declared inside the function.
[PHOAS naturally lends itself to the implementation of substitutions, and therefore is well-suited to the writing of interpreters. However, the representation cannot be readily traversed and accessed as would be done with normal structures, and therefore the model could be counterintuitive.]Todo
[It seems difficult to encode an arbitrary number of variables bound in a single construct (e.g. to represent bound type names across the whole program, or an arbitrary number of mutually-recursive functions declared via let … and … in …, with any number of and clauses in the compiled language.]Todo

Although some of these seem like viable solutions (e.g. explicitly freezing objects), they still involve low-level mechanisms to create the graph. When functionally replacing a node with a new version of itself, all references to it must be updated to point to the new version. Furthermore, code traversing the graph to gather information or perform updates needs to deal with cycles, in order to avoid running into an infinite loop (or infinite recursion). Finally, backward edges are not represented in the same way as forward edges, introducing an arbitrary distinction when fetching data from the neighbours of a node. This last aspect reduces the extensibility of code which manipulates graphs where access to fields is not done uniformly: supposing new features of the language to be compiled require turning a “seamless” edge into one which must be explicitly resolved in some way (e.g. because this node, in the updated IR, may now be part of cycles), this change of interface will likely break old code which relied on seamless access to that field.

We think that the compiler engineer could benefit from abstracting over these implementation details, and think of compiler passes in terms of graph transformations. Programmers using functional languages often write list transformations using functions like map, foldl, filter, zip and so on, instead of explicitly writing recursive functions.

The graph can be manipulated by updating some or all nodes of a given type, using an old-node to new-node transformation function. This transformation function could produce more than one node, by referencing the extra nodes from the replacement one. It should furthermore be possible to locally navigate through the graph, from its root and from the node currently being transformed. This interface would allow to seamlessly handle cycles — transformations which apply over a whole collection of nodes need not be concerned with cycles — and still allow local navigation, without distinguishing backward and forward edges.

1.2.4 Expressing the data dependencies of a pass via row types

It is easy enough to test a compiler by feeding it sample programs and checking that the compiled output behaves as expected. However, a specific set of conditions inside a given pass, in order to achieve reasonably complete code coverage, may prove to be a harder task: previous passes may modify the input program in unexpected ways, and obtaining a certain data configuration at some point in the compiler requires the developer to mentally execute the compiler’s code backwards from that point, in order to determine the initial conditions which will produce the desired configuration many steps later. This means that extensively testing corner cases which may occur in principle, but are the result of unlikely combinations of features in the input program, is a cumbersome task.

If the compiler consists of many small passes, whose inputs and outputs are serializable, then it becomes possible to thoroughly test a single pass in isolation, by supplying an artificial, crafted input, and checking some properties of its output.

However, a compiler written following the Nanopass philosophy will feature many small passes which read and update only a small part of their input. Specifying actual values for the irrelevant parts of the data not only makes the test cases more verbose than they need to be, but also hides out of plain sight which variations of the input matter (and may thus allow the detection of new errors), and which parts of the input are mere placeholders whose actual value will not influence the outcome of the pass, aside from being copied over without changes.

It is desirable to express, in a statically verifiable way, which parts of the input are relevant, and which parts are copied verbatim (modulo updated sub-elements). Furthermore, it would be useful to be able to only specify the relevant parts of tests, and omit the rest (instead of supplying dummy values).

Row polymorphism allows us to satisfy both expectations. The irrelevant fields of a record and the irrelevant cases of a variant type can be abstracted away under a single row type variable. “Row” operations on records allow reading and updating relevant fields, while keeping the part abstracted by the row type variable intact. When invoking a compiler pass, the row type variables may be instantiated to the full set of extra fields present in the real IR, when the pass is called as part of the actual compilation; it is also possible, when the pass is called during testing, to instantiate them to an empty set of fields (or to use a single field containing a unique identifier, used to track “object identity”).

1.2.5 Verification

[Needs a transition from the previous section, or this should be moved elsewhere.]Todo

The implementation presented in this thesis cannot be immediately extended to support end-to-end formal verification of the compiler being written. However, it contributes to pave the way for writing formally verified compilers: firstly, the smaller passes are easier to verify. Secondly, the use of intermediate representations which closely match the input and output data can be used, given a formal semantic of each IR, to assert that a transformation pass is systematically preserving the semantics of the input. Thirdly, the use of a typed language instead of the currently “untyped” Nanopass framework means that a lot of properties can be ensured by relying on the type system. Typed Racket’s type checker is not formally verified itself and would have to be trusted (alternatively, the adventurous researcher could attempt to derive well-typedness proofs automatically by hijacking the type checker to generate traces of the steps involved, or manually, only using the type checker as a helper tool to detect and weed out issues during development. Fourthly, the explicit specification of the dependencies of passes on their input via row types is a form of frame specification, and can significantly ease the verification effort, as the engineer can rely on the fact that irrelevant parts were not modified in the output. These are statically enforced by our extension of Typed Racket’s type system, which we formalise in chapter [??]Todo. This relies on trusting Typed Racket itself once again, and on the correctness of the implementation of our translation from the extended type system to Typed Racket’s core type system. Fifthly, we provide means to express graph transformations as such instead of working with an encoding of graphs as abstract syntax trees (or directed acyclic graphs), with explicit backward references. We are hopeful that eliminating this mismatch will be beneficial to the formal verification of the transformation passes.

These advantages would be directly available to engineers attempting a formal proof of their compiler, while trusting the correctness of Typed Racket, as well as that of our framework. The implementation of our framework is not hardened, and Typed Racket itself suffers from a small number of known sources of unsoundness22 See https://github.com/racket/typed-racket/issues., however. In order to do an end-to-end verification of a compiler, it would be necessary to port our approach to a language better suited to formal verification. Alternatively, Racket could in principle be extended to help formalisation efforts. Two approaches come to mind: the first consists in proving that the macros correctly implement the abstraction which they attempt to model; the second would be to have the macros inject annotations and hints indicating properties that must be proven, in the same way that type annotations are currently inserted. These hints could then be used by the prover to generate proof obligations, which could then be solved manually or automatically.

Mixing macros and language features which help obtaining static guarantees is a trending topic in the Racket ecosystem and in other communities.

Typed Racket is still in active development, and several other projects were presented recently.

Hackett33 https://github.com/lexi-lambda/hackett, mainly developed by King, is a recent effort to bring a Haskell 98-like type system to Racket.

Hackett is built on the techniques developed by Chang, Knauth and Greenman in (Chang et al. 2017), which lead to the Turnstile library44 https://bitbucket.org/stchang/macrotypes.git. Turnstile is a helper library which facilitates the creation of typed languages in Racket. Macros are amended with typing rules, which are used to thread type information through uses of macros, definition forms and other special forms. Type checking is therefore performed during macro-expansion, and does not rely on an external type checker which would work on the expanded code. As a result, new languages built with Racket and Turnstile are not limited to a pre-existing type system, but can rather devise their own from the ground up. This approach brings a lot of flexibility, the drawback being that more trust is put in the language designer.

The work presented in this thesis aims to follow a different path than that followed by Turnstile: we chose to implement our extended type system as an abstraction over the existing type system of Typed Racket. This means that we do not rely so much on the correctness of our typing rules: instead of verifying ourselves the well-typedness of compilers written using our framework, we inject type annotations in the expanded code, which are then verified by Typed Racket. Therefore, we are confident that type errors will be caught by Typed Racket, safe in the knowledge that the code obtained after macro-expansion is type-safe55 We actually use on a few occasions unsafe-cast. Such a blunt instrument is however only used in cases where Typed Racket already has the required type information, but the type checker fails to deduce the equivalence between two formulations of the same type, or does not acknowledge that the term being checked has the expected type. These issues are being worked on by the developers of Typed Racket, however, and we hope to be able to remove these uses of unsafe-cast in later versions.. This increased serenity comes at the cost of flexibility, as Typed Racket’s type system was not able to express the type constructs that we wanted to add. We therefore had to resort to a few hacks to translate our types into constructs that could be expressed using Typed Racket.

The approach of building more complex type constructs atop a small trusted kernel has been pursued by Cur66 https://github.com/wilbowma/cur, developed by Bowman. Cur is a dependently typed language which permits theorem proving and verified programming. It is based on a small kernel (the Curnel), which does not contain language features which can be expressed by macro transformations. Most notably, the prover’s tactics are defined using metaprogramming tools, and are not part of the core language.

Another tool worth mentioning is Rosette77 https://github.com/emina/rosette[reference]Todo. Rosette, mainly developed by Torlak, is a solver-aided language: it tightly integrates an SMT solver with some Racket constructs, so that powerful queries can be performed and answered, for example “what input values to the function f will generate outputs which satisfy the predicate p?”. It can also generate simple functions which satisfy given conditions. These features allow it to be used both as a helper tool during development, for engineers coming from various domains, and as a verifier, as the solver can be used to assert that a function will never give an erroneous output, given a set of constraints on its input.

The idea of expressing the type of macro transformations at some level (e.g. by indicating the type of the resulting expression in terms of the type of the input terms, as is allowed by Turnstile) is not new: in 2001, Ganz, Sabry and Taha already presented in 2001 MacroML (Ganz et al. 2001), an experimental language which allows type checking programs before macro-expansion. However, it seems that there is interest, both in the Racket community and elsewhere, for languages with powerful metaprogramming facilities, coupled with an expressive type system. We are hopeful that this will lead to innovations concerning the formal verification of programs making heavy use of complex macros.

1.3 Summary

Once upon a time…
Unknown

1.3.1 Extensible type system

We implemented a different type system on top of Typed Racket, using macros. Macros have been used not only to extend a language’s syntax (control structures, contract annotations, and so on), but also to reduce the amount of “boilerplate” code and obtain clearer syntax for common or occasional tasks. Macros have further been used to extend the language with new paradigms, like adding an object system (CLOS (Bobrow et al. 1988)[is it really implemented using macros?]Todo, Racket classes (Flatt et al. 2006)) or supporting logic programming (Racket Datalog and Racklog, Rosette (Torlak and Bodik 2013, 2014)). In the past, Typed Racket (Tobin-Hochstadt and Felleisen 2008) has proved that a type system can be successfully fitted onto an existing “untyped” language, using macros. We implemented the type-expander library atop Typed Racket, without altering Typed Racket itself. Our type-expander library allows macros to be used in contexts where a type is expected.

This shows that an existing type system can be made extensible using macros, without altering the core implementation of the type system. We further use these type expanders to build new kinds of types which were not initially supported by Typed Racket: non-nominal algebraic types, with row polymorphism. Typed Racket has successfully been extended in the past (for example by adding type primitives for Racket’s class system, which incidentally also support row polymorphism), but these extensions required modifications to the trusted core of Typed Racket. Aside from a small hack (needed to obtain non-nominal algebraic types which remain equivalent across multiple files), our extension integrates seamlessly with other built-in types, and code using these types can use idiomatic Typed Racket features.

Typed Racket was not initially designed with this extension in mind, nor, that we know of, was it designed with the goal of being extensible. We therefore argue that a better choice of primitive types supported by the core implementation could enable many extensions without the need to resort to hacks the like of which was needed in our case. In other words, a better design of the core types with extensibility in mind would have made our job easier.

In particular, Types in Typed Clojure (Bonnaire-Sergeant et al. 2016) support fine-grained typing of heterogeneous hash tables, this would likely allow us to build much more easily the “strong duck typing” primitives on which our algebraic data types are based, and without the need to resort to hacks.

In languages making heavy uses of macros, it would be beneficial to design type systems with a well-chosen set of primitive types, on top of which more complex types can be built using macros.

Building the type system via macros atop a small kernel is an approach that has been pursued by Cur, a dependently-typed language developed with Racket, in which the tactics language is entirely built using macros, and does not depend on Cur’s trusted type-checking core.

1.3.2 Compiler-writing framework

Our goal was to introduce a compiler-writing framework, which:

Supports writing a compiler using many small passes (in the spirit of Nanopass)
Allows writing the compiler in a strongly-typed language
Uses immutable data structures for the Intermediate Representations (ASTs)
Supports backwards branches in the AST, making it rather an Abstract Syntax Graph (this is challenging due to the use of immutable data structures).
Provides easy manipulation of the Intermediate Representations: local navigation from node to node, global higher-order operations over many nodes, easy construction, easy serialization, with the guarantee that at no point an incomplete representation can be manipulated. These operations should handle seamlessly backwards arcs.
Enforces structural invariants (either at compile-time or at run-time), and ensures via the type system that unchecked values cannot be used where a value respecting the invariant is expected.
Has extensive support for testing the compiler, by allowing the generation of random ASTs [(note that the user guides the random generation, it’s not fully automatic like quickcheck)]Todo, making it possible to read and write ASTs from files and compare them, and allows compiler passes to consume ASTs containing only the relevant fields (using row polymorphism).

1.3.3 Overview

The rest of this document is structured as follows:

Chapter 2 presents related work. It discusses approaches to extensible type systems in Section 2.1. Section 2.2 considers how structures, variants and polymorphism may exhibit different properties in different languages, and makes the case for bounded row polymorphism as a well-suited tool for building compilers. The Nanopass Compiler Framework is presented in Section 2.3, and techniques used to encode and manipulate graphs are studied in Section 2.4.
In Chapter 3, we give some example uses of the compiler framework described in this thesis. We indicate the pitfalls, bugs and boilerplate avoided thanks to its use. [Move this above the related work?]Todo
Chapter 4 gives an overview of the features of Typed Racket’s type system. It then formalises the features relevant to our work, by giving the subtyping rules, as well as the builder and accessor primitives for values of these types.
Section 5.1 explains how we implemented support for type-level macros as an extension to Typed Racket, without modifying the core implementation. We detail the reduction rules which allow translating a type making use of expanders into a plain type.
Section 5.2 discusses the flavour of algebraic datatypes which we chose to implement atop Typed Racket, as well as its extension with row types. We explain in detail our goals and constraints, and present two implementations — a first attempt, which unfortunately required verbose annotations for some “row operations”, and a second solution, which greatly reduces the number of annotations required, by using a different implementation strategy. We give formal semantics for these extensions, give the reduction rules which translate them back to Typed Racket’s type system, and show that this reduction preserves the original semantics. We then finally define a layer of syntactic sugar which allows convenient use of these new type primitives.
Section 6.1 builds upon these algebraic datatypes and row types to define a typed version of the Nanopass Compiler Framework which operates on abstract syntax trees. We explain the notions of tree nodes, mapping functions and cata-morphisms, show how these interact with row typing, and give an overview of the implementation. We then extend this with detached mappings: this feature allows the user to map a function over all nodes of a given type in a graph, regardless of the structure of the graph outisde of the relevant parts which are manipulated by the mapping function. This allows test data to not only omit irrelevant branches in the abstract syntax tree by omitting the field pointing to these branches, but also irrelevant parts located above the interesting nodes. In other words, this feature allows cutting and removing the top of the abstract syntax tree, and glue together the resulting forest. We also formally describe the result of applying a set of detached or regular mapping functions to an input tree.
Section 6.2 extends this typed version of Nanopass to handle directed acyclic graphs. We start by considering concerns such as equality of nodes (for which the previous chapter assumed a predicate existed, without actually implementing it), and hash consing. This allows us to prepare the ground for the extension presented in the next chapter, namely graphs.
We can then introduce support for cycles in Section 6.3: instead of describing abstract syntax tree transformations, it then becomes possible to describe graphs transformations. To this end, we introduce new kinds of nodes: placeholders, which are used during the construction of the graph, with-indices nodes, which encode references to neighbouring nodes as indices into arrays containing all nodes of a given type, for the current graph, and with-promises nodes, which hide away this implementation detail by lazily resolving all references, using a uniform API. This allows all fields of a given node to be accessed in the same way, while still allowing logical cycles built atop a purely immutable representation.
We give an overview of how our implementation handles cycles, using worklists which gather and return placeholders when the mapping functions perform recursive calls, and subsequently turn the results into into with-indices nodes, then into with-promises ones. We then update our notion of equality and hash consing to account for cycles, and update the formal semantics too.
Extra safety can be obtained by introducing some structural invariants which constrain the shape of the graph. For example, it is possible to ensure the well-scopedness of variable references. Another desirable property would be the absence of cycles, either to better model the IR, knowing that cyclic references are not allowed at some point by the target language, or to detect early on changes in the IR which may break code assuming the absence of cycles. A third option would be to ensure that “parent” pointers are correct, and that the node containing them is indeed referenced by the parent (i.e., ensure the presence of well-formed cycles). Section 6.4 presents an extension of our graph manipulation framework, which allows the specification of structural invariants. These can in some cases be checked statically, in other cases it may be necessary to follow a macro-enforced discipline, and as a last resort, a dynamic check may be performed.
We further explain how we use phantom types to reflect at the type level which invariants were checked on an instance of a graph. The types used to represent that an instance satisfies an invariant are chosen so that instances with stronger invariants are subtypes of instances with weaker invariants.
Finally, in Section 6.5 we succinctly present some extensions which could be added to the framework presented in the previous chapters. We discuss how it would be possible to garbage-collect unused parts of the graph when only a reference to an internal node is kept, and the root is logically unreachable. Another useful feature would be the ability to define general-purpose graph algorithms (depth-first traversal, topological sort, graph colouring, and so on), operating on a subset of the graph’s fields. This would allow to perform these common operations while considering only a subgraph of the one being manipulated. Finally, we mention the possibility to implement an α-equivalence comparison operator.
In Chapter 7, we present more examples and revisit the initial examples illustrating our goals in the light of the previous chapters.
We ported the most complete compiler written with Nanopass (a Scheme compiler) to our framework; we summarise our experience and compare our approach with Nanopass, by indicating the changes required, in particular how many additional type annotations were necessary.
Finally, we conclude and list future work directions.

2 State of the art

\def\ifmathjax#1{#1}\def\iflatex#1{}

2.1 Extending the type system via macros

Our work explores one interesting use of macros: their use to extend a programming language’s type system.

Chang, Knauth and Greenman (Chang et al. 2017) took the decision to depart from Typed Racket, and implemented a new approach, which allows type systems to be implemented as macros. Typing information about identifiers is threaded across the program at compile-time, and macros can decide whether a term is well-typed or not.

Another related project is Cur88 https://github.com/wilbowma/cur, a dependent type system implemented using Racket macros.

Bracha suggests that pluggable type systems should be used (Bracha 2004). Such a system, JavaCOP is presented by Andreae, Noble, Markstrum and Shane (Andreae et al. 2006) as a tool which “enforces user-defined typing constraints written in a declarative and expressive rule language”.

In contrast, Typed Racket (Tobin-Hochstadt and Felleisen 2008) was implemented using macros on top of “untyped” Racket, but was not designed as an extensible system: new rules in the type system must be added to the core implementation, a system which is complex to approach.

Following work by Asumu Takikawa99 https://github.com/racket/racket/pull/604, we extended Typed Racket with support for macros in the type declarations and annotations. We call this sort of macro “type expanders”, following the commonly-used naming convention (e.g. “match expanders” are macros which operate within patterns in pattern-matching forms). These type expanders allow users to easily extend the type system with new kinds of types, as long as these can be translated back to the types offered natively by Typed Racket.

While the Type Systems as Macros by Chang, Knauth and Greenman (Chang et al. 2017) allows greater flexibility by not relying on a fixed set of core types, it also places on the programmer the burden of ensuring that the type checking macros are sound. In contrast, our type expanders rely on Typed Racket’s type checker, which will still catch type errors in the fully-expanded types. In other words, writing type expanders is safe, because they do not require any specific trust, and translate down to plain Typed Racket types, where any type error would be caught at that level.

An interesting aspect of our work is that the support for type expanders was implemented without any change to the core of Typed Racket. Instead, the support for type expanders itself is available as a library, which overrides special forms like define, lambda or cast, enhancing them by pre-processing type expanders, and translating back to the “official” forms from Typed Racket. It is worth noting that Typed Racket itself is implemented in a similar way: special forms like define and lambda support plain type annotations, and translate back to the “official” forms from so-called “untyped” Racket. In both cases, this approach goes with the Racket spirit of implementing languages as libraries (Tobin-Hochstadt et al. 2011)

2.2 Algebraic datatypes for compilers

I used polymorphic variants to solve the assert false problems in my lexical analyser, along with some subtyping. You have to write the typecasts explicitly, but that aside it is very powerful (a constructor can “belong” to several types etc.).
Personal communication from a friend

The phc-adt library implements algebraic datatypes (variants and structures) which are adapted to compiler-writing.

There is an existing “simple” datatype library for Typed Racket (source code available at https://github.com/pnwamk/datatype). It differs from our library on several points:

“datatype” uses nominal typing, while we use structural typing (i.e. two identical type declarations in distinct modules yield the same type in our case). This avoids the need to centralize the type definition of ASTs.
“datatype” uses closed variants, where a constructor can only belong to one variant. We simply define variants as a union of constructors, where a constructor can belong to several variants. This allows later passes in the compiler to add or remove cases of variants, without the need to duplicate all the constructors under slightly different names.
“datatype” does not support row polymorphism, or similarly the update and extension of its product types with values for existing and new fields, regardless of optional fields. We implement the latter.

[Cite the variations on variants paper (for Haskell)]Todo

2.2.1 The case for bounded row polymorphism

[Explain the “expression problem”.]Todo [Talk about the various ways in which it can be “solved”, and which tradeoffs we aim for. Mention extensible-functions, another solution to the expression problem in Racket, but with rather different tradeoffs.]Todo

We strive to implement compilers using many passes. A pass should be able to accept a real-world AST, and produce accordingly a real-world transformed AST as its output. It should also be possible to use lightweight “mock” ASTs, containing only the values relevant to the passes under test (possibly only the pass being called, or multiple passes tested from end to end). The pass should then return a corresponding simplified output AST, omitting the fields which are irrelevant to this pass (and were not part of the input). Since the results of the pass on a real input and on a test input are equivalent modulo the irrelevant fields, this allows testing the pass in isolation with simple data, without having to fill in each irrelevant field with null (and hope that they are indeed irrelevant, without a comforting guarantee that this is the case), as is commonly done when creating “mocks” to test object-oriented programs.

This can be identified as a problem similar to the “expression problem”. In our context, we do not strive to build a compiler which can be extended in an “open world”, by adding new node types to the AST, or new operations handling these nodes. Rather, the desired outcome is to allow passes to support multiple known subsets of the same AST type, from the start.

We succinctly list below some of the different sorts of polymorphism, and argue that row polymorphism is well-suited for our purpose. More specifically, bounded row polymorphism gives the flexibility needed when defining passes which keep some fields intact (without reading their value), but the boundedness ensures that changes in the input type of a pass do not go unnoticed, so that the pass can be amended to handle the new information, or its type can be updated to ignore this new information.

Subtyping, polymorphism and alternatives

(Ducournau 2014). (Cardelli and Wegner 1985)

Subtyping (also called inclusion polymorphism, subtype polymorphism, or nominal subtyping ?): Subclasses and interfaces in C# and Java, sub-structs and union types in Typed Racket, polymorphic variants in CAML (Minsky et al. 2013b), chap. 6, sec. Polymorphic Variants
Multiple inheritance. NIT, CLOS, C++, C# interfaces, Java interfaces. As an extension in “untyped” Racket with Alexis King’s safe multimethods1010 https://lexi-lambda.github.io/blog/2016/02/18/simple-safe-multimethods-in-racket/.
This in principle could help in our case: AST nodes would have .withField(value) methods returning a copy of the node with the field’s value updated, or a node of a different type with that new field, if it is not present in the initial node type. This would however require the declaration of many such methods in advance, so that they can be used when needed (or with a recording mechanism like the one we use, so that between compilations the methods called are remembered and generated on the fly by a macro). Furthermore, Typed Racket lacks support for multiple inheritance on structs. It supports multiple inheritance for classes [?]Todo, but classes currently lack the ability to declare immutable fields, which in turn causes problems with occurrence typing (see the note in the “row polymorphism” point below).
Parametric polymorphism: Generics in C# and Java, polymorphic types in CAML and Typed Racket
F-bounded polymorphism: Java, C#, C++, Eiffel. Possible to mimic to some extent in Typed Racket with (unbounded) parametric polymorphism and intersection types. [Discuss how it would work/not work in our case.]Todo
Operator overloading (also called overloading polymorphism?) and multiple dispatch:
- Operator overloading in C#
- Nothing in Java aside from the built-in cases for arithmetic and string concatenation, but those are not extensible
- C++
- typeclasses in Haskell? [I’m not proficient enough in Haskell to be sure or give a detailed description, I have to ask around to double-check.]Todo
- LISP (CLOS): has multiple dispatch
- nothing built-in in Typed Racket.
- CAML?
Coercion polymorphism (automatic casts to a given type). This includes Scala’s implicits, C# implicit coercion operators (user-extensible, but at most one coercion operator is applied automatically, so if there is a coercion operator A \rightarrow{} B, and a coercion operator B \rightarrow{} C, it is still impossible to supply an A where a C is expected without manually coercing the value), and C++’s implicit conversions, where single-argument constructors are treated as implicit conversion operators, unless annotated with the explicit keyword. Similarly to C#, C++ allows only one implicit conversion, not two or more in a chain.
Struct type properties in untyped Racket can somewhat be used to that effect, although they are closer to Java’s interfaces than to coercion polymorphism. Struct type properties are unsound in Typed Racket and are not represented within the type system, so their use is subject to caution anyway.
Coercion (downcasts). Present in most typed languages. This would not help in our case, as the different AST types are incomparable (especially since Typed Racket lacks multiple inheritance)
Higher-kinded polymorphism: Type which is parameterized by a \mathit{Type} \rightarrow{} \mathit{Type} function. Scala, Haskell. Maybe CAML?
The type expander library which we developed for Typed Racket supports \Lambda{}, used to describe anonymous type-level macros. They enable some limited form of \mathit{Type} \rightarrow{} \mathit{Type} functions, but are actually applied at macro-expansion time, before typechecking is performed, which diminishes their use in some cases. For example, they cannot cooperate with type inference. Also, any recursive use of type-level macros must terminate, unless the type “function” manually falls back to using \mathit{Rec} to create a regular recursive type. This means that a declaration like F(X) := X × F(F(X)) is not possible using anonymous type-level macros only.
As an example of this use of the type expander library, our cycle-handling code uses internally a “type traversal” macro. In the type of a node, it performs a substitution on some subparts of the type. It is more or less a limited form of application of a whole family of type functions a{}_i \rightarrow{} b{}_i, which have the same inputs a{}_i \ldots{}, part of the initial type, but different outputs b{}_i \ldots{} which are substituted in place of the a{}_i \ldots{} in the resulting type. The “type traversal” macro expands the initial type into a standard polymorphic type, which accepts the desired outputs b{}_i \ldots{} as type arguments.
Lenses. Can be in a way compared to explicit coercions, where the coercion is reversible and the accessible parts can be altered.
Structural polymorphism (also sometimes called static duck-typing): Scala, TypeScript. It is also possible in Typed Racket, using the algebraic datatypes library which we implemented. Possible to mimic in Java and C# with interfaces “selecting” the desired fields, but the interface has to be explicitly implemented by the class (i.e. at the definition site, not at the use-site).
Palmer et al. present TinyBang (Palmer et al. 2014), a typed language in which flexible manipulation of objects is possible, including adding and removing fields, as well as changing the type of a field. They implement in this way a sound, decidable form of static duck typing, with functional updates which can add new fields and replace the value of existing fields. Their approach is based on two main aspects:
- Type-indexed records supporting asymmetric concatenation: by concatenating two records r{}_1 \& r{}_2, a new record is obtained containing all the fields from r{}_1 (associated to their value in r{}_1), as well as the fields from r{}_2 which do not appear in r{}_1 (associated to their value in r{}_2). Primitive types are eliminated by allowing the use of type names as keys in the records: integers then become simply records with a int key, for example.
- Dependently-typed first-class cases: pattern-matching functions are expressed as pattern \mathbin{\texttt{->}} expression, and can be concatenated with the \& operator, to obtain functions matching against different cases, possibly with a different result type for each case. The leftmost cases can shadow existing cases (i.e. the case which is used is the leftmost case for which the pattern matches successfully).
TinyBang uses an approach which is very different from the one we followed in our Algebraic Data Types library, but contains the adequate primitives to build algebraic data types which would fulfill our requirements (aside from the ability to bound the set of extra “row” fields). We note that our flexible structs, which are used within the body of node-to-node functions in passes, do support an extension operation, which is similar to TinyBang’s \&, with the left-hand side containing a constant and fixed set of fields.
Row polymorphism: Apparently, quoting a post on Quora1111 https://www.quora.com/Object-Oriented-Programming-What-is-a-concise-definition-of-polymorphism\label{quora-url-footnote}:
Mostly only concatenative and functional languages (like Elm and PureScript) support this.
Classes in Typed Racket can have a row type argument (but classes in Typed Racket cannot have immutable fields (yet), and therefore occurrence typing does not work on class fields. Occurrence typing is an important idiom in Typed Racket, used to achieve safe but concise pattern-matching, which is a feature frequently used when writing compilers).
Our Algebraic Data Types library implements a bounded form of row polymorphism, and a separate implementation (used within the body of node-to-node functions in passes) allows unbounded row polymorphism.
[Virtual types]Todo
So-called “untyped” or “uni-typed” languages: naturally support most of the above, but without static checks.
Operator overloading can be present in “untyped” languages, but is really an incarnation of single or multiple dispatch, based on the run-time, dynamic type (as there is no static type based on which the operation could be chosen). However it is not possible in “untyped” languages and languages compiled with type erasure to dispatch on “types” with a non-empty intersection: it is impossible to distinguish the values, and they are not annotated statically with a type.
As mentioned above, Typed Racket does not have operator overloading, and since the inferred types cannot be accessed reflectively at compile-time, it is not really possible to construct it as a compile-time feature via macros. Typed Racket also uses type erasure, so the same limitation as for untyped languages applies when implementing some form of single or multiple dispatch at run-time — namely the intersection of the types must be empty. [Here, mention (and explain in more detail later) our compile-time “empty-intersection check” feature (does not work with polymorphic variables).]Todo

[Overview of the existing “solutions” to the expression problems, make a summary table of their tradeoffs (verbosity, weaknesses, strengths).]Todo

[Compare the various sorts of subtyping and polymorphism in that light (possibly in the same table), even those which do not directly pose as a solution to the expression problem.]Todo

“Nominal types”: our tagged structures and node types are not nominal types.

The “trivial” Racket library tracks static information about the types in simple cases. The “turnstile” Racket language [is a follow-up]Todo work, and allows to define new typed Racket languages. It tracks the types of values, as they are assigned to variables or passed as arguments to functions or macros. These libraries could be used to implement operator overloads which are based on the static type of the arguments. It could also be used to implement unbounded row polymorphism in a way that does not cause a combinatorial explosion of the size of the expanded code.[Have a look at the implementation of row polymorphism in Typed Racket classes, cite their work if there is something already published about it.]Todo

From the literate program (tagged-structure-low-level):

Row polymorphism, also known as "static duck typing" is a type system feature which allows a single type variable to be used as a place holder for several omitted fields, along with their types. The phc-adt library supports a limited form of row polymorphism: for most operations, a set of tuples of omitted field names must be specified, thereby indicating a bound on the row type variable.
This is both a limitation of our implementation (to reduce the combinatorial explosion of possible input and output types), as well as a desirable feature. Indeed, this library is intended to be used to write compilers, and a compiler pass should have precise knowledge of the intermediate representation it manipulates. It is possible that a compiler pass may operate on several similar intermediate representations (for example a full-blown representation for actual compilation and a minimal representation for testing purposes), which makes row polymorphism desirable. It is however risky to allow as an input to a compiler pass any data structure containing at least the minimum set of required fields: changes in the intermediate representation may add new fields which should, semantically, be handled by the compiler pass. A catch-all row type variable would simply ignore the extra fields, without raising an error. Thanks to the bound which specifies the possible tuples of omitted field names, changes to the the input type will raise a type error, bringing the programmer’s attention to the issue. If the new type is legit, and does not warrant a modification of the pass, the fix is easy to implement: simply adding a new tuple of possibly omitted fields to the bound (or replacing an existing tuple) will allow the pass to work with the new type. If, on the other hand, the pass needs to be modified, the type system will have successfully caught a potential issue.

2.3 Writing compilers using many small passes (a.k.a following the Nanopass Compiler Framework philosophy)

2.4 Cycles in intermediate representations of programs

[There already were a few references in my proposal for JFLA.]Todo [Look for articles about graph rewriting systems.]Todo

The following sections present the many ways in which cycles within the AST, CFG and other intermediate representations can be represented.

2.4.1 Mutable data structures

Hard to debug
When e.g. using lazy-loading, it is easy to mistakenly load a class or method after the Intermediate Representation was frozen. Furthermore, unless a .freeze() method actually enforces this conceptual change from a mutable to an immutable representation, it can be unclear at which point the IR (or parts of it) is guaranteed to be complete and its state frozen. This is another factor making maintenance of such code difficult.

Quote from (Ramsey and Dias 2006):

We are using ML to build a compiler that does low-level optimization. To support optimizations in classic imperative style, we built a control-flow graph using mutable pointers and other mutable state in the nodes. This decision proved unfortunate: the mutable flow graph was big and complex, and it led to many bugs. We have replaced it by a smaller, simpler, applicative flow graph based on Huet’s (1997) zipper. The new flow graph is a success; this paper presents its design and shows how it leads to a gratifyingly simple implementation of the dataflow framework developed by Lerner, Grove, and Chambers (2002).

2.4.2 Unique identifiers used as a replacement for pointers

Mono uses that (Evain and others 2008; Köplinger et al. 2014), it is very easy to use an identifier which is supposed to reference a missing object, or an object from another version of the AST. It is also very easy to get things wrong when duplicating nodes (e.g. while specializing methods based on their caller), or when merging or removing nodes.

2.4.3 Explicit use of other common graph representations

Adjacency lists, De Bruijn indices.

Error prone when updating the graph (moving nodes around, adding, duplicating or removing nodes).
Needs manual

2.4.4 Using lazy programming languages

Lazy programming is harder to debug.
Quote (Nilsson and Fritzson 1993):
Traditional debugging techniques are, however, not suited for lazy functional languages since computations generally do not take place in the order one might expect.
Quote (Nilsson and Fritzson 1993):
Within the field of lazy functional programming, the lack of suitable debugging tools has been apparent for quite some time. We feel that traditional debugging techniques (e.g. breakpoints, tracing, variable watching etc.) are not particularly well suited for the class of lazy languages since computations in a program generally do not take place in the order one might expect from reading the source code.
Quote (Wadler 1998):
To be usable, a language system must be accompanied by a debugger and a profiler. Just as with interlanguage working, designing such tools is straightforward for strict languages, but trickier for lazy languages.
Quote (Wadler 1998):
Constructing debuggers and profilers for lazy languages is recognized as difficult. Fortunately, there have been great strides in profiler research, and most implementations of Haskell are now accompanied by usable time and space profiling tools. But the slow rate of progress on debuggers for lazy languages makes us researchers look, well, lazy.
Quote (Morris 1982):
How does one debug a program with a surprising evaluation order? Our attempts to debug programs submitted to the lazy implementation have been quite entertaining. The only thing in our experience to resemble it was debugging a multi-programming system, but in this case virtually every parameter to a procedure represents a new process. It was difficult to predict when something was going to happen; the best strategy seems to be to print out well-defined intermediate results, clearly labelled.
So-called “infinite” data structures constructed lazily have problems with equality and serialization. The latter is especially important for serializing and de-serializing Intermediate Representations for the purpose of testing, and is also very important for code generation: the backend effectively needs to turn the infinite data structure into a finite one. The Revised$^6$ Report on Scheme requires the "equal?" predicate to correctly handle cyclic data structures, but efficient algorithms implementing this requirement are nontrivial (Adams and Dybvig 2008). Although any representation of cyclic data structures will have at some point to deal with equality and serialization, it is best if these concerns are abstracted away as much as possible.

2.4.5 True graph representations using immutable data structures

Roslyn (Overbey 2013) : immutable trees with “up” pointers
The huet zipper (Huet 1997). Implementation in untyped Racket, but not Typed Racket1212 See zippers, and https://github.com/david-christiansen/racket-zippers

3 Goals, constraints and examples

\def\ifmathjax#1{#1}\def\iflatex#1{}

4 Typed Racket

\def\ifmathjax#1{#1}\def\iflatex#1{}

We start this section with some history: Lisp, the language with lots of parentheses, shortly following Fortran as one of the first high-level programming languages, was initially designed between 1956 and 1958, and subsequently implemented (McCarthy 1981). Dialects of Lisp generally support a variety of programming paradigms, including (but not limited to) functional programming and object-oriented programming (e.g. via CLOS, the Common Lisp Object System). One of the the most proeminent aspects of Lisp is homoiconicity, the fact that programs and data structures look the same. This enables programs to easily manipulate other programs, and led to the extensive use of macros. Uses of macros usually look like function applications, but, instead of invoking a target function at run-time, a macro will perform some computation at compile-time, and expand to some new code, which is injected as a replacement of the macro’s use.

The two main dialects of Lisp are Common Lisp and Scheme. Scheme follows a minimalist philosophy, where a small core is standardised (Abelson et al. 1998; Shinn et al. 2013; Sperber et al. 2009) and subsequently extended via macros and additional function definitions.

Racket, formerly named PLT Scheme, started as a Scheme implementation. Racket evolved, and the Racket Manifesto (Felleisen et al. 2015) presents it as a “programming-language programming language”, a language which helps with the creation of small linguistic extensions as well as entirely new languages. The Racket ecosystem features many languages covering many paradigms:

The racket/base language is a full-featured programming language which mostly encourages functional programming.
racket/class implements an object-oriented system, implemented atop racket/base using macros, and can be used along with the rest of the racket/base language.
racklog is a logic programming language in the style of prolog. The Racket ecosystem also includes an implementation of datalog.
Scribble can be seen as an alternative to LaTeX, and is used to create the Racket documentation. It also supports literate programming, by embedding chunks of code in the document which are then aggregated together. This thesis is in fact written using Scribble.
slideshow is a DSL (domain-specific language) for the creation of presentations, and can be thought as an alternative to Beamer and SliTeX.
r5rs and r6rs are implementations of the corresponding scheme standards.
Redex is a DSL which allows the specification of reduction semantics for programming languages. It features tools to explore and test the defined semantics.
Typed Racket (Tobin-Hochstadt 2010; Tobin-Hochstadt and Felleisen 2008) is a typed variant of the main racket language. It is implemented as a macro which takes over the whole body of the program. That macro fully expands all other macros in the program, and then typechecks the expanded program.
Turnstile allows the creation of new typed languages. It takes a different approach when compared to Typed Racket, and threads the type information through assignments and special forms, in order to be able to typecheck the program during expansion, instead of doing so afterwards.

In the remainder of this section, we will present the features of Typed Racket’s type system, and then present formal semantics for a subset of those, namely the part which is relevant to our work. The Typed Racket Guide and The Typed Racket Reference provide good documentation for programmers who desire to use Typed Racket; we will therefore keep our overview succinct and gloss over most details.

4.1 Overview of Typed Racket’s type system

4.1.1 Simple primitive types

Typed Racket has types matching Racket’s baggage of primitive values: Number, Boolean, Char, String, Void1313 The Void type contains only a single value, #<void>, and is equivalent to the void type in C. It is the equivalent of unit of CAML and Haskell, and is often used as the return type of functions which perform side-effects. It should not be confused with Nothing, the bottom type which is not inhabited by any value, and is similar to the type of Haskell’s undefined. Nothing can be used for example as the type of functions which never return — in that way it is similar to C’s __attribute__ ((__noreturn__)). and so on.

> (ann #true Boolean)
- : Boolean
#t
> 243
- : Integer [more precisely: Positive-Byte]
243
> "Hello world"
- : String
"Hello world"
> #\c
- : Char
#\c
; The void function produces the void value
; Void values on their own are not printed,
; so we place it in a list to make it visible.
> (list (void))
- : (Listof Void) [more precisely: (List Void)]
'(#<void>)

For numbers, Typed Racket offers a “numeric tower” of partially-overlapping types: Positive-Integer is a subtype of Integer, which is itself a subtype of Number. Zero, the type containing only the number 0, is a both a subtype of Nonnegative-Integer (numbers ≥ 0) and of Nonpositive-Integer (numbers ≤ 0).

Typed Racket also includes a singleton type for each primitive value of these types: we already mentioned Zero, which is an alias of the 0 type. Every number, character, string and boolean value can be used as a type, which is only inhabited by the same number, character, string or boolean value. For example, 243 belongs to the singleton type 243, which is a subtype of Positive-Integer.

> 0
- : Integer [more precisely: Zero]
0
> (ann 243 243)
- : Integer [more precisely: 243]
243
> #t
- : Boolean [more precisely: True]
#t

4.1.2 Pairs and lists

Pairs are the central data structure of most Lisp dialects. They are used to build linked lists of pairs, terminated by '(), the null element. The null element has the type Null, while the pairs which build the list have the type (Pairof A B), where A and B are replaced by the actual types for the first and second elements of the pair. For example, the pair built using (cons 729 #true), which contains 729 as its first element, and #true as its second element, has the type (Pairof Number Boolean), or using the most precise singleton types, (Pairof 729 #true).

> (cons 729 #true)
- : (Pairof Positive-Index True)
'(729 . #t)
> '(729 . #true)
- : (Pairof Positive-Index True)
'(729 . #t)

Heterogeneous linked lists of fixed length can be given a precise type by nesting the same number of pairs at the type level. For example, the list built with (list 81 #true 'hello) has the type (List Number Boolean Symbol), which is a shorthand for the type (Pairof Number (Pairof Boolean (Pairof Symbol Null))). Lists in Typed Racket can thus be seen as the equivalent of a chain of nested 2-tuples in languages like CAML or Haskell. The analog in object-oriented languages with support for generics would be a class Pair<A, B>, where the generic type argument B could be instantiated by another instance of Pair, and so on.

> (cons 81 (cons #true (cons 'hello null)))
- : (Listof (U 'hello Positive-Byte True))
'(81 #t hello)
> (ann (list 81 #true 'hello)
(Pairof Number (Pairof Boolean (Pairof Symbol Null))))
- : (Listof (U Boolean Complex Symbol)) [more precisely: (List Number Boolean Symbol)]
'(81 #t hello)

The type of variable-length homogeneous linked lists can be described using the Listof type operator. The type (Listof Integer) is equivalent to (Rec R (U (Pairof Integer R) Null)). The Rec type operator describes recursive types, and U describes unions. Both of these features are described below, for now we will simply say that the previously given type is a recursive type R, which can be a (Pairof Integer R) or Null (to terminate the linked list).

> (ann (range 0 5) (Listof Number))
- : (Listof Number)
'(0 1 2 3 4)

4.1.3 Symbols

Another of Racket’s primitive datatypes is symbols. Symbols are interned strings: two occurrences of a symbol produce values which are pointer-equal if the symbols are equal (i.e. they represent the same string)1414 This is true with the exception of symbols created with gensym and the like. gensym produces a fresh symbol which is not interned, and therefore different from all existing symbols, and different from all symbols created in the future..

Typed Racket includes the Symbol type, to which all symbols belong. Additionally, there is a singleton type for each symbol: the type 'foo is only inhabited by the symbol 'foo.

> 'foo
- : Symbol [more precisely: 'foo]
'foo

Singleton types containing symbols can be seen as similar to constructors without arguments in CAML and Haskell, and as globally unique enum values in object-oriented languages. The main difference resides in the scope of the declaration: two constructor declarations with identical names in two separate files will usually give distinct types and values. Similarly, when using the “type-safe enum” design pattern, two otherwise identical declarations of an enum will yield objects of different types. In contrast, two uses of an interned symbols in Racket and Typed Racket will produce identical values and types. A way of seeing this is that symbols are similar to constructors (in the functional programming sense) or enums which are implicitly declared globally.

> (module m1 typed/racket
    (define sym1 'foo)
    (provide sym1))
> (module m2 typed/racket
    (define sym2 'foo)
    (provide sym2))
> (require 'm1 'm2)
; The tow independent uses of 'foo are identical:
> (eq? sym1 sym2)
- : Boolean
#t

4.1.4 Unions

These singleton types may not seem very useful on their own. They can however be combined together with union types, which are built using the U type operator.

The union type (U 0 1 2) is inhabited by the values 0, 1 and 2, and by no other value. The Boolean type is actually defined as (U #true #false), i.e. the union of the singleton types containing the #true and #false values, respectively. The Nothing type, which is not inhabited by any value, is defined as the empty union (U). The type Any is the top type, i.e. it is a super-type of all other types, and can be seen as a large union including all other types, including those which will be declared later or in other units of code.

Unions of symbols are similar to variants which contain zero-argument constructors, in CAML or Haskell.

> (define v : (U 'foo 'bar) 'foo)
> v
- : Symbol [more precisely: (U 'bar 'foo)]
'foo
> (set! v 'bar)
> v
- : Symbol [more precisely: (U 'bar 'foo)]
'bar
; This throws an error at compile-time:
> (set! v 'oops)
eval:5:0: Type Checker: type mismatch;
mutation only allowed with compatible types
  expected: (U 'bar 'foo)
  given: 'oops
  in: oops

A union such as (U 'ca (List 'cb Number) (List 'cc String Symbol)) can be seen as roughly the equivalent of a variant with three constructors, ca, cb and cc, where the first has no arguments, the second has one argument (a Number), and the third has two arguments (a String and a Symbol).

The main difference is that a symbol can be used as parts of several unions, e.g. (U 'a 'b) and (U 'b 'c), while constructors can often only be part of the variant used to declare them. Unions of symbols are in this sense closer to CAML’s so-called polymorphic variants (Minsky et al. 2013a) than to regular variants.

> (define-type my-variant (U 'ca
(List 'cb Number)
(List 'cc String Symbol)))
> (define v₁ : my-variant 'ca)
> (define v₂ : my-variant (list 'cb 2187))
> (define v3 : my-variant (list 'cc "Hello" 'world))

Finally, it is possible to mix different sorts of types within the same union: the type (U 0 #true 'other) is inhabited by the number 0, the boolean #true, and the symbol 'other. Translating such an union to a language like CAML could be done by explicitly tagging each case of the union with a distinct constructor.

Implementation-wise, all values in the so-called “untyped” version of Racket are tagged: a few bits within the value’s representation are reserved and used to encode the value’s type. When considering the target of a pointer in memory, Racket is therefore able to determine if the pointed-to value is a number, boolean, string, symbol and so on. Typed Racket preserves these run-time tags. They can then be used to detect the concrete type of a value when its static type is a union. This detection is done simply by using Racket’s predicates: number?, string?, symbol? etc.

4.1.5 Intersections

Intersections are the converse of unions: instead of allowing a mixture of values of different types, an intersection type, described using the ∩ type operator, only allows values which belong to all types.

The intersection type (∩ Nonnegative-Integer Nonpositive-Integer) is the singleton type 0. The intersection of (U 'a 'b 'c) and (U 'b 'c 'd) will be (U 'b 'c), as 'b and 'c belong to both unions.

; :type shows the given type, or a simplified version of it
> (:type (∩ (U 'a 'b 'c) (U 'b 'c 'd)))
(U 'b 'c)

Typed Racket is able to reduce some intersections such as those given above at compile-time. However, in some cases, it is forced to keep the intersection type as-is. For example, structs (describled below can, using special properties, impersonate functions. This mechanism is similar to PHP’s __invoke, the ability to overload operator() in C++. Typed Racket does not handle these properties (yet), and therefore cannot determine whether a given struct type also impersonates a function or not. This means that the intersection (∩ s (→ Number String)), where s is a struct type, cannot be reduced to Nothing, because Typed Racket cannot determine whether the struct s can act as a function or not.

Another situation where Typed Racket cannot reduce the intersection is when intersecting two function types (presented below).

(∩ (→ Number String) (→ Number Symbol))
(∩ (→ Number String) (→ Boolean String))

The first intersection seems like could be simplified to (→ Number String) (→ Number Symbol), and the second one could be simplified to (→ (U Number Boolean) String), however the equivalence between these types has not been implemented (yet) in Typed Racket, so we do not rely on them. Note that this issue is not a soundness issue: it only prevents passing values types to which they belong in principle, but it cannot be exploited to assign a value to a variable with an incompatible type.

Finally, when some types are intersected with a polymorphic type variable, the intersection cannot be computed until the polymorphic type is instantiated.

When Typed Racket is able to perform a simplification, occurrences of Nothing (the bottom type) propagate outwards in some cases, pairs and struct types which contain Nothing as one of their elements being collapsed to Nothing. This propagation of Nothing starts from occurrences of Nothing in the parts of the resulting type which are traversed by the intersection operator. It collapses the containing pairs and struct types to Nothing, moving outwards until the ∩ operator itself is reached. In principle, the propagation could go on past that point, but this is not implemented yet in Typed Racket1515 See Issue #552 on Typed Racket’s GitHub repository for more details on what prevents implementing a more aggressive propagation of Nothing..

The type (∩ 'a 'b) therefore gets simplified to Nothing, and the type (∩ (Pairof 'a 'x) (Pairof 'b 'x)) also simplifies to Nothing (Typed Racket initially pushes the intersection down the pairs, so that the type first becomes (Pairof (∩ 'a 'b) (∩ 'x 'x)), which is simplified to (Pairof Nothing 'x), and the occurrence of Nothing propagates outwards). However, if the user directly specifies the type (Pairof (∩ 'a 'b) Integer), it is simplified to (Pairof Nothing Integer), but the Nothing does not propagate outwards beyond the initial use of ∩.

> (:type (∩ 'a 'b))
Nothing
> (:type (∩ (Pairof 'a 'x) (Pairof 'b 'x)))
Nothing
> (:type (Pairof (∩ 'a 'b) Integer))
(Pairof Nothing Integer)
[can expand further: Integer]

A simple workaround exists: the outer type, which could be collapsed to Nothing, can be intersected again with a type of the same shape. The outer intersection will traverse both types (the desired one and the “shape”), and propagate the leftover Nothing further out.

> (:type (Pairof (∩ 'a 'b) Integer))
(Pairof Nothing Integer)
[can expand further: Integer]
> (:type (∩ (Pairof (∩ 'a 'b) Integer)
(Pairof Any Any)))
Nothing

These intersections are not very interesting on their own, as in most cases it is possible to express the resulting simplified type without using the intersection operator. They become more useful when mixed with polymorphic types: intersecting a polymorphic type variable with another type can be used to restrict the actual values that may be used. The type (∩ A T), where A is a polymorphic type variable and T is a type defined elsewhere, is equivalent to the use of bounded type parameters in Java or C#. In C#, for example, the type (∩ A T) would be written using an where A : T clause.

4.1.6 Structs

Racket also supports structs, which are mappings from fields to values. A struct is further distinguished by its struct type: instances of two struct types with the same name and fields, declared in separate files, can be differentiated using the predicates associated with these structs. Structs in Racket can be seen as the analog of classes containing only fields (but no methods) in C# or Java. Such classes are sometimes called “Plain Old Data (POD) Objects”. Structs belong to a single-inheritance hierarchy: instances of the descendents of a struct type are recognised by their ancestor’s predicate. When a struct inherits from another, it includes its parent’s fields, and can add extra fields of its own.

Each struct declaration within a Typed Racket program additionally declares corresponding type.

> (struct parent ([field₁ : (Pairof String Symbol)])
    #:transparent)
> (struct s parent ([field₂ : Integer]
                    [field₃ : Symbol])
    #:transparent)
> (s (cons "x" 'y) 123 'z)
- : s
(s '("x" . y) 123 'z)

In Typed Racket, structs can have polymorphic type arguments, which can be used inside the types of the struct’s fields.

> (struct (A B) poly-s ([field₁ : (Pairof A B)]
                        [field₂ : Integer]
                        [field₃ : B])
    #:transparent)
> (poly-s (cons "x" 'y) 123 'z)
- : (poly-s String (U 'y 'z))
(poly-s '("x" . y) 123 'z)

Racket further supports struct type properties, which can be seen as a limited form of method definitions for a struct, thereby making them closer to real objects. The same struct type property can be implemented by many structs, and the declaration of a struct type property is therefore roughly equivalent to the declaration of an interface with a single method.

Struct type properties are often considered a low-level mechanism in Racket. Among other things, a struct type property can only be used to define a single property at a time. When multiple “methods” have to be defined at once (for example, when defining the prop:equal+hash property, which requires the definition of an equality comparison function, and two hashing functions), these can be grouped together in a list of functions, which is then used as the property’s value. “Generic interfaces” are a higher-level feature, which among other things allow the definition of multiple “methods” as part of a single generic interface, and offers a friendlier API for specifying the “generic interface” itself (i.e. what Object Oriented languages call an interfece), as and for specifying the implementation of said interface.

Typed Racket unfortunately offers no support for struct type properties and generic interfaces for now. It is impossible to assert that a struct implements a given property at the type level, and it is also for example not possible to describe the type of a function accepting any struct implementing a given property or generic interface. Finally, no type checks are performed on the body of functions bound to such properties, and to check verifies that a function implementation with the right signature is supplied to a given property. Since struct type properties and generics cannot be used in a type-safe way for now, we refrain from using these features, and only use them to implement some very common properties1616 We built a thin macro wrapper which allows typechecking the implementation and signature of the functions bound to these two properties.: prop:custom-write which is the equivalent of Java’s void toString(), and prop:equal+hash which is equivalent to Java’s boolean equals(Object o) and int hashCode().

4.1.7 Functions

Typed Racket provides rich function types, to support some of the flexible use patterns allowed by Racket.

The simple function type below indicates that the function expects two arguments (an integer and a string), and returns a boolean:

(→ Integer String Boolean)

We note that unlike Haskell and CAML functions, Racket functions are not implicitly curried. To express the corresponding curried function type, one would write:

(→ Integer (→ String Boolean))

A function may additionally accept optional positional arguments, and keyword (i.e. named) arguments, both mandatory and optional:

; Mandatory string, optional integer and boolean arguments:
(->* (String) (Integer Boolean) Boolean)
; Mandatory keyword arguments:
(→ #:size Integer #:str String Boolean)
; Mandatory #:str, optional #:size and #:opt:
(->* (#:str String) (#:size Integer #:opt Boolean) Boolean)

Furthermore, functions in Racket accept a catch-all “rest” argument, which allows for the definition of variadic functions. Typed racket also allows expressing this at the type level, as long as the arguments covered by the “rest” clause all have the same type:

; The function accepts one integer and any number of strings:
(-> Integer String * Boolean)
; Same thing with an optional symbol inbetween:
(->* (Integer) (Symbol) #:rest String Boolean)

One of Typed Racket’s main goals is to be able to typecheck idiomatic Racket programs. Such programs may include functions whose return type depends on the values of the input arguments. Similarly, case-lambda can be used to create lambda functions which dispatch to multiple behaviours based on the number of arguments passed to the function.

Typed Racket provides the case→ type operator, which can be used to describe the type of these functions:

; Allows 1 or 3 arguments, with the same return type.
(case→ (→ Integer Boolean)
       (→ Integer String Symbol Boolean))
; A similar type based on optional arguments allows 1, 2 or 3
; arguments in contrast:
(->* (Integer) (String Symbol) Boolean)
; The output type can depend on the input type:
(case→ (→ Integer Boolean)
       (→ String Symbol))
; Both features (arity and dependent output type) can be mixed
(case→ (→ Integer Boolean)
       (→ Integer String (Listof Boolean)))

Another important feature, which can be found in the type system of most functional programming languages, and most object-oriented languages, is parametric polymorphism. Typed Racket allows the definition of polymorphic structs, as detailed above, as well as polymorphic functions. For example, the function cons can be considered as a polymorphic function with two polymorphic type arguments A and B, which takes an argument of type A, an argument of type B, and returns a pair of A and B.

(∀ (A B) (→ A B (Pairof A B)))

Typed Racket supports polymorphic functions with multiple polymorphic type variables, as the one shown above. Furthermore, it allows one of the polymorphic variables to be followed by ellipses, indicating a variable-arity polymorphic type (Tobin-Hochstadt 2010). The dotted polymorphic type variable can be instantiated with a tuple of types, and will be replaced with that tuple where it appears. For example, the type

(∀ (A B ...) (→ (List A A B ...) Void))

can be instantiated with Number String Boolean, which would yield the type for a function accepting a list of four elements: two numbers, a string and a boolean.

(→ (List Number Number String Boolean) Void)

Dotted polymorphic type variables can only appear in some places. A dotted type variable can be used as the tail of a List type, so (List Number B ...) (a String followed by any number of Bs) is a valid type, but (List B ... String) (any number of Bs followed by a String) is not. A dotted type variable can also be used to describe the type of a variadic function, as long as it appears after all other arguments, so (→ String B ... Void) (a function taking a String, any number of Bs, and returning Void) is a valid type, but (→ String B ... Void) (a function taking any number of Bs, and a String, and returning Void) is not. Finally, a dotted type variable can be used to represent the last element of the tuple of returned values, for functions which return multiple values (which are described below).

When the context makes it unclear whether an ellipsis \ldots{} indicates a dotted type variable, or is used to indicate a metasyntactic repetition at the level of mathematical formulas, we will write the first using τ{}_1 \ldots{} τ{}_n, explicitly indicating the first and last elements, or using \overline{τ} [and we will write the second using \textit{tvar}\ \textit{ooo}]Todo

Functions in Racket can return one or several values. When the number of values returned is different from one, the result tuple can be destructured using special functions such as (call-with-values f g), which passes each value returned by f as a distinct argument to g. The special form (let-values ([(v₁ … vₙ) e]) body) binds each value returned by e to the corresponding vᵢ (the expression e must produce exactly n values). The type of a function returning multiple values can be expressed using the following notation:

(→ In₁ … Inₙ (Values Out₁ … Outₘ))

Finally, predicates (functions whose results can be interpreted as booleans) can be used to gain information about the type of their argument, depending on the result. The type of a predicate can include positive and negative filters, indicated with #:+ and #:-, respectively. The type of the string? predicate is:

(→ Any Boolean : #:+ String #:- (! String))

In this notation, the positive filter #:+ String indicates that when the predicate returns #true, the argument is known to be a String. Conversely, when the predicate exits with #false, the negative filter #:- (! String) indicates that the input could not (!) possibly have been a string. The information gained this way allows regular conditionals based on arbitrary predicates to work like pattern-matching:

> (define (f [x : (U String Number Symbol)])
    (if (string? x)
        ; x is known to be a String here:
        (ann x String)
        ; x is known to be a Number or a Symbol here:
        (ann x (U Number Symbol))))

The propositions do not necessarily need to refer to the value as a whole, and can instead give information about a sub-part of the value. Right now, the user interface for specifying paths can only target the left and right members of cons pairs, recursively. Internally, Typed Racket supports richer paths, and the type inference can produce filters which give information about individual structure fields, or about the result of forced promises, for example.

4.1.8 Occurrence typing

Typed Racket is built atop Racket, which does not natively support pattern matching. Instead, pattern matching forms are implemented as macros, and expand to nested uses of if.

As a result, Typed Racket needs to typecheck code with the following structure:

(λ ([v : (U Number String)])
  (if (string? v)
      (string-append v ".")
      (+ v 1)))

In this short example, the type of v is a union type including Number and String. After applying the string? predicate, the type of v is narrowed down to String in the then branch, and it is narrowed down to Number in the else branch. The type information gained thanks to the predicate comes from the filter part of the predicate’s type (as explained in Functions).

Occurrence typing only works on immutable variables and values. Indeed, if the variable is modified with set!, or if the subpart of the value stored within which is targeted by the predicate is mutable, it is possible for that value to change between the moment the predicate is executed, and the moment when the value is actually used. This places a strong incentive to mostly use immutable variables and values in Typed Racket programs, so that pattern-matching and other forms work well.

In principle, it is always possible to copy the contents of a mutated variable to a temporary one (or copy a mutable subpart of the value to a new temporary variable), and use the predicate on that temporary copy. The code in the then and else branches should also use the temporary copy, to benefit from the typing information gained via the predicate. In our experience, however, it seems that most macros which perform tasks similar to pattern-matching do not provide an easy means to achieve this copy. It therefore remains more practical to avoid mutation altogether when possible.

4.1.9 Recursive types

Typed Racket allows recursive types, both via (possibly mutually-recursive) named declarations, and via the Rec type operator.

In the following examples, the types Foo and Bar are mutually recursive. The type Foo matches lists with an even number of alternating Integer and String elements, starting with an Integer,

(define-type Foo (Pairof Integer Bar))
(define-type Bar (Pairof String (U Foo Null)))

This same type could alternatively be defined using the Rec operator. The notation (Rec R T) builds the type T, where occurrences of R are interpreted as recursive occurrences of T itself.

(Rec R
     (Pairof Integer
             (Pairof String
                     (U R Null))))

4.1.10 Classes

The racket/class module provides an object-oriented system for Racket. It supports the definition of a hierarchy of classes with single inheritance, interfaces with multiple inheritance, mixins and traits (methods and fields which may be injected at compile-time into other classes), method renaming, and other features.

The typed/racket/class module makes most of the features of racket/class available to Typed Racket. In particular, it defines the following type operators:

Class is used to describe the features a class, including the signature of its constructor, as well as the public fields and methods exposed by the class. We will note that a type expressed with Class does not mention the name of the class. Any concrete implementation which exposes all (and only) the required methods, fields and constructor will inhabit the type. In other words, the types built with Class are structural, and not nominal.
Object is used to describe the methods and fields which an already-built object bears.
The (Instance (Class …)) type is a shorthand for the Object type of instances of the given class type. It can be useful to describe the type of an instance of a class without repeating all the fields and methods (which could have been declared elsewhere).

In types described using Class and Instance, it is possible to omit fields which are not relevant. These fields get grouped under a single row polymorphic type variable. A row polymorphic function can, for example, accept a class with some existing fields, and produce a new class extending the existing one:

> (: add-my-field (∀ (r #:row)
                     (-> (Class (field [existing Number])
                                #:row-var r)
                         (Class (field [existing Number]
                                       [my-field String])
                                #:row-var r))))
> (define (add-my-field parent%)
    (class parent%
      (super-new)
      (field [my-field : String "Hello"])))

The small snippet of code above defined a function add-my-field which accepts a parent% class exporting at least the existing field (and possibly other fields and methods). It then creates an returns a subclass of the given parent% class, extended with the my-field field.

We consider the following class, with the required existing field, and a supplementary other field:

> (define a-class%
    (class object%
      (super-new)
      (field [existing : Integer 0]
             [other : Boolean #true])))

When passed to the add-my-field function, the row type variable is implicitly instantiated with the field [other Boolean]. The result of that function call is therefore a class with the three fields existing, my-field and other.

> (add-my-field a-class%)
- : (Class (field (existing Number) (my-field String) (other Boolean)))
#<class:add-my-field>

These mechanisms can be used to perform reflective operations on classes like adding new fields and methods to dynamically-created subclasses, in a type-safe fashion.

The Row operator can be used along with row-inst to explicitly instantiate a row type variable to a specific set of fields and methods. The following call to add-my-field is equivalent to the preceding one, but does not rely on the automatic inference of the row type variable.

> ({row-inst add-my-field (Row (field [other Boolean]))} a-class%)
- : (Class (field (existing Number) (my-field String) (other Boolean)))
#<class:add-my-field>

We will not further describe this object system here, as our work does not rely on this aspect of Typed Racket’s type system. We invite the curious reader to refer to the documentation for racket/class and typed/racket/class for more details.

We will simply note one feature which is so far missing from Typed Racket’s object system: immutability. It is not possible yet to indicate in the type of a class that a field is immutable, or that a method is pure (in the sense of always returning the same value given the same input arguments). The absence of immutability means that occurrence typing does not work on fields. After testing the value of a field against a predicate, it is not possible to narrow the type of that field, because it could be mutated by a third party between the check and future uses of the field.

4.1.11 Local type inference

Unlike many other statically typed functional languages, Typed Racket does not rely on a Hindley–Milner type system (Hindley 1969; Milner 1978). This choice was made for several reasons (Tobin-Hochstadt 2010):

Typed Racket’s type system is rich and contains many features. Among other things, it mixes polymorphism and subtyping, which notoriously make typechecking difficult.
The authors of Typed Racket claim that global type inference often produces indecipherable error messages, with a small change having repercussions on the type of terms located in other distant parts of the program.
The authors of Typed Racket suggest that type annotations are often beneficial as documentation. Since the type annotations are checked at compile-time, they additionally will stay synchronised with the code that they describe, and will not become out of date.

Instead of relying on global type inference, Typed Racket uses local type inference to determine the type of local variables and expressions. Typed Racket’s type inference can also determine the correct instantiation for most calls to polymorphic functions. It however requires type annotations in some places. For example, it is usually necessary to indicate the type of the parameters when defining a function.

4.2 Formal semantics for part of Typed Racket’s type system

\def\ifmathjax#1{#1}\def\iflatex#1{}

The following definitions and rules are copied and adjusted from (Tobin-Hochstadt 2010), with the author’s permission. Some of the notations were changed to use those of (Kent et al. 2016).

We include below the grammar, semantics and typing rules related to the minimal core of the Typed Racket language1717 The core language is defined in (Tobin-Hochstadt 2010), pp. 61–70., dubbed λ_{\mathit{TS}}, including extensions which add pairs1818 The extensions needed to handle pairs are described in (Tobin-Hochstadt 2010), pp. 71–75., functions of multiple arguments, variadic functions and variadic polymorphic functions1919 The extensions needed to handle functions of multiple arguments, variadic functions, and variadic functions where the type of the “rest” arguments are not uniform are described in (Tobin-Hochstadt 2010), pp. 91–77., intersection types, recursive types, symbols and promises. These features have been informally described in Overview of Typed Racket’s type system.

We purposefully omit extensions which allow advanced logic reasoning when propagating information gained by complex combinations of conditionals2020 The extensions which allow advanced logic reasoning are described in (Tobin-Hochstadt 2010), pp. 75–78., refinement types2121 The extensions which introduce refinement types are described in (Tobin-Hochstadt 2010), pp. 85–89., dependent refinement types2222 Dependent refinement types are presented in (Kent et al. 2016). (which allow using theories from external solvers to reason about values and their type, e.g. using bitvector theory to ensure that a sequence of operations does not produce a result exceeding a certain machine integer size), structs and classes. These extensions are not relevant to our work2323 We informally describe a translation of our system of records into structs in section [[??]]Todo, but settle for an alternative implementation in section [[??]]Todo which does not rely on structs., and their inclusion in the following semantics would needlessly complicate things.

4.2.1 Notations

We note a sequence of elements with \overrightarrow{y}. When there is more than one sequence involved in a rule or equation, we may use the notation \overrightarrow{y}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{y}} to indicate that there are n elements in the sequence. Two sequences can be forced to have the same number of elements in that way. We represent a set of elements (an “unordered” sequence) with the notation \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{y}. The use of ellipses in α \mathbf{\ldots{}} does not indicate the repetition of α. Instead, it indicates that α is a variadic polymorphic type variable: a placeholder for zero or more types which will be substituted for occurrences of α when the polymorphic type is instantiated. These ellipses appear as such in the Typed Racket source code, and are the reason we use the notation \overrightarrow{y} to indicate repetition, instead of the ellipses commonly used for that purpose. FInally, an empty sequence of repeated elements is sometimes noted ϵ

The judgements are written following the usual convention, where Γ is the environment which associates variables to their type. The Δ environment contains the type variables within scope, and is mostly used to determine the validity of types.

Γ ; Δ ⊢ e : \mathrm{R}

The environments can be extended as follows:

Γ, x : τ ; Δ\cup\{α\} ⊢ e : \mathrm{R}

The typing information \mathrm{R} associated with an expression contains the type of the expression, as well as aliasing information and other propositions which are known to be conditionally true depending on the value of the expression at run-time. These pieces of information are described in more detail below. Since the typing information \mathrm{R} is often inlined in the typing judgement, a typing judgement will generally have the following form:

Γ ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}

In this notation, the + and - signs in \phi{}^+ and \phi{}^- are purely syntactical, and serve to distinguish the positive and negative filters, which are instances of the nonterminal \phi.

The various nonterminals used throughout the language are written in italics and are defined using the notation:

\begin{qaligned} \textit{nonterminal} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \textit{first case}\\ & {}\mathrel{|}{} & \textit{second case}\\ & {}\mathrel{|}{} & \textit{and so on} \end{qaligned}

Additionally, a symbol assigned to a nonterminal may be used as a placeholder in rules and definitions, implicitly indicating that the element used to fill in that placeholder should be an instance of the corresponding nonterminal. When multiple such placeholders are present in a rule, they will be subscripted to distinguish between the different occurrences. The subscripts i, j, k and l are often used for repeated sequences.

In later chapters, we extend already-defined non-terminals using the notation:

\begin{qaligned} \textit{nonterminal} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & \textit{new case}\\ & {}\mathrel{|}{} & \textit{other new case} \end{qaligned}

Typing rules and other rules are described following the usual natural deduction notation.

\frac{\begin{gathered}\textit{hypothesis}\\ \textit{other hypothesis}\end{gathered}}{\begin{gathered}\textit{deduction}\end{gathered}}\ {\rm R{\small U}{\small L}{\small E}\text{-}N{\small A}{\small M}{\small E}}

Metafunctions (i.e. functions which operate on types as syntactical elements, or on other terms of the language) are written in a roman font. The meta-values \mathrm{true} and \mathrm{false} indicate logical truth and falsehood respectively.

\mathrm{metafunction}(x,y) = \begin{cases} \mathrm{true} &\text{ if } x = y + 1\\ \mathrm{false} &\text{ otherwise } \end{cases}

Language operators are written in bold face:

\begin{qaligned} e & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & (\textbf{num}\ n)\\ & {}\mathrel{|}{} & \ldots{} \end{qaligned}

Values are written using a bold italic font:

\begin{qaligned} v & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & (\textbf{$\mathord{{\bfit \text{num}}}$}\ n)\\ & {}\mathrel{|}{} & \ldots{} \end{qaligned}

Type names start with a capital letter, and are written using a bold font:

\begin{qaligned} τ,σ & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & (\textbf{Num}\ n)\\ & {}\mathrel{|}{} & \ldots{} \end{qaligned}

We indicate the syntactical substitution of y with z in w using the notation w[y↦z]. When given several elements to replace, the substitution operator performs a parallel substitution (that is, w[x↦y\ y↦z] will not replace the occurrences of y introduced by the first substitution).

[Succinctly describe the other conventions used in the thesis, if any were omitted above.]Todo

[Define the meta substitution and equality operators precisely.]Todo

4.2.2 Names and bindings

In the following sections, we assume that all type variable names which occur in binding positions are unique. This assumption could be made irrelevant by explicitly renaming in the rules below all type variables to fresh unique ones. Performing this substitution would be a way of encoding a notion of scope and the possibility for one identifier to hide another. However, the Racket language features macros which routinely produce new binding forms. The macro system in Racket is a hygienic one, and relies on a powerful model of the notion of scope (Flatt 2016). Extending the rules below with a simplistic model of Racket’s notion of scope would not do justice to the actual system, and would needlessly complicate the rules. Furthermore, Typed Racket only typechecks fully-expanded programs. In these programs, the binding of each identifier has normally been determined2424 Typed Racket actually still determines the binding for type variables by itself, but we consider this is an implementation detail..

4.2.3 Expressions

The following expressions are available in the subset of Typed Racket which we consider. These expressions include references to variables, creation of basic values (numbers, booleans, lists of pairs ending with \textbf{$\mathord{{\bfit \text{null}}}$}, symbols, promises), a variety of lambda functions with different handling of rest arguments (fixed number of arguments, polymorphic functions with a uniform list of rest arguments and variadic polymorphic functions, as well as polymorphic abstractions), a small sample of primitive functions which are part of Racket’s library and a few operations manipulating these values (function application and polymorphic instantiation, forcing promises, symbol comparison and so on).

\begin{qaligned} e & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & x \ |\ y \ |\ z\hphantom{\text{variable}}\tag*{$\llap{\text{variable}}$}\\ & {}\mathrel{|}{} & (\textbf{num}\ n) \hphantom{\text{number}}\tag*{$\llap{\text{number}}$}\\ & {}\mathrel{|}{} & \textbf{true} \hphantom{\text{booleans}}\tag*{$\llap{\text{booleans}}$}\\ & {}\mathrel{|}{} & \textbf{false}\\ & {}\mathrel{|}{} & \textbf{null} \hphantom{\text{null constant}}\tag*{$\llap{\text{null constant}}$}\\ & {}\mathrel{|}{} & p \hphantom{\text{primitive functions}}\tag*{$\llap{\text{primitive functions}}$}\\ & {}\mathrel{|}{} & \mathbf{(}e\ \overrightarrow{e}\mathbf{)} \hphantom{\text{function application}}\tag*{$\llap{\text{function application}}$}\\ & {}\mathrel{|}{} & (\textbf{if}\ e\ e\ e) \hphantom{\text{conditional}}\tag*{$\llap{\text{conditional}}$}\\ & {}\mathrel{|}{} & \mathbf{λ}(\overrightarrow{x:τ}).e \hphantom{\text{lambda function}}\tag*{$\llap{\text{lambda function}}$}\\ & {}\mathrel{|}{} & \mathbf{λ}(\overrightarrow{x:τ}\ \ .\ \ x:τ*).e \hphantom{\text{variadic function}}\tag*{$\llap{\text{variadic function}}$}\\ & {}\mathrel{|}{} & \mathbf{λ}(\overrightarrow{x:τ}\ \ .\ \ x:τ \mathbf{\ldots{}}_{α}).e \hphantom{\text{variadic polymorpic function}}\tag*{$\llap{\text{variadic polymorpic function}}$}\\ & {}\mathrel{|}{} & \mathbf{\Lambda{}}(\overrightarrow{α}).e\hphantom{\text{polymorphic abstraction}}\tag*{$\llap{\text{polymorphic abstraction}}$}\\ & {}\mathrel{|}{} & \mathbf{\Lambda{}}(\overrightarrow{α}\ α \mathbf{\ldots{}}).e \hphantom{\text{variadic polymorphic abstraction}}\tag*{$\llap{\text{variadic polymorphic abstraction}}$}\\ & {}\mathrel{|}{} & (\textbf{@}\ e\ \overrightarrow{τ}) \hphantom{\text{polymorphic instantiation}}\tag*{$\llap{\text{polymorphic instantiation}}$}\\ & {}\mathrel{|}{} & (\textbf{delay}\ e) \hphantom{\text{create promise}}\tag*{$\llap{\text{create promise}}$}\\ & {}\mathrel{|}{} & (\textbf{force}\ e) \hphantom{\text{force promise}}\tag*{$\llap{\text{force promise}}$}\\ & {}\mathrel{|}{} & (\textbf{symbol}\ s) \hphantom{\text{symbol literal}}\tag*{$\llap{\text{symbol literal}}$}\\ & {}\mathrel{|}{} & (\textbf{gensym}) \hphantom{\text{fresh uninterned symbol}}\tag*{$\llap{\text{fresh uninterned symbol}}$}\\ & {}\mathrel{|}{} & (\textbf{eq?}\ e\ e) \hphantom{\text{symbol equality}}\tag*{$\llap{\text{symbol equality}}$}\\ & {}\mathrel{|}{} & (\textbf{map}\ e\ e) \end{qaligned}

Symbol literals are noted as s \in{} \mathcal{S} and the universe of symbols (which includes symbol literals and fresh symbols created via (\textbf{gensym})) is noted as s{}’ \in{} \mathcal{S}{}’.

\begin{aligned} s & \in{} \mathcal{S}\\ s{}’ & \in{} \mathcal{S}{}’ \\ \mathcal{S} & \subset{} \mathcal{S}{}’ \end{aligned}

4.2.4 Primitive operations (library functions)

Racket offers a large selection of library functions, which we consider as primitive operations. A few of these are listed below, and their type is given later after, once the type system has been introduced. \textit{number?}, \textit{pair?} and \textit{null?} are predicates for the corresponding type. \textit{car} and \textit{cdr} are accessors for the first and second elements of a pair, which can be created using \mathit{cons}. The \textit{identity} function returns its argument unmodified, and \textit{add1} returns its numeric argument plus 1. These last two functions are simply listed as examples.

\begin{qaligned} p & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \textit{add1}\hphantom{\text{returns its argument plus $1$}}\tag*{$\llap{\text{returns its argument plus $1$}}$}\\ & {}\mathrel{|}{} & \textit{number?}\hphantom{\text{number predicate}}\tag*{$\llap{\text{number predicate}}$}\\ & {}\mathrel{|}{} & \textit{pair?}\hphantom{\text{pair predicate}}\tag*{$\llap{\text{pair predicate}}$}\\ & {}\mathrel{|}{} & \textit{null?}\hphantom{\text{$\textbf{$\mathord{{\bfit \text{null}}}$}$ predicate}}\tag*{$\llap{\text{$\textbf{$\mathord{{\bfit \text{null}}}$}$ predicate}}$}\\ & {}\mathrel{|}{} & \textit{identity}\hphantom{\text{identity function}}\tag*{$\llap{\text{identity function}}$}\\ & {}\mathrel{|}{} & \mathit{cons} \hphantom{\text{pair construction}}\tag*{$\llap{\text{pair construction}}$}\\ & {}\mathrel{|}{} & \textit{car}\hphantom{\text{first element of pair}}\tag*{$\llap{\text{first element of pair}}$}\\ & {}\mathrel{|}{} & \textit{cdr}\hphantom{\text{second element of pair}}\tag*{$\llap{\text{second element of pair}}$}\\ & {}\mathrel{|}{} & \ldots{} \end{qaligned}

4.2.5 Values

These expressions and primitive functions may produce or manipulate the following values:

\begin{qaligned} v & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & p \hphantom{\text{primitive function}}\tag*{$\llap{\text{primitive function}}$}\\ & {}\mathrel{|}{} & (\textbf{$\mathord{{\bfit \text{num}}}$}\ n) \hphantom{\text{number}}\tag*{$\llap{\text{number}}$}\\ & {}\mathrel{|}{} & \textbf{$\mathord{{\bfit \text{true}}}$} \hphantom{\text{booleans}}\tag*{$\llap{\text{booleans}}$}\\ & {}\mathrel{|}{} & \textbf{$\mathord{{\bfit \text{false}}}$}\\ & {}\mathrel{|}{} & {\bfit λ}(\overrightarrow{x:τ}).e \hphantom{\text{lambda function}}\tag*{$\llap{\text{lambda function}}$}\\ & {}\mathrel{|}{} & {\bfit λ}(\overrightarrow{x:τ}\ .\ x:τ*).e \hphantom{\text{variadic function}}\tag*{$\llap{\text{variadic function}}$}\\ & {}\mathrel{|}{} & {\bfit λ}(\overrightarrow{x:τ}\ .\ x:τ \mathbf{\ldots{}}_{α}).e \hphantom{\text{variadic polymorphic function}}\tag*{$\llap{\text{variadic polymorphic function}}$}\\ & {}\mathrel{|}{} & {\bfit \Lambda{}}(\overrightarrow{α}).e \hphantom{\text{polymorphic abstraction}}\tag*{$\llap{\text{polymorphic abstraction}}$}\\ & {}\mathrel{|}{} & {\bfit \Lambda{}}(\overrightarrow{α}\ α \mathbf{\ldots{}}).e \hphantom{\text{variadic polymorphic abstraction}}\tag*{$\llap{\text{variadic polymorphic abstraction}}$}\\ & {}\mathrel{|}{} & \langle{}v, v\rangle{} \hphantom{\text{pair}}\tag*{$\llap{\text{pair}}$}\\ & {}\mathrel{|}{} & \textbf{$\mathord{{\bfit \text{null}}}$} \hphantom{\text{null}}\tag*{$\llap{\text{null}}$}\\ & {}\mathrel{|}{} & (\textbf{$\mathord{{\bfit \text{promise}}}$}\ e) \hphantom{\text{promise}}\tag*{$\llap{\text{promise}}$}\\ & {}\mathrel{|}{} & (\textbf{$\mathord{{\bfit \text{symbol}}}$}\ s{}’) \hphantom{\text{symbol}}\tag*{$\llap{\text{symbol}}$} \end{qaligned}

The \textbf{$\mathord{{\bfit \text{list}}}$} value notation is defined as a shorthand for a \textbf{$\mathord{{\bfit \text{null}}}$}-terminated linked list of pairs.

\begin{aligned} (\textbf{$\mathord{{\bfit \text{list}}}$}\ v{}_0\ \overrightarrow{v{}_i}) &\stackrel{\scriptscriptstyle\mathsf{def}}{=} \langle{}v{}_0, (\textbf{$\mathord{{\bfit \text{list}}}$}\ \overrightarrow{v{}_i})\rangle{} \\ (\textbf{$\mathord{{\bfit \text{list}}}$}) &\stackrel{\scriptscriptstyle\mathsf{def}}{=} \textbf{$\mathord{{\bfit \text{null}}}$} \\ \end{aligned}

4.2.6 Evaluation contexts

The operational semantics given below rely on the following evaluation contexts:

\begin{qaligned} E & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & [\cdot{}] \hphantom{\text{program entry point}}\tag*{$\llap{\text{program entry point}}$}\\ & {}\mathrel{|}{} & \mathbf{(}\overrightarrow{v}\ E\ \overrightarrow{e}\mathbf{)}\hphantom{\text{function application}}\tag*{$\llap{\text{function application}}$}\\ & {}\mathrel{|}{} & (\textbf{if}\ E\ e\ e)\hphantom{\text{conditional}}\tag*{$\llap{\text{conditional}}$}\\ & {}\mathrel{|}{} & (\textbf{eq?}\ E\ e)\hphantom{\text{symbol equality}}\tag*{$\llap{\text{symbol equality}}$}\\ & {}\mathrel{|}{} & (\textbf{eq?}\ v\ E)\\ & {}\mathrel{|}{} & (\textbf{map}\ E\ e)\hphantom{\text{map function over list}}\tag*{$\llap{\text{map function over list}}$}\\ & {}\mathrel{|}{} & (\textbf{map}\ v\ E) \end{qaligned}

4.2.7 Typing judgement

Γ ; Δ ⊢ e : \mathrm{R}

\begin{qaligned} \mathrm{R} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \end{qaligned}

The Γ ; Δ ⊢ e : \mathrm{R} typing judgement indicates that the expression e has type τ. The Γ typing environment maps variables to their type (and to extra information), while the Δ environment stores the polymorphic type variables, variadic polymorphic type variables and recursive type variables which are in scope.

Additionally, the typing judgement indicates a set of propositions \phi{}^- which are known to be true when the run-time value of e is \textbf{$\mathord{{\bfit \text{false}}}$}, and a set of propositions \phi{}^+ which are known to be true when the run-time value of e is \textbf{$\mathord{{\bfit \text{true}}}$}2525 Any other value is treated in the same way as \textbf{$\mathord{{\bfit \text{true}}}$}, as values other than \textbf{$\mathord{{\bfit \text{false}}}$} are traditionally considered as true in language of the Lisp family.. The propositions will indicate that the value of a separate variable belongs (or does not belong) to a given type. For example, the \phi{}^- proposition \mathbf{Number}_y indicates that when e evaluates to \textbf{$\mathord{{\bfit \text{false}}}$}, the variable y necessarily holds an integer.

Finally, the typing judgement can indicate with o that the expression e is an alias for a sub-element of another variable in the environment. For example, if the object o is \mathrm{car} :: \mathrm{cdr}(y), it indicates that the expression e produces the same value that (car (cdr y)) would, i.e. that it returns the second element of a (possibly improper) list stored in y.

Readers familiar with abstract interpretation can compare the \phi propositions to the Cartesian product of the abstract domains of pairs of variables. A static analyser can track possible pairs of values contained in pairs of distinct variables, and will represent this information using an abstract domain which combinations of values may be possible, and which may not. Occurrence typing similarly exploits the fact that the type of other variables may depend on the value of τ.

4.2.8 Types

Typed Racket handles the types listed below. Aside from the top type (⊤) which is the supertype of all other types, this list includes singleton types for numbers, booleans, symbols and the \textbf{$\mathord{{\bfit \text{null}}}$} value. The types \mathbf{Number} and \mathbf{Symbol} are the infinite unions of all number and symbol singletons, respectively. Also present are function types (with fixed arguments, homogeneous rest arguments and the variadic polymorphic functions which accept heterogeneous rest arguments, as well as polymorphic abstractions), unions of other types, intersections of other types, the type of pairs and promises. The value assigned to a variadic polymorphic function’s rest argument will have a type of the form (\textbf{List}\ τ \mathbf{\ldots{}}_{α}). Finally, Typed Racket allows recursive types to be described with the \textbf{Rec} combinator.

\begin{qaligned} τ,σ & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & ⊤\hphantom{\text{top}}\tag*{$\llap{\text{top}}$}\\ & {}\mathrel{|}{} & (\textbf{Num}\ n) \hphantom{\text{number singleton}}\tag*{$\llap{\text{number singleton}}$}\\ & {}\mathrel{|}{} & \mathbf{Number} \hphantom{\text{any number}}\tag*{$\llap{\text{any number}}$}\\ & {}\mathrel{|}{} & \textbf{True} \hphantom{\text{boolean singleton}}\tag*{$\llap{\text{boolean singleton}}$}\\ & {}\mathrel{|}{} & \textbf{False}\\ & {}\mathrel{|}{} & (\textbf{Symbol}\ s{}’) \hphantom{\text{symbol singleton}}\tag*{$\llap{\text{symbol singleton}}$}\\ & {}\mathrel{|}{} & \mathbf{Symbol} \hphantom{\text{any symbol}}\tag*{$\llap{\text{any symbol}}$}\\ & {}\mathrel{|}{} & (\overrightarrow{τ}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \hphantom{\text{function}}\tag*{$\llap{\text{function}}$}\\ & {}\mathrel{|}{} & (\overrightarrow{τ}\ \ {\mathbf{.}}\ \ τ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \hphantom{\text{variadic function}}\tag*{$\llap{\text{variadic function}}$}\\ & {}\mathrel{|}{} & (\overrightarrow{τ}\ \ {\mathbf{.}}\ \ τ \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \hphantom{\text{variadic polymorphic function}}\tag*{$\llap{\text{variadic polymorphic function}}$}\\ & {}\mathrel{|}{} & (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α})\ τ)\hphantom{\text{polymorphic type}}\tag*{$\llap{\text{polymorphic type}}$}\\ & {}\mathrel{|}{} & (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α}\ α \mathbf{\ldots{}})\ τ) \hphantom{\text{variadic polymorphic type}}\tag*{$\llap{\text{variadic polymorphic type}}$}\\ & {}\mathrel{|}{} & α \ |\ β\hphantom{\text{polymorphic type variable}}\tag*{$\llap{\text{polymorphic type variable}}$}\\ & {}\mathrel{|}{} & (\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ})\hphantom{\text{union}}\tag*{$\llap{\text{union}}$}\\ & {}\mathrel{|}{} & (\textbf{$\cap$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ}) \hphantom{\text{intersection}}\tag*{$\llap{\text{intersection}}$}\\ & {}\mathrel{|}{} & \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\hphantom{\text{pair}}\tag*{$\llap{\text{pair}}$}\\ & {}\mathrel{|}{} & \textbf{Null} \hphantom{\text{null (end of lists)}}\tag*{$\llap{\text{null (end of lists)}}$}\\ & {}\mathrel{|}{} & (\textbf{List}\ τ \mathbf{\ldots{}}_{α}) \hphantom{\text{variadic polymorphic list}}\tag*{$\llap{\text{variadic polymorphic list}}$}\\ & {}\mathrel{|}{} & (\textbf{Promise}\ \mathrm{R}) \hphantom{\text{promise}}\tag*{$\llap{\text{promise}}$}\\ & {}\mathrel{|}{} & (\textbf{Rec}\ r\ τ) \hphantom{\text{recursive type}}\tag*{$\llap{\text{recursive type}}$} \end{qaligned}

Additionally, the \mathbf{Boolean} type is defined as the union of the \textbf{True} and \textbf{False} singleton types, and the \textbf{List} type operator is a shorthand for describing the type of \textbf{$\mathord{{\bfit \text{null}}}$}-terminated heterogeneous linked lists of pairs, with a fixed length. The \textbf{Listof} type operator is a shorthand for describing the type of \textbf{$\mathord{{\bfit \text{null}}}$}-terminated homogeneous linked lists of pairs, with an unspecified length.

\mathbf{Boolean} \mathrel{\stackrel{\scriptscriptstyle\mathsf{def}}{=}} (\textbf{$\cup$}\ \textbf{True}\ \textbf{False})

\begin{aligned} (\textbf{List}\ τ\ \overrightarrow{σ}) \mathrel{\stackrel{\scriptscriptstyle\mathsf{def}}{=}} \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} (\textbf{List}\ \overrightarrow{σ})\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭} \\ (\textbf{List}) \mathrel{\stackrel{\scriptscriptstyle\mathsf{def}}{=}} \textbf{Null} \end{aligned}

(\textbf{Listof}\ τ) \mathrel{\stackrel{\scriptscriptstyle\mathsf{def}}{=}} (\textbf{Rec}\ r\ (\textbf{$\cup$}\ \textbf{Null}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} r\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}))

4.2.9 Filters (value-dependent propositions)

The filters associated with an expression are a set of positive (resp. negative) propositions which are valid when the expression is true (resp. false).

\begin{qaligned} \phi & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ}\hphantom{\text{filter set}}\tag*{$\llap{\text{filter set}}$} \end{qaligned}

These propositions indicate that a specific subelement of a location has a given type.

\begin{qaligned} ψ & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & τ_{π(\mathit{loc})} \hphantom{\text{$(v = \mathbf{?}) \Rightarrow{} π(\mathit{loc})\text{ is of type $τ$}$}}\tag*{$\llap{\text{$(v = \mathbf{?}) \Rightarrow{} π(\mathit{loc})\text{ is of type $τ$}$}}$}\\ & {}\mathrel{|}{} & \overline{τ}_{π(\mathit{loc})} \hphantom{\text{$(v = \mathbf{?}) \Rightarrow{} π(\mathit{loc})\text{ is not of type $τ$}$}}\tag*{$\llap{\text{$(v = \mathbf{?}) \Rightarrow{} π(\mathit{loc})\text{ is not of type $τ$}$}}$}\\ & {}\mathrel{|}{} & ⊥\hphantom{\text{contradiction}}\tag*{$\llap{\text{contradiction}}$} \end{qaligned}

The location can be a variable, or the special \bullet{} token, which denotes a function’s first parameter, when the propositions are associated with that function’s result. This allows us to express relations between the output of a function and its input, without referring to the actual name of the parameter, which is irrelevant. In other words, \bullet{} occurs in an α-normal form of a function’s type.

\begin{qaligned} \mathit{loc} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \bullet{}\hphantom{\text{first argument of the function}}\tag*{$\llap{\text{first argument of the function}}$}\\ & {}\mathrel{|}{} & x\hphantom{\text{variable}}\tag*{$\llap{\text{variable}}$} \end{qaligned}

Objects, which represent aliasing information, can either indicate that the expression being considered is an alias for a sub-element of a variable, or that no aliasing information is known.

4.2.10 Objects (aliasing information)

\begin{qaligned} \textrm{o} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & π(\mathit{loc})\hphantom{\text{$e$ is an alias for $π(\mathit{loc})$}}\tag*{$\llap{\text{$e$ is an alias for $π(\mathit{loc})$}}$}\\ & {}\mathrel{|}{} & \emptyset{}\hphantom{\text{no aliasing information}}\tag*{$\llap{\text{no aliasing information}}$} \end{qaligned}

Sub-elements are described via a chain of path elements which are used to access the sub-element starting from the variable.

4.2.11 Paths

\begin{qaligned} \textit{π} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & pe::π\hphantom{\text{path concatenation}}\tag*{$\llap{\text{path concatenation}}$}\\ & {}\mathrel{|}{} & ϵ \hphantom{\text{empty path}}\tag*{$\llap{\text{empty path}}$} \end{qaligned}

The path concatenation operator :: is associative. . The ϵ is omitted from paths with one or more elements, so we write car::cdr instead of car::cdr::ϵ.

4.2.12 Path elements

Path elements can be \mathrm{car} and \mathrm{cdr}, to indicate access to a pair’s first or second element, and \mathrm{force}, to indicate that the proposition or object targets the result obtained after forcing a promise. We will note here that this obviously is only sound if forcing a promise always returns the same result (otherwise the properties and object which held on a former value may hold on the new result). Racket features promises which do not cache their result. These could return a different result each time they are forced by relying on external state. However, forcing a promise is generally assumed to be an idempotent operation, and not respecting this implicit contract in production code would be bad practice. Typed Racket disallows non-cached promises altogether. We introduced a small module delay-pure which allows the safe creation of non-cached promises. delay-pure restricts the language to a small subset of functions and operators which are known to not perform any mutation, and prevents access to mutable variables. This ensures that the promises created that way always produce the same value, without the need to actually cache their result.

\begin{qaligned} \textit{pe} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \mathrm{car} \hphantom{\text{first element of pair}}\tag*{$\llap{\text{first element of pair}}$}\\ & {}\mathrel{|}{} & \mathrm{cdr} \hphantom{\text{second element of pair}}\tag*{$\llap{\text{second element of pair}}$}\\ & {}\mathrel{|}{} & \mathrm{force} \hphantom{\text{result of a promise}}\tag*{$\llap{\text{result of a promise}}$} \end{qaligned}

4.2.13 Subtyping

The subtyping judgement is ⊢ τ \mathrel{≤:} σ. It indicates that τ is a subtype of σ (or that τ and σ are the same type).

The {\mathrel{≤:}} relation is reflexive and transitive. When two or more types are all subtypes of each other, they form an equivalence class. They are considered different notations for the same type, and we note ⊢ τ \mathrel{=:} σ, whereas ⊢ τ \mathrel{\neq:} σ indicates that τ and σ are not mutually subtypes of each other (but one can be a strict subtype of the other).

\frac{\begin{gathered}⊢ τ \mathrel{=:} σ\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} σ\end{gathered}}\ {\rm S\text{-}E{\small Q}}_1

\frac{\begin{gathered}⊢ τ \mathrel{=:} σ\end{gathered}}{\begin{gathered}⊢ σ \mathrel{≤:} τ\end{gathered}}\ {\rm S\text{-}E{\small Q}}_2

\frac{\begin{gathered}⊢ τ \mathrel{≤:} σ \\ ⊢ σ \mathrel{≤:} τ\end{gathered}}{\begin{gathered}⊢ τ \mathrel{=:} σ\end{gathered}}\ {\rm S\text{-}E{\small Q}}_3

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} τ\end{gathered}}\ {\rm S\text{-}R{\small E}{\small F}{\small L}{\small E}{\small X}{\small I}{\small V}{\small E}}

\frac{\begin{gathered}⊢ τ \mathrel{≤:} τ{}’ \\ ⊢ τ{}’ \mathrel{≤:} τ{}”\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} τ{}”\end{gathered}}\ {\rm S\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}}

The ⊥ type is a shorthand for the empty union (\cup). It is a subtype of every other type, and is not inhabited by any value. {\rm S\text{-}B{\small O}{\small T}\text{-}S{\small U}{\small B}} can be derived from {\rm S\text{-}B{\small O}{\small T}} and {\rm S\text{-}U{\small N}{\small I}{\small O}{\small N}S{\small U}{\small B}}, by constructing an empty union.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} ⊤\end{gathered}}\ {\rm S\text{-}T{\small O}{\small P}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ ⊥ \mathrel{=:} (\textbf{$\cup$})\end{gathered}}\ {\rm S\text{-}B{\small O}{\small T}}

\begin{array}[b]{c} \begin{array}[b]{c} \begin{array}[b]{c} {\rm S\text{-}B{\small O}{\small T}} \\\hline {\rm S\text{-}E{\small Q}{\small {}_1}} \end{array} \quad{}{\rm S\text{-}U{\small N}{\small I}{\small O}{\small N}S{\small U}{\small B}} \\\hline {\rm S\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}} \end{array} \\\hline ⊢ ⊥ \mathrel{≤:} τ \end{array} \ \smash{ \begin{array}[c]{c} {\rm S\text{-}B{\small O}{\small T}\text{-}S{\small U}{\small B}} \\[1ex] \vphantom{⊢ ⊥ \mathrel{≤:} τ} \end{array}}

The singleton types (\textbf{Num}\ n) and (\textbf{Symbol}\ s) which are only inhabited by their literal counterpart are subtypes of the more general \mathbf{Number} or \mathbf{Symbol} types, respectively.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ (\textbf{Num}\ n) \mathrel{≤:} \mathbf{Number}\end{gathered}}\ {\rm S\text{-}N{\small U}{\small M}{\small B}{\small E}{\small R}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ (\textbf{Symbol}\ s) \mathrel{≤:} \mathbf{Symbol}\end{gathered}}\ {\rm S\text{-}S{\small Y}{\small M}{\small B}{\small O}{\small L}}

The following subtyping rules are concerned with function types and polymorphic types:

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\overrightarrow{τ_a}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \mathrel{≤:} (\overrightarrow{σ_a}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}F{\small U}{\small N}}

\frac{\begin{gathered}⊢ τ_r \mathrel{≤:} σ_r \\ \phi{}^+{}’ \subseteq{} \phi{}^+ \\ \phi{}^-{}’ \subseteq{} \phi{}^- \\ o = o{}’ ∨ o{}’ = \emptyset{}\end{gathered}}{\begin{gathered}⊢ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_r \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \mathrel{{≤:}_R} {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}σ_r \;{\mathbf{;}}\; \phi{}^+{}’ {\mathbf{{/}}} \phi{}^-{}’ \;{\mathbf{;}}\; o{}’{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm S\text{-}R}

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ ⊢ σ \mathrel{≤:} τ \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\overrightarrow{τ_a}\ \ {\mathbf{.}}\ \ τ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \mathrel{≤:} (\overrightarrow{σ_a}\ \ {\mathbf{.}}\ \ σ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}F{\small U}{\small N}{\small *}}

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ \overrightarrow{⊢ σ{}_i \mathrel{≤:} τ} \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\overrightarrow{τ_a}\ \ {\mathbf{.}}\ \ τ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \mathrel{≤:} (\overrightarrow{σ_a}\ \overrightarrow{σ{}_i}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}F{\small U}{\small N}{\small *}\text{-}F{\small I}{\small X}{\small E}{\small D}}

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ \overrightarrow{⊢ σ{}_i \mathrel{≤:} τ} \\ ⊢ σ \mathrel{≤:} τ \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\overrightarrow{τ_a}\ \ {\mathbf{.}}\ \ τ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \mathrel{≤:} (\overrightarrow{σ_a}\ \overrightarrow{σ{}_i}\ \ {\mathbf{.}}\ \ σ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}F{\small U}{\small N}{\small *}\text{-}F{\small I}{\small X}{\small E}{\small D}{\small *}}

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ ⊢ σ \mathrel{≤:} τ \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\overrightarrow{τ_a}\ \ {\mathbf{.}}\ \ τ \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}) \mathrel{≤:} (\overrightarrow{σ_a}\ \ {\mathbf{.}}\ \ σ \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}DF{\small U}{\small N}}

\frac{\begin{gathered}⊢ τ[\overrightarrow{α{}_i ↦ β{}_i}] \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_i})\ τ) \mathrel{≤:} (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{β{}_i})\ σ)\end{gathered}}\ {\rm S\text{-}P{\small O}{\small L}{\small Y}\text{-}}α{\rm \text{-}E{\small Q}{\small U}{\small I}{\small V}}

\frac{\begin{gathered}⊢ τ[\overrightarrow{α{}_i ↦ β{}_i} α ↦ β] \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_i}\ α \mathbf{\ldots{}})\ τ) \mathrel{≤:} (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{β{}_i}\ β \mathbf{\ldots{}})\ σ)\end{gathered}}\ {\rm S\text{-}P{\small O}{\small L}{\small Y}D\text{-}}α{\rm \text{-}E{\small Q}{\small U}{\small I}{\small V}}

\frac{\begin{gathered}\overrightarrow{⊢ σ_a \mathrel{≤:} τ_a} \\ ⊢ σ \mathrel{≤:} τ[α ↦ ⊤] \\ ⊢ \mathrm{R} \mathrel{{≤:}_R} \mathrm{R}{}’\end{gathered}}{\begin{gathered}⊢ (\textbf{${\mathbf{\forall{}}}$}\ (α \mathbf{\ldots{}})\ (\overrightarrow{τ_a}\ \ {\mathbf{.}}\ \ τ \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \mathrm{R})) \mathrel{≤:} (\overrightarrow{σ_a}\ \ {\mathbf{.}}\ \ σ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R}{}’)\end{gathered}}\ {\rm S\text{-}DF{\small U}{\small N}\text{-}F{\small U}{\small N}{\small *}}

[{\rm S\text{-}P{\small O}{\small L}{\small Y}D\text{-}{\small Α}\text{-}E{\small Q}{\small U}{\small I}{\small V}} should use the substitution for a polydot (subst-dots?), not the usual subst.]Todo

[check the {\rm S\text{-}DF{\small U}{\small N}\text{-}F{\small U}{\small N}{\small *}} rule.]Todo

The following rules are concerned with recursive types built with the Rec combinator. The {\rm S\text{-}R{\small E}{\small C}W{\small R}{\small A}{\small P}} rule allows considering \mathbf{Number} a subtype of (\textbf{Rec}\ r\ \mathbf{Number}) for example (i.e. applying the recursive type combinator to a type which does not refer to r is a no-op), but it also allows deriving ⊢ (\textbf{Rec}\ r\ (\textbf{$\cup$}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} r\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ \textbf{Null})) \mathrel{≤:} (\textbf{$\cup$}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} ⊤\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ \textbf{Null}). The {\rm {\small }S\text{-}R{\small E}{\small C}E{\small L}{\small I}{\small M}} rule has the opposite effect, and is mainly useful to “upcast” members of an union containing r. It allows the deriving ⊢ \textbf{Null} \mathrel{≤:} (\textbf{Rec}\ r\ (\textbf{$\cup$}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} r\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ \textbf{Null})). The rules {\rm {\small }S\text{-}R{\small E}{\small C}S{\small T}{\small E}{\small P}} and {\rm S\text{-}R{\small E}{\small C}U{\small N}S{\small T}{\small E}{\small P}} allow unraveling a single step of the recursion, or assimilating an such an unraveled step as part of the recursive type.

[TODO: renamings]Todo

\frac{\begin{gathered}⊢ τ \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{Rec}\ r\ τ) \mathrel{≤:} σ\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}W{\small R}{\small A}{\small P}}

\frac{\begin{gathered}⊢ τ \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} (\textbf{Rec}\ r\ σ)\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}E{\small L}{\small I}{\small M}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ σ[r↦(\textbf{Rec}\ r\ σ)] \mathrel{≤:} (\textbf{Rec}\ r\ σ)\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}S{\small T}{\small E}{\small P}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ (\textbf{Rec}\ r\ σ) \mathrel{≤:} σ[r↦(\textbf{Rec}\ r\ σ)]\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}U{\small N}S{\small T}{\small E}{\small P}}

The rules below describe how union and intersection types compare.

\frac{\begin{gathered}\exists{} i . ⊢ τ \mathrel{≤:} σ{}_i\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} (\textbf{$\cup$}\ \overrightarrow{σ{}_i})\end{gathered}}\ {\rm S\text{-}U{\small N}{\small I}{\small O}{\small N}S{\small U}{\small P}{\small E}{\small R}}

\frac{\begin{gathered}\overrightarrow{⊢ τ{}_i \mathrel{≤:} σ}\end{gathered}}{\begin{gathered}⊢ (\textbf{$\cup$}\ \overrightarrow{τ{}_i}) \mathrel{≤:} σ\end{gathered}}\ {\rm S\text{-}U{\small N}{\small I}{\small O}{\small N}S{\small U}{\small B}}

\frac{\begin{gathered}\exists{} i . ⊢ σ{}_i \mathrel{≤:} τ\end{gathered}}{\begin{gathered}⊢ \bigcap{} \overrightarrow{σ{}_i} \mathrel{≤:} τ\end{gathered}}\ {\rm S\text{-}I{\small N}{\small T}{\small E}{\small R}{\small S}{\small E}{\small C}{\small T}{\small I}{\small O}{\small N}S{\small U}{\small B}}

\frac{\begin{gathered}\overrightarrow{⊢ σ \mathrel{≤:} τ{}_i}\end{gathered}}{\begin{gathered}⊢ σ \mathrel{≤:} \bigcap{} \overrightarrow{τ{}_i}\end{gathered}}\ {\rm S\text{-}I{\small N}{\small T}{\small E}{\small R}{\small S}{\small E}{\small C}{\small T}{\small I}{\small O}{\small N}S{\small U}{\small P}{\small E}{\small R}}

Finally, promises are handled by comparing the type that they produce when forced, and pairs are compared pointwise. Dotted lists types, which usually represent the type of the value assigned to a variadic polymorphic function’s “rest” argument

\frac{\begin{gathered}⊢ τ \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{Promise}\ τ) \mathrel{≤:} (\textbf{Promise}\ σ)\end{gathered}}\ {\rm S\text{-}P{\small R}{\small O}{\small M}{\small I}{\small S}{\small E}}

\frac{\begin{gathered}⊢ τ{}_1 \mathrel{≤:} σ{}_1 \\ ⊢ τ{}_2 \mathrel{≤:} σ{}_2\end{gathered}}{\begin{gathered}⊢ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{}_1{\mathbf{,}} τ{}_2\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭} \mathrel{≤:} \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}σ{}_1{\mathbf{,}} σ{}_2\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\end{gathered}}\ {\rm S\text{-}P{\small A}{\small I}{\small R}}

\frac{\begin{gathered}⊢ τ \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{List}\ τ \mathbf{\ldots{}}_{α}) \mathrel{≤:} (\textbf{Rec}\ r\ (\textbf{$\cup$}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}σ{\mathbf{,}} r\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ \textbf{Null}))\end{gathered}}\ {\rm S\text{-}DL{\small I}{\small S}{\small T}}

4.2.14 Operational semantics

The semantics for the simplest expressions and for primitive functions are expressed using δ-rules.

\frac{\begin{gathered}δ(p,\overrightarrow{v}) = v{}’\end{gathered}}{\begin{gathered}\mathbf{(}p\ \overrightarrow{v}\mathbf{)} ↪ v{}’\end{gathered}}\ {\rm E\text{-}D{\small E}{\small L}{\small T}{\small A}}

\frac{\begin{gathered}δ_{\mathrm{e}}(e) = v\end{gathered}}{\begin{gathered}e ↪ v{}’\end{gathered}}\ {\rm E\text{-}D{\small E}{\small L}{\small T}{\small A}E}

\begin{aligned} δ(\textit{add1}, (\textbf{$\mathord{{\bfit \text{num}}}$}\ n)) &= (\textbf{$\mathord{{\bfit \text{num}}}$}\ n+1) & \\ δ(\textit{number?}, (\textbf{$\mathord{{\bfit \text{num}}}$}\ n)) &= \textbf{$\mathord{{\bfit \text{true}}}$} & \\ δ(\textit{number?}, v) &= \textbf{$\mathord{{\bfit \text{false}}}$} & \text{otherwise} \\ δ(\mathit{cons}, v{}_1, v{}_2) &= \langle{}v{}_1, v{}_2\rangle{} & \\ δ(\textit{car}, \langle{}v{}_1, v{}_2\rangle{}) &= v{}_1 & \\ δ(\textit{cdr}, \langle{}v{}_1, v{}_2\rangle{}) &= v{}_2 & \\ δ(\textit{pair?}, \langle{}v, v\rangle{}) &= \textbf{$\mathord{{\bfit \text{true}}}$} & \\ δ(\textit{pair?}, v) &= \textbf{$\mathord{{\bfit \text{false}}}$} & \text{otherwise} \\ δ(\textit{null?}, \textbf{$\mathord{{\bfit \text{null}}}$}) &= \textbf{$\mathord{{\bfit \text{true}}}$} & \\ δ(\textit{null?}, v) &= \textbf{$\mathord{{\bfit \text{false}}}$} & \text{otherwise} \\ δ(\textit{identity}, v) &= v & \\ \end{aligned}

\begin{aligned} δ_{\mathrm{e}}((\textbf{num}\ n)) = (\textbf{$\mathord{{\bfit \text{num}}}$}\ n) \\ δ_{\mathrm{e}}(\textbf{true}) = \textbf{$\mathord{{\bfit \text{true}}}$} \\ δ_{\mathrm{e}}(\textbf{false}) = \textbf{$\mathord{{\bfit \text{false}}}$} \\ δ_{\mathrm{e}}(\textbf{null}) = \textbf{$\mathord{{\bfit \text{null}}}$} \\ δ_{\mathrm{e}}(\mathbf{λ}(\overrightarrow{x:τ}).e) = {\bfit λ}(\overrightarrow{x_r:τ}).e \\ δ_{\mathrm{e}}(\mathbf{λ}(\overrightarrow{x:τ}\ \ .\ \ x_r:σ*).e) = {\bfit λ}(\overrightarrow{x:τ}\ .\ x:σ*).e \\ δ_{\mathrm{e}}(\mathbf{λ}(\overrightarrow{x:τ}\ \ .\ \ x_r:σ \mathbf{\ldots{}}_{α}).e) = {\bfit λ}(\overrightarrow{x:τ}\ .\ x_r:σ \mathbf{\ldots{}}_{α}).e \\ δ_{\mathrm{e}}(\mathbf{\Lambda{}}(\overrightarrow{α}).e) = {\bfit \Lambda{}}(\overrightarrow{α}).e \\ δ_{\mathrm{e}}(\mathbf{\Lambda{}}(\overrightarrow{α}\ β \mathbf{\ldots{}}).e) = {\bfit \Lambda{}}(\overrightarrow{α}\ β \mathbf{\ldots{}}).e \\ δ_{\mathrm{e}}((\textbf{delay}\ e)) = (\textbf{$\mathord{{\bfit \text{promise}}}$}\ e) \\ δ_{\mathrm{e}}((\textbf{symbol}\ s)) = (\textbf{$\mathord{{\bfit \text{symbol}}}$}\ s) \end{aligned}

The {\rm E\text{-}C{\small O}{\small N}{\small T}{\small E}{\small X}{\small T}} rule indicates that when the expression has the shape E[L], the subpart L can be evaluated and replaced by its result. The syntax E[L] indicates the replacement of the only occurrence of [\cdot{}] within an evaluation context E. The evaluation context can then match an expression with the same shape, thereby separating the L part from its context.

\frac{\begin{gathered}L ↪ R\end{gathered}}{\begin{gathered}E[L] ↪ E[R]\end{gathered}}\ {\rm E\text{-}C{\small O}{\small N}{\small T}{\small E}{\small X}{\small T}}

The next rules handle β-reduction for the various flavours of functions.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}\mathbf{(}{\bfit λ}(\overrightarrow{x:τ}).e_b\ \overrightarrow{e_a}\mathbf{)} ↪ e_b[\overrightarrow{x ↦ e_a}]\end{gathered}}\ {\rm E\text{-}B{\small E}{\small T}{\small A}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}\mathbf{(}{\bfit λ}(\overrightarrow{x:τ}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{x:τ}}\ .\ x_r:τ_r*).e_b\ \overrightarrow{e_a}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{e_a}}\ \overrightarrow{e_r}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{e_r}}\mathbf{)} ↪ e_b[x_r↦(\textbf{$\mathord{{\bfit \text{list}}}$}\ \overrightarrow{e_r}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{e_r}})\ \overrightarrow{x ↦ e_a}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{x ↦ e_a}}]\end{gathered}}\ {\rm E\text{-}B{\small E}{\small T}{\small A}{\small *}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}\mathbf{(}{\bfit λ}(\overrightarrow{x:τ}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{x:τ}}\ .\ x_r:τ_r \mathbf{\ldots{}}_{α}).e_b\ \overrightarrow{e_a}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{e_a}}\ \overrightarrow{e_r}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{e_r}}\mathbf{)} ↪ e_b[x_r↦(\textbf{$\mathord{{\bfit \text{list}}}$}\ \overrightarrow{e_r}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{e_r}})\ \overrightarrow{x ↦ e_a}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{x ↦ e_a}}]\end{gathered}}\ {\rm E\text{-}B{\small E}{\small T}{\small A}D}

Instantiation of polymorphic abstractions is a no-op at run-time, because Typed Racket performs type erasure (no typing information subsists at run-time, aside from the implicit tags used to distinguish the various primitive data types: pairs, numbers, symbols, \textbf{$\mathord{{\bfit \text{null}}}$}, \textbf{$\mathord{{\bfit \text{true}}}$}, \textbf{$\mathord{{\bfit \text{false}}}$}, functions and promises).

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{@}\ {\bfit \Lambda{}}(\overrightarrow{α}).e\ \overrightarrow{τ}) ↪ e\end{gathered}}\ {\rm E\text{-}TB{\small E}{\small T}{\small A}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{@}\ {\bfit \Lambda{}}(\overrightarrow{α}\ β \mathbf{\ldots{}}).e\ \overrightarrow{τ}) ↪ e\end{gathered}}\ {\rm E\text{-}TDB{\small E}{\small T}{\small A}}

\mathbf{λ}(\overrightarrow{x:τ}\ \ .\ \ x:τ*).e

For simplicity, we assume that promises only contain pure expressions, and therefore that the expression always produces the same value (modulo object identity, i.e. pointer equality issues). In practice, Typed Racket allows expressions relying on external state, and caches the value obtained after forcing the promise for the first time. The subset of the language which we present here does not contain any mutable value, and does not allow mutation of variables either, so the expression wrapped by promises is, by definition, pure. We note here that we implemented a small library for Typed Racket which allows the creation of promises encapsulating a pure expression, and whose result is not cached.

\frac{\begin{gathered}e ↪ v\end{gathered}}{\begin{gathered}(\textbf{force}\ (\textbf{$\mathord{{\bfit \text{promise}}}$}\ e)) ↪ v\end{gathered}}\ {\rm E\text{-}F{\small O}{\small R}{\small C}{\small E}}

Once the evaluation context rule has been applied to evaluate the condition of an \textbf{if} expression, the evaluation continues with the then branch or with the else branch, depending on the condition’s value. Following Lisp tradition, all values other than \textbf{$\mathord{{\bfit \text{false}}}$} are interpreted as a true condition.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{if}\ \textbf{$\mathord{{\bfit \text{false}}}$}\ e{}_2\ e{}_3) ↪ e{}_3\end{gathered}}\ {\rm E\text{-}I{\small F}\text{-}F{\small A}{\small L}{\small S}{\small E}}

\frac{\begin{gathered}v \neq \textbf{$\mathord{{\bfit \text{false}}}$}\end{gathered}}{\begin{gathered}(\textbf{if}\ v\ e{}_2\ e{}_3) ↪ e{}_3\end{gathered}}\ {\rm E\text{-}I{\small F}\text{-}T{\small R}{\small U}{\small E}}

The \textbf{gensym} expression produces a fresh symbol s{}’ \in{} \mathcal{S}*, which is guaranteed to be different from all symbol literals s \in{} \mathcal{S}, and different from all previous and future symbols returned by \textbf{gensym}. The \textbf{eq?} operator can then be used to compare symbol literals and symbols produced by \textbf{gensym}.

\frac{\begin{gathered}v = s{}’ \text{ fresh}\end{gathered}}{\begin{gathered}(\textbf{gensym}) ↪ v\end{gathered}}\ {\rm E\text{-}G{\small E}{\small N}{\small S}{\small Y}{\small M}}

\frac{\begin{gathered}v{}_1 = v{}_2\end{gathered}}{\begin{gathered}(\textbf{eq?}\ v{}_1\ v{}_2) ↪ \textbf{$\mathord{{\bfit \text{true}}}$}\end{gathered}}\ {\rm E\text{-}E{\small Q}{\small ?}\text{-}T{\small R}{\small U}{\small E}}

\frac{\begin{gathered}v{}_1 \neq v{}_2\end{gathered}}{\begin{gathered}(\textbf{eq?}\ v{}_1\ v{}_2) ↪ \textbf{$\mathord{{\bfit \text{false}}}$}\end{gathered}}\ {\rm E\text{-}E{\small Q}{\small ?}\text{-}F{\small A}{\small L}{\small S}{\small E}}

The semantics of \textbf{map} are standard. We note here that \textbf{map} can also be used as a first-class function in Typed Racket, and the same can be achieved with the simplified semantics using the η-expansion \mathbf{\Lambda{}}(α\ β).{\bfit λ}(x_f:(α\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}β \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})x_l:(\textbf{Listof}\ α)).(\textbf{map}\ x_f\ x_l) of the \textbf{map} operator.

\frac{\begin{gathered}\end{gathered}}{\begin{gathered}(\textbf{map}\ v_f\ \langle{}v{}_1, v{}_2\rangle{}) ↪ (\mathit{cons}\ \mathbf{(}v_f\ v{}_1\mathbf{)}\ (\textbf{map}\ v_f\ v{}_2)\end{gathered}}\ {\rm E\text{-}M{\small A}{\small P}\text{-}P{\small A}{\small I}{\small R}}

\frac{\begin{gathered}\end{gathered}}{\begin{gathered}(\textbf{map}\ v_f\ \textbf{$\mathord{{\bfit \text{null}}}$}) ↪ \textbf{$\mathord{{\bfit \text{null}}}$}\end{gathered}}\ {\rm E\text{-}M{\small A}{\small P}\text{-}N{\small U}{\small L}{\small L}}

4.2.15 Type validity rules

Polymorphic type variables valid types if they are bound, that is if they are present in the Δ environment. Additionally variadic (i.e. dotted) polymorphic type variables may be present in the environment. When this is the case, they can be used as part of a (\textbf{List}\ τ \mathbf{\ldots{}}_{α}) type.

\frac{\begin{gathered}α \in{} Δ\end{gathered}}{\begin{gathered}Δ ⊢ α\end{gathered}}\ {\rm TE\text{-}V{\small A}{\small R}}

\frac{\begin{gathered}α \mathbf{\ldots{}} \in{} Δ \\ Δ \cup \{α\} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{List}\ τ \mathbf{\ldots{}}_{α})\end{gathered}}\ {\rm TE\text{-}DL{\small I}{\small S}{\small T}}

The following rules indicate that function types are valid if their use of polymorphic type variables is well-scoped.

\frac{\begin{gathered}Δ \triangleright τ_r \mathbf{\ldots{}}_{α} \\ \overrightarrow{Δ ⊢ τ{}_i} \\ Δ ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\overrightarrow{τ{}_i}\ \ {\mathbf{.}}\ \ τ_r \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})\end{gathered}}\ {\rm TE\text{-}DF{\small U}{\small N}}

\frac{\begin{gathered}Δ \cup \{\overrightarrow{α{}_i}\} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_i})\ τ)\end{gathered}}\ {\rm TE\text{-}A{\small L}{\small L}}

\frac{\begin{gathered}Δ \cup \{\overrightarrow{α{}_i}\ β \mathbf{\ldots{}}\} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_i}\ β \mathbf{\ldots{}})\ τ)\end{gathered}}\ {\rm TE\text{-}DA{\small L}{\small L}}

\frac{\begin{gathered}α \mathbf{\ldots{}} \in{} Δ \\ Δ \cup \{α\} ⊢ τ\end{gathered}}{\begin{gathered}Δ \triangleright τ \mathbf{\ldots{}}_{α}\end{gathered}}\ {\rm TE\text{-}DP{\small R}{\small E}{\small T}{\small Y}{\small P}{\small E}}

The following rule indicates that types built using the recursive type combinator \textbf{Rec} are valid if their use of the recursive type variable r is well-scoped.

\frac{\begin{gathered}Δ \cup \{r\} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Rec}\ r\ τ)\end{gathered}}\ {\rm TE\text{-}R{\small E}{\small C}}

The next rules are trivial, and state that the base types are valid, or simply examine validity pointwise for unions, intersections, pairs, promises and filters.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ ⊤\end{gathered}}\ {\rm TE\text{-}T{\small O}{\small P}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Num}\ n)\end{gathered}}\ {\rm TE\text{-}N{\small U}{\small M}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ \mathbf{Number}\end{gathered}}\ {\rm TE\text{-}N{\small U}{\small M}{\small B}{\small E}{\small R}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ \textbf{True}\end{gathered}}\ {\rm TE\text{-}T{\small R}{\small U}{\small E}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ \textbf{False}\end{gathered}}\ {\rm TE\text{-}F{\small A}{\small L}{\small S}{\small E}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Symbol}\ s)\end{gathered}}\ {\rm TE\text{-}S{\small Y}{\small M}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ \mathbf{Symbol}\end{gathered}}\ {\rm TE\text{-}S{\small Y}{\small M}{\small B}{\small O}{\small L}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_i}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ{}_i})\end{gathered}}\ {\rm TE\text{-}U{\small N}{\small I}{\small O}{\small N}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_i}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{$\cap$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ{}_i})\end{gathered}}\ {\rm TE\text{-}I{\small N}{\small T}{\small E}{\small R}{\small S}{\small E}{\small C}{\small T}{\small I}{\small O}{\small N}}

\frac{\begin{gathered}Δ ⊢ τ \\ Δ ⊢ σ\end{gathered}}{\begin{gathered}Δ ⊢ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} σ\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\end{gathered}}\ {\rm TE\text{-}P{\small A}{\small I}{\small R}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢ \textbf{Null}\end{gathered}}\ {\rm TE\text{-}N{\small U}{\small L}{\small L}}

\frac{\begin{gathered}Δ ⊢_R R\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Promise}\ \mathrm{R})\end{gathered}}\ {\rm TE\text{-}P{\small R}{\small O}{\small M}{\small I}{\small S}{\small E}}

\frac{\begin{gathered}Δ ⊢ τ \\ Δ ⊢_{\mathrm{\phi}} \phi{}^+ \\ Δ ⊢_{\mathrm{\phi}} \phi{}^-\end{gathered}}{\begin{gathered}Δ ⊢_R {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm TE\text{-}R}

\frac{\begin{gathered}\overrightarrow{Δ ⊢_{\mathrm{ψ}} ψ}\end{gathered}}{\begin{gathered}Δ ⊢_{\mathrm{\phi}} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ}\end{gathered}}\ {\rm TE\text{-}P{\small H}{\small I}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ}\end{gathered}}{\begin{gathered}Δ ⊢_{\mathrm{ψ}} τ_{π(\mathit{loc})}\end{gathered}}\ {\rm TE\text{-}P{\small S}{\small I}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ}\end{gathered}}{\begin{gathered}Δ ⊢_{\mathrm{ψ}} \overline{τ}_{π(\mathit{loc})}\end{gathered}}\ {\rm TE\text{-}P{\small S}{\small I}\text{-}N{\small O}{\small T}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Δ ⊢_{\mathrm{ψ}} ⊥\end{gathered}}\ {\rm TE\text{-}P{\small S}{\small I}\text{-}B{\small O}{\small T}}

4.2.16 Typing rules

The rules below relate the simple expressions to their type.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{symbol}\ s) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{Symbol}\ s) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}S{\small Y}{\small M}{\small B}{\small O}{\small L}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{gensym}) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\mathbf{Symbol} \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}G{\small E}{\small N}{\small S}{\small Y}{\small M}}

\frac{\begin{gathered}Γ ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{delay}\ e) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{Promise}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}P{\small R}{\small O}{\small M}{\small I}{\small S}{\small E}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ x : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}Γ(x) \;{\mathbf{;}}\; \overline{\textbf{False}} {\mathbf{{/}}} \textbf{True} \;{\mathbf{;}}\; x{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}V{\small A}{\small R}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ p : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}δ_τ(p) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}P{\small R}{\small I}{\small M}{\small O}{\small P}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \textbf{true} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\textbf{True} \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}T{\small R}{\small U}{\small E}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \textbf{false} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\textbf{False} \;{\mathbf{;}}\; ⊥ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}F{\small A}{\small L}{\small S}{\small E}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{num}\ n) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{Num}\ n) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}N{\small U}{\small M}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \textbf{null} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\textbf{Null} \;{\mathbf{;}}\; ⊥ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}N{\small U}{\small L}{\small L}}

Below are the rules for the various flavours of lambda functions and polymorphic abstractions.

[Should the φ⁺ φ⁻ o be preserved in {\rm T\text{-}TA{\small B}{\small S}} and {\rm T\text{-}DTA{\small B}{\small S}{\small ?}}]Todo

\frac{\begin{gathered}Γ, x{}_0:σ{}_0, \overrightarrow{x{}_i:σ{}_i} ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ \phi{}^+{}’ = \phi{}^+\vphantom{\phi}{|}_{{x{}_0}↦{\bullet{}}} \\ \phi{}^-{}’ = \phi{}^-\vphantom{\phi}{|}_{{x{}_0}↦{\bullet{}}} \\ o{}’ = o\vphantom{o}{|}_{{x{}_0}↦{\bullet{}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{λ}(x{}_0:σ{}_0\ \overrightarrow{x{}_i:σ{}_i}).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\overrightarrow{σ}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+{}’ {\mathbf{{/}}} \phi{}^-{}’ \;{\mathbf{;}}\; o{}’{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}A{\small B}{\small S}P{\small R}{\small E}{\small D}}

\frac{\begin{gathered}Γ, \overrightarrow{x:σ} ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{λ}(\overrightarrow{x:σ}).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\overrightarrow{σ}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}A{\small B}{\small S}}

\frac{\begin{gathered}Γ, \overrightarrow{x:σ}, x_r:(\textbf{Listof}\ σ_r) ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{λ}(\overrightarrow{x:σ}\ \ .\ \ x_r:σ_r*).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\overrightarrow{σ}\ \ {\mathbf{.}}\ \ σ_r{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}A{\small B}{\small S}{\small *}}

\begin{aligned}\vphantom{x}&{\rm T\text{-}DA{\small B}{\small S}}\\ \vphantom{x}&\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_k} \\ Δ \triangleright τ_r \mathbf{\ldots{}}_{α} \\ Γ, \overrightarrow{x{}_k : τ{}_k}, x_r : τ_r \mathbf{\ldots{}}_{α} ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{λ}(\overrightarrow{x{}_k:τ{}_k}\ x_r:τ_r \mathbf{\ldots{}}_{α}).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\overrightarrow{τ{}_k}\ \ {\mathbf{.}}\ \ τ_r \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\end{aligned}

\frac{\begin{gathered}Γ ; Δ\cup\{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{α}\} ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{\Lambda{}}(\overrightarrow{α}).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α})\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}TA{\small B}{\small S}}

\frac{\begin{gathered}Γ ; Δ\cup\{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{α}\}\cup\{β \mathbf{\ldots{}}\} ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{\Lambda{}}(\overrightarrow{α}\ β \mathbf{\ldots{}}).e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α}\ β \mathbf{\ldots{}})\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}DTA{\small B}{\small S}}

The \vphantom{\phi}{|}_{{x}↦{z}} operation restricts the information contained within a \phi or o so that the result only contains information about the variable x, and renames it to z. When applied to a filter \phi, it corresponds to the \operatorname{abo} and \operatorname{ apo} operators from (Tobin-Hochstadt 2010), pp. 65,75.

The ⊥ cases of the \operatorname{apo} operator from (Tobin-Hochstadt 2010), pp. 65,75 are covered by the corresponding cases in the \operatorname{restrict} and \operatorname{remove} operators defined below, and therefore should not need to be included in our \vphantom{\phi}{|}_{{x}↦{z}} operator. The subst

\begin{aligned} \phi{|}_{{x}↦{z}} &= \bigcup \overrightarrow{ψ{|}_{{x}↦{z}}}&\\ ⊥{|}_{{x}↦{z}} &= \{⊥\}&\\ τ_{π(y)}\vphantom{τ}{|}_{{x}↦{z}} &= \emptyset{} &\text{ if } y \neq x \\ \overline{τ}_{π(y)}\vphantom{τ}{|}_{{x}↦{z}} &= \emptyset{} &\text{ if } y \neq x \\ τ_{π(x)}\vphantom{τ}{|}_{{x}↦{z}} &= \{τ_{π(z)}\} &\\ \overline{τ}_{π(x)}\vphantom{τ}{|}_{{x}↦{z}} &= \{\overline{τ}_{π(z)}\} & \end{aligned}

\begin{aligned} π(x){|}_{{x}↦{\emptyset{}}} &= \emptyset{} &\\ π(x){|}_{{x}↦{z}} &= π(z) &\text{ if } z \neq \emptyset{} \\ π(y){|}_{{x}↦{z}} &= \emptyset{} &\text{ if } y \neq x \\ \emptyset{}{|}_{{x}↦{z}} &= \emptyset{} & \end{aligned}

The map function can be called like any other function, but also has a specific rule allowing a more precise result type when mapping a polymorphic function over a (\textbf{List}\ τ \mathbf{\ldots{}}_{α}). ormap, andmap and apply similarly have special rules for variadic polymorphic lists. We include the rule for map below as an example. The other rules are present in (Tobin-Hochstadt 2010), pp. 96.

\frac{\begin{gathered}Γ ; Δ ⊢ e_r : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_r \mathbf{\ldots{}}_{α} \;{\mathbf{;}}\; \phi{}^+_r {\mathbf{{/}}} \phi{}^-_r \;{\mathbf{;}}\; o_r{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ Γ ; Δ ⊢ e_f : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (β)\ (τ_r[α↦β]\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})) \;{\mathbf{;}}\; \phi{}^+_f {\mathbf{{/}}} \phi{}^-_f \;{\mathbf{;}}\; o_f{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{map}\ e_f\ e_r) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ[β↦α] \mathbf{\ldots{}}_{α} \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}DM{\small A}{\small P}}

Below are the typing rules for the various flavours of function application and instantiation of polymorphic abstractions.

[For the inst rules, are the φ⁺ φ⁻ o preserved?]Todo

\frac{\begin{gathered}Γ ; Δ ⊢ e_{\mathit{op}} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_{\mathit{op}} \;{\mathbf{;}}\; \phi{}^+_{\mathit{op}} {\mathbf{{/}}} \phi{}^-_{\mathit{op}} \;{\mathbf{;}}\; o_{\mathit{op}}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ \overrightarrow{Γ ; Δ ⊢ a{}_i : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_{a{}_i} \;{\mathbf{;}}\; \phi{}^+_{a{}_i} {\mathbf{{/}}} \phi{}^-_{a{}_i} \;{\mathbf{;}}\; o_{a{}_i}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}} \\ \overrightarrow{⊢ τ_a \mathrel{≤:} τ_{\mathit{in}}} ⊢ τ_{\mathit{op}} \mathrel{≤:} (\overrightarrow{τ_{\mathit{in}}}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_r \;{\mathbf{;}}\; \phi{}^+_r {\mathbf{{/}}} \phi{}^-_r \;{\mathbf{;}}\; o_r{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \\ \phi{}^+_r{}’ = \phi{}^+_r{|}_{{\bullet{}}↦{o_{a_0}}} \\ \phi{}^-_r{}’ = \phi{}^-_r{|}_{{\bullet{}}↦{o_{a_0}}} \\ o{}’ = o{|}_{{\bullet{}}↦{o_{a_0}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ \mathbf{(}e_{\mathit{op}}\ \overrightarrow{a{}_i}\mathbf{)} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\overrightarrow{σ}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_r \;{\mathbf{;}}\; \phi{}^+{}’ {\mathbf{{/}}} \phi{}^-{}’ \;{\mathbf{;}}\; o{}’{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}A{\small P}{\small P}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_j} \\ Γ ; Δ ⊢ e_{\mathit{op}} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_j})\ τ) \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{@}\ e_{\mathit{op}}\ \overrightarrow{τ{}_j}) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ[\overrightarrow{a{}_j ↦ τ{}_j}] \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}I{\small N}{\small S}{\small T}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_j}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{Δ ⊢ τ{}_j}} \\ \overrightarrow{Δ ⊢ τ{}_k}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{Δ ⊢ τ{}_k}} \\ Γ ; Δ ⊢ e_{\mathit{op}} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_j}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{α{}_j}}\ β \mathbf{\ldots{}})\ τ) \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{@}\ e_{\mathit{op}}\ \overrightarrow{τ{}_j}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{τ{}_j}}\ \overrightarrow{τ{}_k}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{τ{}_k}}) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\mathit{td_τ}(τ[\overrightarrow{a{}_j ↦ τ{}_j}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{n}}\iflatex{n}}{\vphantom{a{}_j ↦ τ{}_j}}],\ β,\ \overrightarrow{τ{}_k}\overset{\scriptscriptstyle\,\ifmathjax{\raise1mu{m}}\iflatex{m}}{\vphantom{τ{}_k}}) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}DI{\small N}{\small S}{\small T}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_k} \\ Δ \triangleright τ_r \mathbf{\ldots{}}_{β} \\ Γ ; Δ ⊢ e_{\mathit{op}} : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α{}_k}\ α_r \mathbf{\ldots{}})\ τ) \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{@}\ e_{\mathit{op}}\ \overrightarrow{τ{}_k}\ τ_r \mathbf{\ldots{}}_{β}) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\mathit{sd}(τ[\overrightarrow{a{}_k ↦ τ{}_k}],\ α_r,\ τ_r,\ β) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ϵ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}DI{\small N}{\small S}{\small T}D}

The rule for \textbf{if} uses the information gained in the condition to narrow the type of variables in the then and else branches. This is the core rule of the occurrence typing aspect of Typed Racket.

\frac{\begin{gathered}Γ ; Δ ⊢ e{}_1 : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ{}_1 \;{\mathbf{;}}\; \phi{}^+{}_1 {\mathbf{{/}}} \phi{}^-{}_1 \;{\mathbf{;}}\; o{}_1{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ Γ ; Δ + \phi{}^+{}_1 ⊢ e{}_2 : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ{}_2 \;{\mathbf{;}}\; \phi{}^+{}_2 {\mathbf{{/}}} \phi{}^-{}_2 \;{\mathbf{;}}\; o{}_2{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ Γ ; Δ + \phi{}^-{}_1 ⊢ e{}_3 : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ{}_3 \;{\mathbf{;}}\; \phi{}^+{}_3 {\mathbf{{/}}} \phi{}^-{}_3 \;{\mathbf{;}}\; o{}_3{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ ⊢ τ{}_2 \mathrel{≤:} τ_r \\ ⊢ τ{}_3 \mathrel{≤:} τ_r \\ \phi_r{}^+ / \phi_r{}^- = \operatorname{combinefilter}(\phi{}^+{}_1 / \phi{}^-{}_1, \phi{}^+{}_2 / \phi{}^-{}_2, \phi{}^+{}_3 / \phi{}^-{}_3) \\ o_r = \begin{cases} o{}_2 & \text{ if } o{}_2 = o{}_3 \\ \emptyset{} & \text{ otherwise } \end{cases}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{if}\ e{}_1\ e{}_2\ e{}_3) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ_r \;{\mathbf{;}}\; \phi_r{}^+ {\mathbf{{/}}} \phi_r{}^- \;{\mathbf{;}}\; o_r{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}I{\small F}}

The Γ + \phi operator narrows the type of variables in the environment using the information contained within \phi.

\begin{aligned}[m] Γ + \{τ_{π(x)}\} \cup \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ} &= (Γ, x : \operatorname{update}(Γ(x), τ_π)) + \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ}\\ Γ + \{\overline{τ}_{π(x)}\} \cup \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ} &= (Γ, x : \operatorname{update}(Γ(x), \overline{τ}_π)) + \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ}\\ Γ + \{⊥\} \cup \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ} &= Γ{}’ \text{ where } \forall{}x\in{} \operatorname{dom}(Γ).⊢ Γ{}’(x) \mathrel{=:} ⊥\\ Γ + ϵ &= Γ \\ \end{aligned}

The \operatorname{update} operator propagates the information contained within a ψ down to the affected part of the type.

\begin{aligned}[m] \operatorname{update}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}, σ_{π::car} ) &= \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}\operatorname{update}(τ, σ_π){\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\\ \operatorname{update}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}, \overline{σ}_{π::car}) &= \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}\operatorname{update}(τ, \overline{σ}_π){\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\\ \operatorname{update}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}, σ_{π::cdr} ) &= \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} \operatorname{update}(τ{}’, σ_π)\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\\ \operatorname{update}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}, \overline{σ}_{π::cdr} ) &= \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} \operatorname{update}(τ{}’, \overline{σ}_π)\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\\ \operatorname{update}(τ, σ_ϵ) &= \operatorname{restrict}(τ, σ) \\ \operatorname{update}(τ, \overline{σ}_ϵ) &= \operatorname{remove}(τ, σ) \end{aligned}

The \operatorname{update} operator can then apply \operatorname{restrict} to perform the intersection of the type indicated by the \textbf{if}’s condition and the currently-known type for the subpart of the considered variable.

[How do \operatorname{restrict} and \operatorname{remove} behave on intersections?]Todo

\begin{aligned}[m] \operatorname{restrict}(τ, σ) &= ⊥ &\text{ if } \operatorname{no-overlap}(τ,σ)\\ \operatorname{restrict}((\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ}), σ) &= (\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{restrict}(τ,σ)}) &\\ \operatorname{restrict}(τ, σ) &= τ &\text{ if } ⊢ τ \mathrel{≤:} σ\\ \operatorname{restrict}(τ, σ) &= σ &\text{ otherwise } \end{aligned}

The \operatorname{update} operator can also apply the \operatorname{remove} operator when the condition determined that the subpart of the considered variable is not of a given type.

\begin{aligned}[m] \operatorname{remove}(τ, σ) &= ⊥ &\text{ if } ⊢ τ \mathrel{≤:} σ \\ \operatorname{remove}((\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ}), σ) &= (\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{remove}(τ,σ)}) &\\ \operatorname{remove}(τ, σ) &= τ &\text{ otherwise } \end{aligned}

[Δ is not available here.]Todo [The non-nested use of σ is not quite correct syntactically speaking]Todo

The \operatorname{restrict} operator and the \operatorname{simplify} operator described later both rely on \operatorname{no-overlap} to determine whether two types have no intersection, aside from the ⊥ type.

\begin{aligned}[m] \operatorname{no-overlap}(τ, τ{}’) &= \mathrm{true} &&\text{ if } \nexists σ .\begin{aligned}[t] &⊢ σ \mathrel{≤:} τ\\ {}\mathbin{∧}{} &⊢ σ \mathrel{≤:} τ{}’\\ {}\mathbin{∧}{} &Δ ⊢ σ\\ {}\mathbin{∧}{} &⊢ σ \mathrel{\neq:} ⊥\end{aligned}\\ \operatorname{no-overlap}(τ, σ) &= \mathrm{false} &&\text{ otherwise } \end{aligned}

The \operatorname{combinefilter} operator is used to combine the \phi information from the two branches of the \textbf{if} expression, based on the \phi information of the condition. This allows Typed Racket to correctly interpret and, or as well as other boolean operations, which are implemented as macros translating down to nested if conditionals. Typed Racket will therefore be able to determine that in the then branch of (if (and (string? x) (number? y)) 'then 'else), the type of x is String, and the type of y is Number. We only detail a few cases of combinefilter here, a more complete description of the operator can be found in (Tobin-Hochstadt 2010), pp. 69,75–84.

\begin{aligned}[m] \operatorname{combinefilter}(ϵ / ⊥, \phi^\pm{}{}_2, \phi^\pm{}{}_3) &= \phi^\pm{}{}_2 \\ \operatorname{combinefilter}(⊥ / ϵ, \phi^\pm{}{}_2, \phi^\pm{}{}_3) &= \phi^\pm{}{}_3 \\ \operatorname{combinefilter}(⊥ / ⊥, \phi^\pm{}{}_2, \phi^\pm{}{}_3) &= ⊥ &\\ \operatorname{combinefilter}(\phi{}^+{}_1 / \phi{}^-{}_1, \phi{}^+{}_2 / \phi{}^-{}_2, ⊥/ϵ) &= \phi{}^+{}_1 \cup \phi{}^+{}_2 \\ \operatorname{combinefilter}( \{ τ_{π(\mathit{loc})} \} \cup \phi{}^+{}_1 / \{ \overline{τ}_{π(\mathit{loc})} \} \phi{}^-{}_1, ϵ / ⊥, ⊥/ϵ) &= (\cup\ τ\ σ)_{π(\mathit{loc})} / \overline{(\cup\ τ\ σ)_{π(\mathit{loc})}} \\ \ldots{} & = \ldots{} & \\ \operatorname{combinefilter}(\phi^\pm{}{}_1, \phi^\pm{}{}_2, \phi^\pm{}{}_3) &= ϵ / ϵ \qquad \text{ otherwise } \\ \end{aligned}

4.2.17 Simplification of intersections

In some cases, intersections are simplified, and the eventual resulting ⊥ types propagate outwards through pairs (and structs, which we do not model here). The \operatorname{simplify} and \operatorname{propagate_⊥} operators show how these simplification and propagation steps are performed. The simplification step mostly consists in distributing intersections over unions and pairs, and collapsing pairs and unions which contain ⊥, for the traversed parts of the type.

\begin{aligned} \operatorname{simplify}((\textbf{$\cap$}\ τ\ τ{}’\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ{}”})) &= \operatorname{simplify}((\textbf{$\cap$}\ (\textbf{$\cap$}\ τ\ τ{}’)\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ{}”})) \\ \operatorname{simplify}((\textbf{$\cap$}\ (\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ})\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{σ})) &= \operatorname{propagate_⊥}((\textbf{$\cup$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{simplify}((\textbf{$\cap$}\ τ\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{σ}))}))\\ \operatorname{simplify}((\textbf{$\cap$}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} τ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}σ{\mathbf{,}} σ{}’\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭})) &= \operatorname{propagate_⊥}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}\operatorname{simplify}((\textbf{$\cap$}\ τ\ σ)){\mathbf{,}} \operatorname{simplify}((\textbf{$\cap$}\ τ{}’\ σ{}’))\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭})\\ \operatorname{simplify}((\textbf{$\cap$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{σ})) &= \begin{cases} ⊥ & \hspace{-1.5em}\text{ if } \exists{} τ, τ{}’ \in{} \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{σ}\} . \operatorname{no-overlap}(τ, τ{}’) \\ (\textbf{$\cap$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{simplify}(σ)}) &\hspace{-1em}\text{ otherwise } \end{cases} \end{aligned}

\operatorname{simplify}(τ) is applied pointwise in other cases:

\begin{aligned} \operatorname{simplify}((\overrightarrow{τ}\ {\mathbf{\rightarrow{}}}\ \mathrm{R})) &= (\overrightarrow{\operatorname{simplify}(τ)}\ {\mathbf{\rightarrow{}}}\ \operatorname{simplify}(\mathrm{R})) \\ \operatorname{simplify}((\overrightarrow{τ}\ \ {\mathbf{.}}\ \ τ{\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \mathrm{R})) &= (\overrightarrow{\operatorname{simplify}(τ)}\ \ {\mathbf{.}}\ \ \operatorname{simplify}(τ){\mathbf{*}}\ {\mathbf{\rightarrow{}}}\ \operatorname{simplify}(\mathrm{R}))\\ \operatorname{simplify}((\overrightarrow{τ}\ \ {\mathbf{.}}\ \ τ \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \mathrm{R})) &= (\overrightarrow{\operatorname{simplify}(τ)}\ \ {\mathbf{.}}\ \ \operatorname{simplify}(τ) \mathbf{\ldots{}}_{α}\ {\mathbf{\rightarrow{}}}\ \operatorname{simplify}(\mathrm{R}))\\ \operatorname{simplify}((\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α})\ τ)) &= (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α})\ \operatorname{simplify}(τ))\\ \operatorname{simplify}((\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α}\ α \mathbf{\ldots{}})\ τ)) &= (\textbf{${\mathbf{\forall{}}}$}\ (\overrightarrow{α}\ α \mathbf{\ldots{}})\ \operatorname{simplify}(τ))\\ \operatorname{simplify}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} σ\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}) &= \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}\operatorname{simplify}(τ){\mathbf{,}} \operatorname{simplify}(σ)\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\\ \operatorname{simplify}((\textbf{List}\ τ \mathbf{\ldots{}}_{α})) &= (\textbf{List}\ \operatorname{simplify}(τ) \mathbf{\ldots{}}_{α})\\ \operatorname{simplify}((\textbf{Promise}\ \mathrm{R})) &= (\textbf{Promise}\ \operatorname{simplify}(\mathrm{R}))\\ \operatorname{simplify}((\textbf{Rec}\ r\ τ)) &= (\textbf{Rec}\ r\ \operatorname{simplify}(τ)) \\ \operatorname{simplify}(τ) &= τ \qquad \text{ otherwise } \\ \operatorname{simplify}({\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) &= {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\operatorname{simplify}(τ) \;{\mathbf{;}}\; \operatorname{simplify}(\phi{}^+) {\mathbf{{/}}} \operatorname{simplify}(\phi{}^-) \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\\ \operatorname{simplify}(\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{ψ}) &= \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{simplify}(ψ)}\\ \operatorname{simplify}(τ_{π(loc)}) &= \operatorname{simplify}(τ)_{π(loc)}\\ \operatorname{simplify}(\overline{τ}_{π(loc)}) &= \overline{\operatorname{simplify}(τ)}_{π(loc)}\\ \operatorname{simplify}(⊥) = ⊥ \end{aligned}

\begin{aligned} \operatorname{propagate_⊥}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} σ\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}) &= ⊥ & \text{ if } ⊢ τ \mathrel{=:} ⊥\\ \operatorname{propagate_⊥}(\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}τ{\mathbf{,}} σ\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}) &= ⊥ & \text{ if } ⊢ σ \mathrel{=:} ⊥\\ \operatorname{propagate_⊥}(τ) &= ⊥ &\text{ if } ⊢ τ \mathrel{=:} ⊥\\\operatorname{propagate_⊥}(τ) &= τ &\text{ otherwise } \end{aligned}

[Apply the intersections on substituted poly types after an inst (or rely on the sutyping rule for intersections to recognise that ⊥ is a subtype of the resulting type?)]Todo.

4.2.18 δ-rules

Finally, the type and semantics of primitive functions are expressed using the δ-rules given below.

\begin{aligned} δ(\textit{add1}) = (\mathbf{Number}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\mathbf{Number} \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \\ δ(\textit{number?}) = (⊤\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}Boolean \;{\mathbf{;}}\; \mathbf{Number}_\bullet{} {\mathbf{{/}}} \overline{\mathbf{Number}}_\bullet{} \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \\ δ(\textit{pair?}) = (⊤\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}Boolean \;{\mathbf{;}}\; \ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}⊤{\mathbf{,}} ⊤\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}_\bullet{} {\mathbf{{/}}} \overline{\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}⊤{\mathbf{,}} ⊤\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}}_\bullet{} \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \\ δ(\textit{null?}) = (⊤\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}Boolean \;{\mathbf{;}}\; \textbf{Null}_\bullet{} {\mathbf{{/}}} \overline{\textbf{Null}}_\bullet{} \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}) \\ δ(\textit{identity}) = (\textbf{${\mathbf{\forall{}}}$}\ (α)\ (α\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}α \;{\mathbf{;}}\; \overline{\textbf{$\mathord{{\bfit \text{false}}}$}}_{\bullet{}} {\mathbf{{/}}} \textbf{$\mathord{{\bfit \text{false}}}$}_{\bullet{}} \;{\mathbf{;}}\; \bullet{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})) \\ δ(\mathit{cons}) = (\textbf{${\mathbf{\forall{}}}$}\ (α\ β)\ (α\ β\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}α{\mathbf{,}} β\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭} \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})) \\ δ(\textit{car}) = (\textbf{${\mathbf{\forall{}}}$}\ (α\ β)\ (\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}α{\mathbf{,}} β\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}α \;{\mathbf{;}}\; \overline{\textbf{$\mathord{{\bfit \text{false}}}$}}_{car(\bullet{})} {\mathbf{{/}}} \textbf{$\mathord{{\bfit \text{false}}}$}_{car(\bullet{})} \;{\mathbf{;}}\; car(\bullet{}){\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})) \\ δ(\textit{cdr}) = (\textbf{${\mathbf{\forall{}}}$}\ (α\ β)\ (\ifmathjax{\hspace{-0.2ex}\unicode{x276C}\hspace{-0.2ex}}\iflatex{❬}α{\mathbf{,}} β\ifmathjax{\hspace{-0.2ex}\unicode{x276D}\hspace{-0.2ex}}\iflatex{❭}\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}β \;{\mathbf{;}}\; \overline{\textbf{$\mathord{{\bfit \text{false}}}$}}_{cdr(\bullet{})} {\mathbf{{/}}} \textbf{$\mathord{{\bfit \text{false}}}$}_{cdr(\bullet{})} \;{\mathbf{;}}\; cdr(\bullet{}){\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}})) \\ \end{aligned}

4.2.19 Soundness

Since Typed Racket is an existing language which we use for our implementation, and not a new language, we do not provide here a full proof of correctness.

We invite instead the interested reader to refer to the proof sketches given in (Tobin-Hochstadt 2010), pp. 68–84. These proof sketches only cover a subset of the language presented here, namely a language with variables, function applictation, functions of a single argument, pairs, booleans, numbers and \textbf{if} conditionals with support for occurrence typing. Since occurrence typing is the main focus of the proof, the other extensions aggregated here should not significantly threaten its validity.

5 Extensible type system and algebraic datatypes

\def\ifmathjax#1{#1}\def\iflatex#1{}

5.1 Extensible type systems via type-level macros

\def\ifmathjax#1{#1}\def\iflatex#1{}

5.2 Extension of Typed Racket with algebraic datatypes and row polymorphism

\def\ifmathjax#1{#1}\def\iflatex#1{}

We extend the formalisation from (Tobin-Hochstadt 2010), pp. 62, 72 and 92.

5.2.1 Notations

We use the same notations as in Formal semantics for part of Typed Racket’s type system. Additionally, we use ρ_{c} to denote a row type variable abstracting over a set of constructors, and we use \varrho{}_{f} to denote a row type variable abstracting over a set of fields. The occurrences of c and f in this context are purely syntactical, and only serve the purpose of distinguishing between the two notations — the one for constructors, and the one for fields.

We define the universe of constructor names 𝒞 as being equivalent to the set of strings of unicode characters, and the universe of field names ℱ likewise (the distinction resides only in their intended use). Constructor and field names are compile-time constants, i.e. they are written literally in the program source.

\kappa \ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq} name \in{} 𝒞

a \ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq} name \in{} ℱ

5.2.2 Types (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

We introduce two new sorts of types: constructors and records. Constructors are similar to a Typed Racket pair whose left element is a symbol, used as a tag. A constructor’s tag does not need to be declared beforehand, and can be used on-the-fly. This makes these constructors very similar to the constructors used in CAML’s polymorphic variants (Minsky et al. 2013a), chapter 6. Records are similar to the structs available in Typed Racket, but the accessor for a field is not prefixed by the name of the struct introducing that field. This means that the same accessor can be used to access the field in all records which contain that field, whereas a different accessor would be needed for each struct type in Typed Racket. We also introduce row-polymorphic abstractions, which allow a single row type variable to range over several constructors or fields.

\begin{qaligned} σ,τ & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & (\textbf{Ctor}\ \kappa\ \mathbf{of}\ τ)\hphantom{\text{constructor}}\tag*{$\llap{\text{constructor}}$}\\ & {}\mathrel{|}{} & (\textbf{Record}\ \varsigma_{f})\hphantom{\text{possibly row-polymorphic record}}\tag*{$\llap{\text{possibly row-polymorphic record}}$}\\ & {}\mathrel{|}{} & (\textbf{${\mathbf{\forall{}}}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ τ) \hphantom{\text{row-polymorphic abstraction (constructors)}}\tag*{$\llap{\text{row-polymorphic abstraction (constructors)}}$}\\ & {}\mathrel{|}{} & (\textbf{${\mathbf{\forall{}}}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ τ) \hphantom{\text{row-polymorphic abstraction (fields)}}\tag*{$\llap{\text{row-polymorphic abstraction (fields)}}$} \end{qaligned}

We further define variants as a subset of the unions allowed by Typed Racket (including unions of the constructors defined above). Variants are equivalent to the union of their cases, but guarantee that pattern matching can always be performed (for example, it is not possible in Typed Racket to distinguish the values of two function types present in the same union, and it is therefore impossible to write a pattern matching expression which handles the two cases differently). Additionally, constraints on the absence of some constructors in the row type can be specified on variants.

\begin{qaligned} σ,τ & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & (\textbf{V}\ \varsigma_{f}) \hphantom{\text{possibly row-polymorphic variant}}\tag*{$\llap{\text{possibly row-polymorphic variant}}$} \end{qaligned}

A variant acts as the union of multiple constructor types. The variant type can also contain a row type variable ranging over constructors. A variant containing a row type variable will normally contain all the constructors used to instantiate that row. The constructors which are explicitly marked as omitted using the syntax

-\kappa are however removed from the row if present within, and the constructors explicitly marked as present using the syntax

+\kappa\ \mathbf{of}\ τ will always be members of the variant. If such a constructor was present in the row with a different type, it is replaced by a constructor wrapping a value of the explicitly specified type.

\begin{qaligned} \varsigma_{c} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\kappa\ \mathbf{of}\ τ}\hphantom{\text{fixed constructors}}\tag*{$\llap{\text{fixed constructors}}$}\\ & {}\mathrel{|}{} & ρ_{c}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-\kappa{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+\kappa{}_j\ \mathbf{of}\ τ{}_j} \hphantom{\text{row without some ctors, with extra ctors}}\tag*{$\llap{\text{row without some ctors, with extra ctors}}$} \end{qaligned}

Similarly, records can contain a set of fields. It is also possible to use a row type variable ranging over constructors. The syntax -a indicates a field which could be present in the row and but will not be present in the record type, and the syntax +a:τ indicates a field which will always be present, as well as its type.

\begin{qaligned} \varsigma_{f} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a:τ}\hphantom{\text{fixed fields}}\tag*{$\llap{\text{fixed fields}}$}\\ & {}\mathrel{|}{} & \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_j:τ{}_j} \hphantom{\text{row without some fields, with extra fields}}\tag*{$\llap{\text{row without some fields, with extra fields}}$} \end{qaligned}

5.2.3 Expressions (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

We extend the syntax of expressions in typed racket as defined by (Tobin-Hochstadt 2010), pp. 62, 72 and 92 and presented in Formal semantics for part of Typed Racket’s type system by adding expressions related to constructors. The first syntax builds an instance of the constructor with label \kappa and the value of e. The expression (\kappa\textbf{?} e) determines whether e is an instance of the constructor with label \kappa. The expression (\mathbf{getval}_\kappa e) extracts the value stored in an instance of a constructor.

We also introduce expressions related to records. The first builds an instance of a record with the given fields. We note that the order in which the fields appear affects the order in which the sub-expressions will be evaluated. However, in the resulting value and in its type, the order of the fields is irrelevant. The second expression tests whether e is an instance of a record with the given fields present. The third expression is similar, but allows any number of extra fields to be present, while checking that the -a{}_j fields are absent. The fourth expression accesses the value of the a field stored in the given instance. The fifth expression updates an existing record instance by adding (or replacing) the field a, while the sixth removes the a field.

\begin{qaligned} e & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \rlap{\ldots{}}\hphantom{\!\begin{array}{l}\ldots{}\\(\textbf{ctor}\ \kappa\ e)\hphantom{\text{constructor instance}}\\(\kappa\textbf{?}\ e)\hphantom{\text{constructor predicate}}\\(\mathbf{getval}_\kappa\ e)\hphantom{\text{constructor value access}}\\\ldots{}\\(\textbf{record}\ \overrightarrow{a{}_i↦e{}_i})\hphantom{\text{record instance}}\\((\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i})\ e)\hphantom{\text{record predicate}}\\((\textbf{record$\mathbf{*}$?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j})\ e) \hphantom{\text{row-record predicate}}\\e.a\hphantom{\text{record field access}}\\e \textbf{ with } a = e\hphantom{\text{record update (new/change field)}}\\e \textbf{ without } a\hphantom{\text{record update (remove field)}}\\\ldots{}\\(\textbf{$\Lambda{}$${}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ e) \hphantom{\text{row-polymorphic abstraction (constructors)}}\\(\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ e) \hphantom{\text{row-polymorphic abstraction (fields)}}\\(\textbf{@${}_{\textbf{c}}$}\ e\ \overrightarrow{\varsigma_{c}}) \hphantom{\text{row-polymorphic instantiation (constructors)}}\\(\textbf{@${}_{\textbf{f}}$}\ e\ \overrightarrow{\varsigma_{f}}) \hphantom{\text{row-polymorphic instantiation (fields)}}\end{array}\!}\\ & {}\mathrel{|}{} & (\textbf{record}\ \overrightarrow{a{}_i↦e{}_i})\hphantom{\text{record instance}}\tag*{$\llap{\text{record instance}}$}\\ & {}\mathrel{|}{} & ((\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i})\ e)\hphantom{\text{record predicate}}\tag*{$\llap{\text{record predicate}}$}\\ & {}\mathrel{|}{} & ((\textbf{record$\mathbf{*}$?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j})\ e) \hphantom{\text{row-record predicate}}\tag*{$\llap{\text{row-record predicate}}$}\\ & {}\mathrel{|}{} & e.a\hphantom{\text{record field access}}\tag*{$\llap{\text{record field access}}$}\\ & {}\mathrel{|}{} & e \textbf{ with } a = e\hphantom{\text{record update (new/change field)}}\tag*{$\llap{\text{record update (new/change field)}}$}\\ & {}\mathrel{|}{} & e \textbf{ without } a\hphantom{\text{record update (remove field)}}\tag*{$\llap{\text{record update (remove field)}}$} \end{qaligned}

Finally, we define the row-polymorphic abstractions (\textbf{$\Lambda{}$${}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ e) and (\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ e) which bind row type variables hiding constructors and fields respectively. The corresponding instantiation operators are (\textbf{@${}_{\textbf{c}}$}\ e\ \overrightarrow{\varsigma_{c}}) and (\textbf{@${}_{\textbf{f}}$}\ e\ \overrightarrow{\varsigma_{f}}).

\begin{qaligned} e & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \rlap{\ldots{}}\hphantom{\!\begin{array}{l}\ldots{}\\(\textbf{ctor}\ \kappa\ e)\hphantom{\text{constructor instance}}\\(\kappa\textbf{?}\ e)\hphantom{\text{constructor predicate}}\\(\mathbf{getval}_\kappa\ e)\hphantom{\text{constructor value access}}\\\ldots{}\\(\textbf{record}\ \overrightarrow{a{}_i↦e{}_i})\hphantom{\text{record instance}}\\((\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i})\ e)\hphantom{\text{record predicate}}\\((\textbf{record$\mathbf{*}$?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j})\ e) \hphantom{\text{row-record predicate}}\\e.a\hphantom{\text{record field access}}\\e \textbf{ with } a = e\hphantom{\text{record update (new/change field)}}\\e \textbf{ without } a\hphantom{\text{record update (remove field)}}\\\ldots{}\\(\textbf{$\Lambda{}$${}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ e) \hphantom{\text{row-polymorphic abstraction (constructors)}}\\(\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ e) \hphantom{\text{row-polymorphic abstraction (fields)}}\\(\textbf{@${}_{\textbf{c}}$}\ e\ \overrightarrow{\varsigma_{c}}) \hphantom{\text{row-polymorphic instantiation (constructors)}}\\(\textbf{@${}_{\textbf{f}}$}\ e\ \overrightarrow{\varsigma_{f}}) \hphantom{\text{row-polymorphic instantiation (fields)}}\end{array}\!}\\ & {}\mathrel{|}{} & (\textbf{$\Lambda{}$${}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ e) \hphantom{\text{row-polymorphic abstraction (constructors)}}\tag*{$\llap{\text{row-polymorphic abstraction (constructors)}}$}\\ & {}\mathrel{|}{} & (\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ e) \hphantom{\text{row-polymorphic abstraction (fields)}}\tag*{$\llap{\text{row-polymorphic abstraction (fields)}}$}\\ & {}\mathrel{|}{} & (\textbf{@${}_{\textbf{c}}$}\ e\ \overrightarrow{\varsigma_{c}}) \hphantom{\text{row-polymorphic instantiation (constructors)}}\tag*{$\llap{\text{row-polymorphic instantiation (constructors)}}$}\\ & {}\mathrel{|}{} & (\textbf{@${}_{\textbf{f}}$}\ e\ \overrightarrow{\varsigma_{f}}) \hphantom{\text{row-polymorphic instantiation (fields)}}\tag*{$\llap{\text{row-polymorphic instantiation (fields)}}$} \end{qaligned}

5.2.4 Values (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

\begin{qaligned} v & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & (\textbf{$\mathord{{\bfit \text{ctor}}}$}\ \kappa\ v)\hphantom{\text{constructor instance}}\tag*{$\llap{\text{constructor instance}}$}\\ & {}\mathrel{|}{} & (\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i})\hphantom{\text{record instance}}\tag*{$\llap{\text{record instance}}$} \end{qaligned}

5.2.5 Evaluation contexts (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

\begin{qaligned} E & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & (\textbf{ctor}\ \kappa\ E)\hphantom{\text{constructor instance}}\tag*{$\llap{\text{constructor instance}}$}\\ & {}\mathrel{|}{} & (\kappa\textbf{?}\ E)\hphantom{\text{constructor predicate}}\tag*{$\llap{\text{constructor predicate}}$}\\ & {}\mathrel{|}{} & (\mathbf{getval}_\kappa\ E)\hphantom{\text{constructor value access}}\tag*{$\llap{\text{constructor value access}}$}\\ & {}\mathrel{|}{} & (\textbf{record}\ \overrightarrow{a{}_i = v{}_i}\ a{}_j = E\ \overrightarrow{a{}_k = e{}_k})\hphantom{\text{record instance}}\tag*{$\llap{\text{record instance}}$}\\ & {}\mathrel{|}{} & ((\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i})\ E)\hphantom{\text{record predicate}}\tag*{$\llap{\text{record predicate}}$}\\ & {}\mathrel{|}{} & ((\textbf{record$\mathbf{*}$?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j})\ E) \hphantom{\text{row-polymorphic record predicate}}\tag*{$\llap{\text{row-polymorphic record predicate}}$}\\ & {}\mathrel{|}{} & E.a\hphantom{\text{record field access}}\tag*{$\llap{\text{record field access}}$}\\ & {}\mathrel{|}{} & E \textbf{ with } a = e\hphantom{\text{record update (new/change)}}\tag*{$\llap{\text{record update (new/change)}}$}\\ & {}\mathrel{|}{} & v \textbf{ with } a = E\\ & {}\mathrel{|}{} & E \textbf{ without } a\hphantom{\text{record update (remove)}}\tag*{$\llap{\text{record update (remove)}}$} \end{qaligned}

5.2.6 Type validity rules (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

\frac{\begin{gathered}Δ \cup \{ \overrightarrow{ρ_{c}} \} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{${\mathbf{\forall{}}}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ τ)\end{gathered}}\ {\rm TE\text{-}CA{\small L}{\small L}}

\frac{\begin{gathered}Δ \cup \{ \overrightarrow{\varrho{}_{f}} \} ⊢ τ\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{${\mathbf{\forall{}}}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}})\ τ)\end{gathered}}\ {\rm TE\text{-}FA{\small L}{\small L}}

\frac{\begin{gathered}ρ_{c} \in{} Δ \\ \overrightarrow{Δ ⊢ τ{}_i} \\ \operatorname{AllDifferent}(\overrightarrow{\kappa{}_i} \overrightarrow{\kappa{}_j})\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{V}\ ρ_{c}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-(\textbf{Ctor}\ \kappa\ {}_i)}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+(\textbf{Ctor}\ \kappa{}_j\ \mathbf{of}\ τ{}_j)})\end{gathered}}\ {\rm TE\text{-}CV{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}}

\frac{\begin{gathered}\varrho{}_{f} \in{} Δ \\ \operatorname{AllDifferent}(\overrightarrow{a{}_i} \overrightarrow{a{}_j}) \\ \overrightarrow{Δ ⊢ τ{}_j}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_j:τ{}_j})\end{gathered}}\ {\rm TE\text{-}FR{\small E}{\small C}{\small O}{\small R}{\small D}}

where

\begin{aligned} \operatorname{AllDifferent}(\overrightarrow{y}) &= \mathrm{true} \text{ if } \forall{} i \neq j . y{}_i \neq y{}_j \\ \operatorname{AllDifferent}(\overrightarrow{y}) &= \mathrm{false} \text{ otherwise } \end{aligned}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ{}_i} \\ \operatorname{AllDifferent}(\overrightarrow{\kappa{}_i})\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{V}\ \overrightarrow{(\textbf{Ctor}\ \kappa{}_i\ \mathbf{of}\ τ{}_i)})\end{gathered}}\ {\rm TE\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}}

\frac{\begin{gathered}\operatorname{AllDifferent}(\overrightarrow{a{}_i}) \\ \overrightarrow{Δ ⊢ τ{}_i}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Record}\ \overrightarrow{a{}_i : τ{}_i})\end{gathered}}\ {\rm TE\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}}

\frac{\begin{gathered}\overrightarrow{Δ ⊢ τ}\end{gathered}}{\begin{gathered}Δ ⊢ (\textbf{Ctor}\ \kappa\ \mathbf{of}\ τ)\end{gathered}}\ {\rm TE\text{-}C{\small T}{\small O}{\small R}}

5.2.7 Subtyping (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

Variants which do not involve a row type are nothing more than a syntactic restriction on a union of types. The variant only allows constructors to be present in the union, as specified by the type validity rule {\rm TE\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}}.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}⊢ (\textbf{V}\ \overrightarrow{τ}) \mathrel{=:} (\textbf{$\cup$}\ \overrightarrow{τ})\end{gathered}}\ {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}\text{-}U{\small N}{\small I}{\small O}{\small N}}

From {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}\text{-}U{\small N}{\small I}{\small O}{\small N}}, we can derive that the empty variant is equivalent to the bottom type.

\begin{array}[b]{c} \begin{array}[b]{c} {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}\text{-}U{\small N}{\small I}{\small O}{\small N}}\quad{}{\rm S\text{-}B{\small O}{\small T}} \\\hline {\rm S\text{-}E{\small Q}\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}} \end{array} \\\hline ⊢ (\textbf{V}) \mathrel{=:} ⊥ \end{array} \ \smash{ \begin{array}[c]{c} {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}\text{-}E{\small M}{\small P}{\small T}{\small Y}} \\[1ex] \vphantom{⊢ (\textbf{V}) \mathrel{=:} ⊥} \end{array}}

\begin{array}[b]{c} \begin{array}[b]{c} \begin{array}[b]{c} \begin{array}[b]{c} ⊢ τ \mathrel{=:} τ{}’ \\\hline {\rm S\text{-}E{\small Q}}_1 \end{array} \quad{}\begin{array}[b]{c} ⊢ τ{}’ \mathrel{=:} τ{}” \\\hline {\rm S\text{-}E{\small Q}}_1 \end{array} \\\hline {\rm S\text{-}E{\small Q}\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}} \end{array} \quad{}\begin{array}[b]{c} \begin{array}[b]{c} ⊢ τ{}’ \mathrel{=:} τ{}” \\\hline {\rm S\text{-}E{\small Q}}_2 \end{array} \quad{}\begin{array}[b]{c} ⊢ τ \mathrel{=:} τ{}’ \\\hline {\rm S\text{-}E{\small Q}}_2 \end{array} \\\hline {\rm S\text{-}E{\small Q}\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}} \end{array} \\\hline {\rm S\text{-}E{\small Q}}_3 \end{array} \\\hline ⊢ τ \mathrel{=:} τ{}” \end{array} \ \smash{ \begin{array}[c]{c} {\rm S\text{-}E{\small Q}\text{-}T{\small R}{\small A}{\small N}{\small S}{\small I}{\small T}{\small I}{\small V}{\small E}} \\[1ex] \vphantom{⊢ τ \mathrel{=:} τ{}”} \end{array}}

\frac{\begin{gathered}\exists{} i . ⊢ τ \mathrel{≤:} σ{}_i\end{gathered}}{\begin{gathered}⊢ τ \mathrel{≤:} (\textbf{V}\ \overrightarrow{σ{}_i})\end{gathered}}\ {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}S{\small U}{\small P}{\small E}{\small R}}

\frac{\begin{gathered}\overrightarrow{⊢ τ{}_i \mathrel{≤:} σ}\end{gathered}}{\begin{gathered}⊢ (\textbf{V}\ \overrightarrow{τ{}_i}) \mathrel{≤:} σ\end{gathered}}\ {\rm S\text{-}V{\small A}{\small R}{\small I}{\small A}{\small N}{\small T}S{\small U}{\small B}}

\frac{\begin{gathered}⊢ τ \mathrel{≤:} τ{}’\end{gathered}}{\begin{gathered}⊢ (\textbf{Ctor}\ \kappa\ \mathbf{of}\ τ) \mathrel{≤:} (\textbf{Ctor}\ \kappa\ \mathbf{of}\ τ{}’)\end{gathered}}\ {\rm S\text{-}C{\small T}{\small O}{\small R}}

\frac{\begin{gathered}\overrightarrow{⊢ τ{}_i \mathrel{≤:} τ{}’{}_i}\end{gathered}}{\begin{gathered}⊢ (\textbf{Record}\ \overrightarrow{a{}_i : τ{}_i}) \mathrel{≤:} (\textbf{Record}\ \overrightarrow{a{}_i : τ{}’{}_i})\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}}

\frac{\begin{gathered}\overrightarrow{⊢ τ{}_j \mathrel{≤:} τ{}’{}_j}\end{gathered}}{\begin{gathered}⊢ (\textbf{Record}\ \overrightarrow{a{}_j : τ{}_j}) \mathrel{≤:} (\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_j:τ{}’{}_j})\end{gathered}}\ {\rm S\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}F}

\begin{aligned}\vphantom{x}&{\rm S\text{-}FR{\small E}{\small C}{\small O}{\small R}{\small D}F}\\ \vphantom{x}&\frac{\begin{gathered}\overrightarrow{⊢ τ{}_k \mathrel{≤:} τ{}’{}_k}\end{gathered}}{\begin{gathered}⊢ (\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_k:τ{}_k}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_l:τ{}_l}) \mathrel{≤:} (\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_k:τ{}’{}_k})\end{gathered}}\end{aligned}

\frac{\begin{gathered}⊢ τ[\overrightarrow{\varrho{}_{f}{}_i ↦ \varrho{}_{f}{}’{}_i}] \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{${\mathbf{\forall{}}}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}{}_i})\ τ) \mathrel{≤:} (\textbf{${\mathbf{\forall{}}}_{\textbf{f}}$}\ (\overrightarrow{\varrho{}_{f}{}’{}_i})\ σ)\end{gathered}}\ {\rm S\text{-}P{\small O}{\small L}{\small Y}F\text{-}}α{\rm \text{-}E{\small Q}{\small U}{\small I}{\small V}}

\frac{\begin{gathered}⊢ τ[\overrightarrow{ρ_{c}{}_i ↦ ρ_{c}{}’{}_i}] \mathrel{≤:} σ\end{gathered}}{\begin{gathered}⊢ (\textbf{${\mathbf{\forall{}}}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}{}_i})\ τ) \mathrel{≤:} (\textbf{${\mathbf{\forall{}}}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}{}’{}_i})\ σ)\end{gathered}}\ {\rm S\text{-}P{\small O}{\small L}{\small Y}C\text{-}}α{\rm \text{-}E{\small Q}{\small U}{\small I}{\small V}}

[propagate our types up/down unions like the primitive ones (I think Typed Racket does not do this everywhere it “should”).]Todo

5.2.8 Path elements (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

[Does this need any change when adding row typing?]Todo

\begin{qaligned} \mathit{pe} & {}\ifmathjax{\mathrel{{\raise0.9mu{::}\hspace{-4mu}=}}}\iflatex{\Coloneqq}{} & \ldots{}\\ & {}\mathrel{|}{} & \textbf{getval} \hphantom{\text{value of constructor}}\tag*{$\llap{\text{value of constructor}}$}\\ & {}\mathrel{|}{} & a \hphantom{\text{value of field $a$}}\tag*{$\llap{\text{value of field $a$}}$} \end{qaligned}

We extend the metafunctions for paths given in (Tobin-Hochstadt 2010), pp. 65 and 75. The \operatorname{update} metafunction is used when using filters to restrict the type of a (subpart of a) local variable in the then and else branches of a conditional.

[∷ is not defined in (Tobin-Hochstadt 2010), we have to define it.]Todo

[How should I note cleanly these removals / replacements which refer to an a and its τ or v inside the set of a{}_i?]Todo

[Also write down the simple "update" cases for row polymorphism]Todo

\begin{aligned}[m] \operatorname{update}((\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}_i}), σ_{π::a{}_j}) &= (\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}_i} ∖ \{a{}_j : τ{}_j\}\ a{}_j : \operatorname{update}(τ{}_j, σ_π)) \\ \operatorname{update}((\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}_i}), \overline{σ}_{π::a{}_j}) &= (\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}_i} ∖ \{a{}_j : τ{}_j\}\ a{}_j : \operatorname{update}(τ{}_j, \overline{σ}_π)) \\ &\quad \text{ where } a{}_j : τ{}_j \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}_i}\\ \operatorname{update}((\textbf{Ctor}\ \kappa\ τ), σ_{π::\textbf{getval}}) &= (\textbf{Ctor}\ \kappa\ \operatorname{update}(τ, σ_π))\\ \end{aligned}

\operatorname{restrict}((\textbf{V}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ}), σ) = (\textbf{V}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{restrict}(τ,σ)})

\begin{multline} \operatorname{restrict}\left( \begin{array}{l} (\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_l : τ{}_l}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_m : τ{}_m}), \\(\textbf{Record}\ \varrho{}_{f}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_k}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_l : σ{}_l}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_n : σ{}_n})\end{array}\right) \\ = (\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_k}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_l : \operatorname{update}(τ{}_l, σ{}_l)}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_m : τ{}_m}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{+a{}_n : σ{}_n}) \end{multline}

\text{ where } \operatorname{DisjointSets}( \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\}, \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_j}\}, \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_k}\}, \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_l}\}, \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_m}\}, \{\def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_n}\})

where

\begin{aligned}[m] \operatorname{DisjointSets}(\overrightarrow{s}) &= \mathrm{true} \text{ if } \forall{} s{}_i, s{}_j \in{} s . i \neq j \Rightarrow{} s{}_i \cap s{}_j = \emptyset{}\\ \operatorname{DisjointSets}(\overrightarrow{s}) &= \mathrm{false} \text{ otherwise } \end{aligned}

\begin{aligned}[m] \operatorname{remove}((\textbf{V}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{τ}), σ) &= (\textbf{V}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{\operatorname{remove}(τ,σ)}) \end{aligned}

5.2.9 Typing rules (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

[Should the filter be something else than ϵ|ϵ or is the filter inferred via other rules when the “function” does not do anything special?]Todo

\frac{\begin{gathered}Γ ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\textbf{ctor}\ \kappa\ e) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{Ctor}\ \kappa\ \mathbf{of}\ τ) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}C{\small T}{\small O}{\small R}\text{-}B{\small U}{\small I}{\small L}{\small D}}

\operatorname{applyfilter} is defined in (Tobin-Hochstadt 2010), p. 75.

[Copy the definition of applyfilter.]Todo

\frac{\begin{gathered}Γ ; Δ ⊢ e : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}τ \;{\mathbf{;}}\; \phi{}^+ {\mathbf{{/}}} \phi{}^- \;{\mathbf{;}}\; o{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}} \\ \phi{}^+_r / \phi{}^-_r = \operatorname{applyfilter}((\textbf{Ctor}\ \kappa\ \mathbf{of}\ ⊤)/\overline{(\textbf{Ctor}\ \kappa\ \mathbf{of}\ ⊤)}, τ, o)\end{gathered}}{\begin{gathered}Γ ; Δ ⊢ (\kappa\textbf{?}\ e) : {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}Boolean \;{\mathbf{;}}\; \phi{}^+_r {\mathbf{{/}}} \phi{}^-_r \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}\end{gathered}}\ {\rm T\text{-}C{\small T}{\small O}{\small R}\text{-}P{\small R}{\small E}{\small D}}

\frac{\begin{gathered}Γ ⊢ e : τ ; \phi ; o \\ τ <: (\textbf{Ctor}\ \kappa\ τ{}’) \\ o_r = \left\{ \begin{array}{rl} \textbf{getval}(π(x)) & \text{ if } o = π(x) \\ \emptyset{} & \text{ otherwise } \end{array}\right. \\ \phi_r = \operatorname{applyfilter}(\overline{\#f}_{\textbf{getval}}|\#f_{\textbf{getval}}, τ, o)\end{gathered}}{\begin{gathered}Γ ⊢ (\mathbf{getval}_\kappa\ e) : τ{}’ ; \phi_r ; o_r\end{gathered}}\ {\rm T\text{-}C{\small T}{\small O}{\small R}\text{-}V{\small A}{\small L}}

\frac{\begin{gathered}\overrightarrow{Γ ⊢ e{}_i : τ{}_i ; \phi{}_i ; o{}_i}\end{gathered}}{\begin{gathered}Γ ⊢ (\textbf{record}\ \overrightarrow{a{}_i = e{}_i}) : (\textbf{Record}\ \overrightarrow{a{}_i : τ{}_i}); ϵ|⊥ ; \emptyset{}\end{gathered}}\ {\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}B{\small U}{\small I}{\small L}{\small D}}

\frac{\begin{gathered}Γ ⊢ e : τ ; \phi ; o \\ \phi_r = \operatorname{applyfilter}((\textbf{Record}\ \overrightarrow{a{}_i : ⊤}) |\overline{(\textbf{Record}\ \overrightarrow{a{}_i : ⊤})}, τ, o)\end{gathered}}{\begin{gathered}Γ ⊢ ((\textbf{record?}\ \overrightarrow{a{}_i}) e) : Boolean ; \phi_r ; \emptyset{}\end{gathered}}\ {\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}P{\small R}{\small E}{\small D}}

\frac{\begin{gathered}Γ ⊢ e : τ ; \phi ; o \\ τ <: (\textbf{Record}\ \overrightarrow{a{}_i : τ{}_i}\ \varrho{}_{f}) \\ o_r = \left\{ \begin{array}{rl} \mathbf{a{}_j}(π(x)) & \text{ if } o = π(x) \\ \emptyset{} & \text{ otherwise } \end{array}\right. \\ \phi_r = \operatorname{applyfilter}(\overline{\#f}_{\mathbf{a{}_j}}|\#f_{\mathbf{a{}_j}}, τ, o)\end{gathered}}{\begin{gathered}Γ ⊢ e.a{}_j : τ{}’ ; \phi_r ; o_r\end{gathered}}\ {\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}G{\small E}{\small T}F{\small I}{\small E}{\small L}{\small D}}

\frac{\begin{gathered}Γ ⊢ e_{r} : τ_{r} ; \phi_{r} ; o_{r} \\ τ_{r} <: (\textbf{Record}\ \overrightarrow{a{}_i : τ{}’{}_i}\ \varrho{}_{f} - \{\overrightarrow{a{}’{}_j}\})\\Γ ⊢ e_{v} : τ_{v} ; \phi_{v} ; o_{v} \\ a ∉ \{a{}_i\} \\ a \in{} \{\overrightarrow{a{}’{}_j}\}\end{gathered}}{\begin{gathered}Γ ⊢ e_{r} \textbf{ with } a = e_{v} : (\textbf{Record}\ \overrightarrow{a{}_i : τ{}’{}_i}\ a : τ_{v}\ \varrho{}_{f} - \{\overrightarrow{a{}’{}_j}\}); ϵ|⊥ ; \emptyset{}\end{gathered}}\ {\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}}_1

TODO: removing fields on the ρ should not matter if the fields are present in the main part of the record (as they are implicitly not in the ρ, because they are in the main part).

\begin{aligned}\vphantom{x}&{\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}}_2\\ \vphantom{x}&\frac{\begin{gathered}Γ ⊢ e_{r} : τ_{r} ; \phi_{r} ; o_{r} \\ τ_{r} <: (\textbf{Record}\ \overrightarrow{a{}_i : τ{}’{}_i}\ \varrho{}_{f}) \\Γ ⊢ e_{v} : τ_{v} ; \phi_{v} ; o_{v} \\ a{}_j : τ{}’{}_j \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}’{}_i}\end{gathered}}{\begin{gathered}Γ ⊢ e_{r} \textbf{ with } a{}_j = e_{v} : (\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}’{}_i} ∖ \{a{}_j : τ{}’{}_j\}\ a{}_j : τ_{v}\ \varrho{}_{f}); ϵ|⊥ ; \emptyset{}\end{gathered}}\end{aligned}

\begin{aligned}\vphantom{x}&{\rm T\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}{\small O}{\small U}{\small T}}\\ \vphantom{x}&\frac{\begin{gathered}Γ ⊢ e_{r} : τ_{r} ; \phi_{r} ; o_{r} \\ τ_{r} <: (\textbf{Record}\ \overrightarrow{a{}_i : τ{}’{}_i}\ \varrho{}_{f}) \\ a{}_j : τ{}’{}_j \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}’{}_i}\end{gathered}}{\begin{gathered}Γ ⊢ e_{r} \textbf{ without } a : (\textbf{Record}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i : τ{}’{}_i} ∖ \{a{}_j : τ{}’{}_j\}\ \varrho{}_{f} - a) ; ϵ|⊥ ; \emptyset{}\end{gathered}}\end{aligned}

5.2.10 Operational Semantics (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

Instantiation of the new sorts of polymorphic abstractions is a no-op at run-time, similarly to those of Typed Racket.

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{@${}_{\textbf{c}}$}\ (\textbf{$\Lambda{}$${}_{\textbf{c}}$}\ (\overrightarrow{ρ_{c}})\ e)\ \overrightarrow{\varsigma_{c}}) ↪ e\end{gathered}}\ {\rm E\text{-}I{\small N}{\small S}{\small T}\text{-}C}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{@${}_{\textbf{f}}$}\ (\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\overrightarrow{ρ_{c}})\ e)\ \overrightarrow{\varsigma_{f}}) ↪ e\end{gathered}}\ {\rm E\text{-}I{\small N}{\small S}{\small T}\text{-}F}

[Does this need any change when adding row typing (they don’t add any rules in (Tobin-Hochstadt 2010))?]Todo

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{ctor}\ \kappa\ v) ↪ (\textbf{$\mathord{{\bfit \text{ctor}}}$}\ \kappa\ v)\end{gathered}}\ {\rm E\text{-}C{\small T}{\small O}{\small R}\text{-}B{\small U}{\small I}{\small L}{\small D}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\kappa\textbf{?} v) ↪ δ(\kappa\textbf{?}, v)\end{gathered}}\ {\rm E\text{-}C{\small T}{\small O}{\small R}\text{-}P{\small R}{\small E}{\small D}}

We extend the δ relation to accept in its first position not only constant functions (members of c), but also members of families of operators indexed by a constructor label or a field label, like \kappa\textbf{?}, \mathbf{getval}_\kappa and (\textbf{record?}\ \overrightarrow{a{}_i})

\begin{aligned}[m] δ(\kappa\textbf{?}, v) &= \#t &\text{ if } v = (\textbf{$\mathord{{\bfit \text{ctor}}}$}\ \kappa\ v{}’) \\ δ(\kappa\textbf{?}, v) &= \#f &\text{ otherwise } \\ \end{aligned}

[Is it really necessary to use a δ-rule for E-Ctor-GetVal ?]Todo

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\mathbf{getval}_\kappa v) ↪ δ(\mathbf{getval}_\kappa, v)\end{gathered}}\ {\rm E\text{-}C{\small T}{\small O}{\small R}\text{-}G{\small E}{\small T}V{\small A}{\small L}}

\begin{aligned}[m] δ(\mathbf{getval}_\kappa, (\textbf{$\mathord{{\bfit \text{ctor}}}$}\ \kappa\ v{}’)) & = v{}’ \end{aligned}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}(\textbf{record}\ \overrightarrow{a{}_i = v{}_i}) ↪ (\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i})\end{gathered}}\ {\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}B{\small U}{\small I}{\small L}{\small D}}

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}((\textbf{record?}\ \overrightarrow{a{}_i}) v) ↪ δ((\textbf{record?}\ \overrightarrow{a{}_i}), v)\end{gathered}}\ {\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}P{\small R}{\small E}{\small D}}

\begin{aligned}[m] δ((\textbf{record?}\ \overrightarrow{a{}_i}), v) &= \#t \text{ if } v = (\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_j = v{}_j}) ∧ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_j} = \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i} \\ δ((\textbf{record?}\ \overrightarrow{a{}_i}), v) &= \#f \text{ otherwise } \end{aligned}

\frac{\begin{gathered}a{}’ \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i} \\ a{}’ = a{}_j\end{gathered}}{\begin{gathered}(\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i}).a{}’ ↪ v{}_j\end{gathered}}\ {\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}G{\small E}{\small T}F{\small I}{\small E}{\small L}{\small D}}

[This ∖ does not make sense because we remove the label a’ from a set of label+value tuples. We must define a separate mathematical operator for removal of a label+value tuple from a set based on the label.]Todo

\begin{aligned}\vphantom{x}&{\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}}_1\\ \vphantom{x}&\frac{\begin{gathered}a{}_j \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\end{gathered}}{\begin{gathered}(\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i}) \textbf{ with } a{}_j = v{}’ ↪ (\textbf{$\mathord{{\bfit \text{record}}}$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i = v{}_i} ∖ \{a{}_j = v{}_j\}\ \quad a{}_j = v{}’) \\ (a{}_j = v{}_j) \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i = v{}_i}\end{gathered}}\end{aligned}

[what to do with the = sign? The a = v sign is syntactical, but could easily be understood as a meta comparison, instead of indicating the association between the field and the value.]Todo

\frac{\begin{gathered}a{}’ ∉ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\end{gathered}}{\begin{gathered}(\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i}) \textbf{ with } a{}’ = v{}’ ↪ (\textbf{$\mathord{{\bfit \text{record}}}$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i = v{}_i}\ \quad a{}’ = v{}’)\end{gathered}}\ {\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}}_2

\begin{aligned}\vphantom{x}&{\rm E\text{-}R{\small E}{\small C}{\small O}{\small R}{\small D}\text{-}W{\small I}{\small T}{\small H}{\small O}{\small U}{\small T}}\\ \vphantom{x}&\frac{\begin{gathered}a{}_j \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\end{gathered}}{\begin{gathered}(\textbf{$\mathord{{\bfit \text{record}}}$}\ \overrightarrow{a{}_i = v{}_i}) \textbf{ without } a{}_j ↪ (\textbf{$\mathord{{\bfit \text{record}}}$}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i = v{}_i} ∖ \{a{}_j = v{}_j\}) \\ (a{}_j = v{}_j) \in{} \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i = v{}_i}\end{gathered}}\end{aligned}

5.2.11 Shorthands (with ρ)

\def\ifmathjax#1{#1}\def\iflatex#1{}

The polymorphic builder function for the \kappa constructor which intuitively corresponds to (\textbf{ctor}\ \kappa) can be written as the η-expansion of the (\textbf{ctor}\ \kappa\ e) operator:

\mathbf{\Lambda{}}(α).\mathbf{λ}(x : α).(\textbf{ctor}\ \kappa\ x)

The same applies to the predicate form of constructors:

\mathbf{λ}(x : ⊤).\mathbf{(}\kappa\textbf{?}\ x\mathbf{)}

The same applies to the accessor for a constructor’s encapsulated value:

\mathbf{\Lambda{}}(α).\mathbf{λ}(x : (\textbf{Ctor}\ \kappa\ α)).\mathbf{(}\mathbf{getval}_\kappa\ x\mathbf{)}

As a convenience, we will write (\textbf{ctor}\ \kappa), \kappa\textbf{?} and \mathbf{getval}_\kappa as a shorthand for the above lambda functions.

As per the typing rules given in Typing rules (with ρ), these functions have the following types:

\frac{\begin{gathered}\vphantom{x}\end{gathered}}{\begin{gathered}Γ ⊢ (\textbf{Ctor}\ \kappa) : (\textbf{${\mathbf{\forall{}}}$}\ (α)\ (α\ {\mathbf{\rightarrow{}}}\ {\mathbf{\ifmathjax{\unicode{x2772}}\iflatex{❲}}}(\textbf{Ctor}\ \kappa\ α) \;{\mathbf{;}}\; ϵ {\mathbf{{/}}} ⊥ \;{\mathbf{;}}\; \emptyset{}{\mathbf{\ifmathjax{\unicode{x2773}}\iflatex{❳}}}))\end{gathered}}\ {\rm T\text{-}S{\small H}{\small O}{\small R}{\small T}{\small H}{\small A}{\small N}{\small D}\text{-}C{\small T}{\small O}{\small R}}

[Write their types here too.]Todo

The polymorphic builder function for a record which intuitively corresponds to (\textbf{record}\ \overrightarrow{a}) can be written as the η-expansion of the (\textbf{record}\ \overrightarrow{a = e}) operator:

\mathbf{\Lambda{}}(\overrightarrow{α{}_i}).\mathbf{λ}(\overrightarrow{x{}_i : α{}_i}).(\textbf{record}\ \overrightarrow{a{}_i = x{}_i})

The same applies to the predicate forms of record types:

\begin{gathered} \mathbf{λ}(x : ⊤).\mathbf{(}(\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i})\ x\mathbf{)} \\ \mathbf{λ}(x : ⊤).\mathbf{(}(\textbf{record$\mathbf{*}$?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j})\ x\mathbf{)} \end{gathered}

The same applies to the accessor for a field of a record:

\mathbf{\Lambda{}}(α).(\textbf{$\Lambda{}$${}_{\textbf{f}}$}\ (\varrho{}_{f})\ \mathbf{λ}(x : (\textbf{record}\ \varrho{}_{f}\ +a:τ)).x.a)

[Write their types here too.]Todo

As a convenience, we will write (\textbf{record}\ \overrightarrow{a}), (\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}), (\textbf{record?}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{a{}_i}\ \def\overrightbracedarrow#1{\overset{\scriptscriptstyle{\raise1mu{\{}}}{\vphantom{#1}}\overrightarrow{#1}\overset{\scriptscriptstyle{\raise1mu{\}}}}{\vphantom{#1}}}\overrightbracedarrow{-a{}_j}) and .a as shorthands for the above lambda functions.

6 Typed nanopass

6.1 Typed nanopass on trees

6.2 Typed nanopass on DAGs

6.3 Typed nanopass on graphs

6.4 Structural invariants

6.5 Further possible extensions

7 Examples and results

8 Conclusion and future work directions

9 Bibliography

Harold Abelson, R Kent Dybvig, Christopher T Haynes, Guillermo Juan Rozas, NI Adams, Daniel P Friedman, E Kohlbecker, GL Steele, David H Bartley, Robert Halstead, and others. Revised 5 report on the algorithmic language Scheme. Higher-order and symbolic computation 11(1), pp. 7–105, 1998.

Michael D Adams and R Kent Dybvig. Efficient nondestructive equality checking for trees and graphs. In Proc. ACM Sigplan Notices, 2008.

Chris Andreae, James Noble, Shane Markstrum, and Todd Millstein. A framework for implementing pluggable type systems. In Proc. ACM SIGPLAN Notices, 2006.

Daniel G. Bobrow, Linda G. DeMichiel, Richard P. Gabriel, Sonya E. Keene, Gregor Kiczales, and David A. Moon. Common lisp object system specification. ACM Sigplan Notices 23(SI), pp. 1–142, 1988. http://dl.acm.org/citation.cfm?id=885632

Ambrose Bonnaire-Sergeant, Rowan Davies, and Sam Tobin-Hochstadt. Practical optional types for Clojure. In Proc. European Symposiumon ProgrammingLanguagesand Systems, 2016. http://link.springer.com/chapter/10.1007/978-3-662-49498-1_4

Gilad Bracha. Pluggable Type Systems. In Proc. OOPSLA workshop on revival of dynamic languages, 2004.

Luca Cardelli and Peter Wegner. On understanding types, data abstraction, and polymorphism. ACM Computing Surveys (CSUR) 17(4), pp. 471–523, 1985. http://lucacardelli.name/papers/onunderstanding.a4.pdf

Stephen Chang, Alex Knauth, and Ben Greenman. Type systems as macros. In Proc. Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, 2017.

Roland Ducournau. Programmation par Objets: les concepts fondamentaux. Université de Montpellier, 2014.

Jean-Baptiste Evain and others. Mono.Cecil library. 2008.

Matthias Felleisen, Robert Bruce Findler, Matthew Flatt, Shriram Krishnamurthi, Eli Barzilay, Jay McCarthy, and Sam Tobin-Hochstadt. The racket manifesto. In Proc. LIPIcs-Leibniz International Proceedings in Informatics, 2015.

Matthew Flatt. Binding as sets of scopes. ACM SIGPLAN Notices 51(1), pp. 705–717, 2016.

Matthew Flatt, Robert Bruce Findler, and Matthias Felleisen. Scheme with classes, mixins, and traits. In Proc. Asian Symposiumon ProgrammingLanguagesand Systems, 2006. http://link.springer.com/chapter/10.1007/11924661_17

Steven E Ganz, Amr Sabry, and Walid Taha. Macros as multi-stage computations: type-safe, generative, binding macros in MacroML. ACM SIGPLAN Notices 36(10), pp. 74–85, 2001.

Roger Hindley. The principal type-scheme of an object in combinatory logic. Transactions of the american mathematical society 146, pp. 29–60, 1969.

Gérard Huet. The Zipper. Journal of Functional Programming 7(5), pp. 549–554, 1997.

Andrew M Kent, David Kempe, and Sam Tobin-Hochstadt. Occurrence typing modulo theories. In Proc. ACM SIGPLAN Notices, 2016.

Alexander Köplinger, Jean-Baptiste Evain, and others. Mono.Cecil documentation. 2014.

John McCarthy. History of Programming Languages I. 1981.

Robin Milner. A theory of type polymorphism in programming. Journal of computer and system sciences 17(3), pp. 348–375, 1978.

Yaron Minsky, Anil Madhavapeddy, and Jason Hickey. Real World OCaml: Functional programming for the masses. 2013a.

Yaron Minsky, Anil Madhavapeddy, and Jason Hickey. Real World OCaml: functional programming for the masses. 2013b.

James H Morris. Real programming in functional languages. Functional Programming and Its Applications: An Advanced Course, pp. 129–176, 1982.

Henrik Nilsson and Peter Fritzson. Lazy algorithmic debugging: Ideas for practical implementation. In Proc. International Workshop on Automated and Algorithmic Debugging, 1993.

Jeffrey Overbey. Immutable Source-Mapped Abstract Syntax Tree: A Design Pattern for Refactoring Engine APIs. 2013.

Zachary Palmer, Pottayil Harisanker Menon, Alexander Rozenshteyn, and Scott Smith. Types for FlexibleObjects. In Proc. Programming Languagesand Systems, 2014. http://link.springer.com/chapter/10.1007/978-3-319-12736-1_6

Norman Ramsey and João Dias. An ApplicativeControl-FlowGraphBasedon Huet’s Zipper. Electronic Notes in Theoretical Computer Science 148(2), pp. 105–126, 2006. http://www.sciencedirect.com/science/article/pii/S1571066106001289

D. W. Sandberg. Smalltalk and Exploratory Programming. SIGPLAN Notices 23(10), pp. 85–92, 1988.

Alex Shinn, JOHN Cowan, Arthur A Gleckler, and others. Revised 7 report on the algorithmic language scheme. , 2013.

Michael Sperber, R Kent Dybvig, Matthew Flatt, Anton Van Straaten, Robby Findler, and Jacob Matthews. Revised 6 report on the algorithmic language Scheme. Journal of Functional Programming 19(S1), pp. 1–301, 2009.

Sam Tobin-Hochstadt. Typed scheme: Fromscripts to programs. 2010.

Sam Tobin-Hochstadt and Matthias Felleisen. The design and implementation of typed scheme. ACM SIGPLAN Notices 43(1), pp. 395–406, 2008. http://dl.acm.org/citation.cfm?id=1328486

Sam Tobin-Hochstadt, Vincent St-Amour, Ryan Culpepper, Matthew Flatt, and Matthias Felleisen. Languages as libraries. In Proc. ACMSIGPLANNotices, 2011. http://dl.acm.org/citation.cfm?id=1993514

Emina Torlak and Rastislav Bodik. Growing solver-aided languages with Rosette. In Proc. Proceedings of the 2013 ACMinternational symposium on Newideas, new paradigms, and reflections on programming & software, 2013. http://dl.acm.org/citation.cfm?id=2509586

Emina Torlak and Rastislav Bodik. A Lightweight Symbolic Virtual Machine for Solver-aided Host Languages. In Proc. Proceedings of the 35th ACM SIGPLAN Conference on Programming Language Design and Implementation, 2014.

Philip Wadler. Functional Programming. SIGPLAN Notices 33(8), pp. 23–27, 1998.

A Ph.C Graph library: Implementation

Georges Dupéron <georges.duperon@gmail.com>

This library is implemented using literate programming. The implementation details are presented in the following sections. The user documentation is in the Ph.C Graph library document.

A.1 Parametric replacement of parts of data structures

A.1.1 Introduction

A.1.2 Implementation

A.1.2.1 Caching the results of define-fold

A.1.3 Putting it all together

A.2 Flexible functional modification and extension of records

A.2.1 Goals

A.2.2 Overview

A.2.3 Generating the tree type with polymorphic holes

A.2.4 From a selection of field indieces to a tree shape

A.2.5 Empty branches (branches only containing missing fields)

A.2.6 Creating a record builder given a set of field indices

A.2.7 Row typing

A.2.7.1 Type of a record, with a multiple fields

A.2.8 Type of a record, with a single hole

A.2.9 Functionally updating a tree-record

A.2.9.1 Adding and modifying fields

A.2.10 Auxiliary values

A.2.11 Type of a tree-record

A.2.12 Conversion to and from record-trees

A.2.12.1 Creating a new tree-record

A.2.12.2 Extracting all the fields from a tree-record

A.2.13 Defining the converters and accessors for each known record type

A.2.13.1 Putting it all together

A.2.14 Utility math functions for binary tree manipulation

A.3 Tracking checked contracts via refinement types

A.3.1 Introduction

A.3.2 Implementation overview : subtyping, variance and phantom types

A.3.3 Encoding property implication as subtyping

A.3.3.1 Properties applying to all reachable nodes from x

A.3.3.2 Prefix trees to the rescue

A.3.3.3 Cycles in properties

A.3.3.4 Partial paths

A.3.3.5 Array and list indices

A.3.3.6 Other richer properties

A.3.4 Implementation

A.3.4.1 The witness value

A.3.4.2 Grouping multiple invariants

A.3.4.3 Structural (in)equality and (non-)membership invariants

A.3.4.3.1 Invariants and their relationships

A.3.4.4 Parsing paths

A.3.4.4.1 Comparison operator tokens

A.3.4.5 Putting it all together

A.4 Compile-time graph metadata

A.4.1 Graph type information

A.4.2 Graph builder information

A.4.3 Node information

A.4.4 Field information

A.4.5 Invariant information

A.4.6 Dependent invariant information

A.4.7 Mapping information

A.4.8 Printing

A.5 Declaring graph types

A.5.1 Implementation

A.5.2 Declaring the node types

A.5.3 Creating the graph-info instance

A.5.4 Putting it all together

A.6 Implementation of the graph macro

A.6.1 Overview of the implementation (draft)

A.7 Draft of the implementation of the graph macro

A.8 Generalised constructor functions for flexible structures

A.1 Parametric replacement of parts of data structures

A.1.1 Introduction

A.1.2 Implementation

A.1.2.1 Caching the results of define-fold

A.1.3 Putting it all together

A.1.1 Introduction

This utility allows functionally updating parts of data structures. The define-fold macro takes the type of the whole data structure and a list of type names associated with their predicate. It locates all literal occurrences of those type names within the data structure, and identifies those locations as the parts to replace. The type of the whole data structure is expressed as a syntactic tree. Within that syntactic tree, only the parts which are syntactically equal to one of the types to replace are considered.

As an example, suppose the whole type is (List Foo Number (Listof String)), and Foo is defined as:

(define-type Foo (Listof String))

If Foo is given as a type to replace, and its replacement type is (Listof Symbol), then the type of the result would be:

(List (Listof Symbol) Number (Listof String))

The second occurrence of (Listof String), although semantically equivalent to the type to replace, Foo, will not be altered, as it is not expressed syntactically using the Foo identifier.

syntax
(define-fold function-name type-name whole-type type-to-replaceᵢ ...)

The define-fold macro takes the type of the whole data structure, and a list of types to replace, each associated with a predicate for that type. It defines (type-name Tᵢ ...) as a polymorphic type, with one type argument for each type-to-replaceᵢ, such that

(type-name type-to-replaceᵢ ...)

is the same type as

whole-type

In other words, type-name is defined as whole-type, except that each syntactic occurrence of a type-to-replaceᵢ is replaced with the corresponding type argument Tᵢ.

It also defines function-name as a function, with the type

(∀ (Aᵢ ... Bᵢ ... Acc)
   (→ (?@ (→ Any Boolean : Aᵢ)
          (→ Aᵢ Acc (Values Bᵢ Acc)))
      ...
      (→ (type-name Aᵢ ...)
         Acc
         (Values (type-name Bᵢ ...)
                 Acc))))

We use the ?@ notation from syntax/parse/experimental/template to indicate that the function accepts a predicate, followed by an update function, followed by another predicate, and so on. For example, the function type when there are three type-to-replaceᵢ would be:

(∀ (A₁ A₂ A₃ B₁ B₂ B₃ Acc)
   (→ (→ Any Boolean : A₁)
      (→ A₁ Acc (Values B₁ Acc))
      (→ Any Boolean : A₂)
      (→ A₂ Acc (Values B₂ Acc))
      (→ Any Boolean : A₃)
      (→ A₃ Acc (Values B₃ Acc))
      (→ (type-name A₁ A₂ A₃)
         Acc
         (Values (type-name B₁ B₂ B₃)
                 Acc))))

The function-name replaces all values in the whole data structure which are present in locations corresponding to a type-to-replaceᵢ in the whole-type. It expects those values to have the type Aᵢ, i.e. its input type is not restricted to whole-type, any polymorphic instance of type-name is valid. Each value is passed as an argument to the corresponding update function with type (→ Aᵢ Acc (Values Bᵢ Acc)), and the result of type Bᵢ is used as a replacement.

An accumulator value, with the type Acc, is threaded through all calls to all update functions, so that the update functions can communicate state in a functional way.

A.1.2 Implementation

A.1.2.1 Caching the results of define-fold

«with-folds» ::=

(define-for-syntax get-f-cache (make-parameter #f))
(define-for-syntax get-τ-cache (make-parameter #f))
(define-for-syntax get-f-defs (make-parameter #f))
(define-for-syntax get-τ-defs (make-parameter #f))
(define-for-syntax (with-folds thunk)
  ;; TODO: should probably use bound-id instead.
  (parameterize ([get-f-cache (make-mutable-free-id-tree-table)]
                 [get-τ-cache (make-mutable-free-id-tree-table)]
                 [get-f-defs (box '())]
                 [get-τ-defs (box '())])
    (define/with-syntax thunk-result (thunk))
    (with-syntax ([([f-id f-body f-type] …) (unbox (get-f-defs))]
                  [([τ-id . τ-body] …) (unbox (get-τ-defs))])
      #`(begin (define-type τ-id τ-body) …
               (: f-id f-type) …
               (define f-id f-body) …
               thunk-result))))

«api»1 ::=

(define-template-metafunction (!replace-in-type stx)
  (syntax-case stx ()
    [(_ whole-type [type-to-replaceᵢ Tᵢ] …)
     #`(#,(syntax-local-template-metafunction-introduce
           (fold-τ #'(whole-type type-to-replaceᵢ …))) Tᵢ …)]))

«api»2 ::=

(define-template-metafunction (!∀-replace-in-type stx)
  (syntax-case stx ()
    [(_ whole-type type-to-replaceᵢ …)
     (syntax-local-template-metafunction-introduce
      (fold-τ #'(whole-type type-to-replaceᵢ …)))]))

«fold-τ» ::=

(define fold-τ
  (syntax-parser
    [(whole-type:type type-to-replaceᵢ:type …)
     #:with rec-args #'([type-to-replaceᵢ Tᵢ] …)
     (cached [τ-
              (get-τ-cache)
              (get-τ-defs)
              #'(whole-type type-to-replaceᵢ …)]
             (define replacements
               (make-immutable-free-id-tree-table
                (list [cons #'type-to-replaceᵢ #'Tᵢ] …)))
             #`(∀ (Tᵢ …)
                  #,(syntax-parse #'whole-type
                      #:literals (Null Pairof Listof List Vectorof Vector
                                       U tagged)
                      «type-cases»)))]))

«cached» ::=

(begin-for-syntax
  (define-syntax-rule (cached [base cache defs key] . body)
    (begin
      (unless (and cache defs)
        (error "fold-τ and fold-f must be called within with-folds"))
      (if (dict-has-key? cache key)
          (dict-ref cache key)
          (let ([base #`#,(gensym 'base)])
            (dict-set! cache key base)
            (let ([result (let () . body)])
              (set-box! defs `([,base . ,result] . ,(unbox defs)))
              base))))))

«api»3 ::=

(define-template-metafunction (!replace-in-instance stx)
  (syntax-case stx ()
    [(_ whole-type [type-to-replaceᵢ predicateᵢ updateᵢ] …)
     #`(#,(syntax-local-template-metafunction-introduce
           (fold-f #'(whole-type type-to-replaceᵢ …)))
        {?@ predicateᵢ updateᵢ} …)]))

«api»4 ::=

(define-template-metafunction (!λ-replace-in-instance stx)
  (syntax-case stx ()
    [(_ whole-type type-to-replaceᵢ …)
     (syntax-local-introduce
      (fold-f #'(whole-type type-to-replaceᵢ …)))]))

«fold-f» ::=

(define fold-f
  (syntax-parser
    [(whole-type:type type-to-replaceᵢ:type …)
     #:with rec-args #'([type-to-replaceᵢ predicateᵢ updateᵢ] …)
     (define replacements
       (make-immutable-free-id-tree-table
        (list [cons #'type-to-replaceᵢ #'updateᵢ] …)))
     (define/with-syntax args #'({?@ predicateᵢ updateᵢ} …))
     (cached [f-
              (get-f-cache)
              (get-f-defs)
              #'(whole-type type-to-replaceᵢ …)]
             #`[«fold-f-proc»
                «fold-f-type»])]))

«fold-f-proc» ::=

(λ ({?@ predicateᵢ updateᵢ} …)
  (λ (v acc)
    #,(syntax-parse #'whole-type
        #:literals (Null Pairof Listof List
                         Vectorof Vector U tagged)
        «f-cases»)))

«fold-f-type» ::=

(∀ (Aᵢ … Bᵢ … Acc)
   (→ (?@ (→ Any Boolean : Aᵢ)
          (→ Aᵢ Acc (Values Bᵢ Acc)))
      …
      (→ (!replace-in-type whole-type [type-to-replaceᵢ Aᵢ] …)
         Acc
         (Values (!replace-in-type whole-type [type-to-replaceᵢ Bᵢ] …)
                 Acc))))

«f-cases»1 ::=

[t
#:when (dict-has-key? replacements #'t)
#:with update (dict-ref replacements #'t)
#'(update v acc)]

«type-cases»1 ::=

[t
#:when (dict-has-key? replacements #'t)
#:with T (dict-ref replacements #'t)
#'T]

«type-cases»2 ::=

[(~or Null (List))
#'Null]

«f-cases»2 ::=

[(~or Null (List))
#'(values v acc)]

«type-cases»3 ::=

[(Pairof X Y)
#'(Pairof (!replace-in-type X . rec-args)
(!replace-in-type Y . rec-args))]

«f-cases»3 ::=

[(Pairof X Y)
#'(let*-values ([(result-x acc-x)
                  ((!replace-in-instance X . rec-args) (car v) acc)]
                 [(result-y acc-y)
                  ((!replace-in-instance Y . rec-args) (cdr v) acc-x)])
     (values (cons result-x result-y) acc-y))]

«type-cases»4 ::=

[(Listof X)
#'(Listof (!replace-in-type X . rec-args))]

«f-cases»4 ::=

[(Listof X)
#'(foldl-map (!replace-in-instance X . rec-args)
acc v)]

«type-cases»5 ::=

[(Vectorof X)
#'(Vectorof (!replace-in-type X . rec-args))]

«ftype-cases» ::=

[(Vectorof X)
#'(vector->immutable-vector
    (list->vector
     (foldl-map (!replace-in-instance X . rec-args)
                acc
                (vector->list v))))]

«type-cases»6 ::=

[(List X Y …)
#'(Pairof (!replace-in-type X . rec-args)
(!replace-in-type (List Y …) . rec-args))]

«f-cases»5 ::=

[(List X Y …)
#'(let*-values ([(result-x acc-x) «f-list-car»]
[(result-y* acc-y*) «f-list-cdr»])
(values (cons result-x result-y*) acc-y*))]

where the replacement is applied to the car, and to the cdr as a whole (i.e. by recursion on the whole remaining list of types):

«f-list-car» ::=

((!replace-in-instance X . rec-args) (car v) acc)

«f-list-cdr» ::=

((!replace-in-instance (List Y …) . rec-args) (cdr v) acc-x)

«type-cases»7 ::=

[(U Xⱼ …)
#'(U (!replace-in-type Xⱼ . rec-args) …)]

«f-cases»6 ::=

[(U Xⱼ …)
#'(dispatch-union v
                   ([type-to-replaceᵢ Aᵢ predicateᵢ] …)
                   [Xⱼ ((!replace-in-instance Xⱼ . rec-args) v acc)]
                   …)]

«type-cases»8 ::=

[(tagged name [fieldⱼ (~optional :colon) Xⱼ] …)
#'(tagged name [fieldⱼ : (!replace-in-type Xⱼ . rec-args)] …)]

«f-cases»7 ::=

[(tagged name [fieldⱼ (~optional :colon) Xⱼ] …)
#'(let*-values
       ([(resultⱼ acc)
         ((!replace-in-instance Xⱼ . rec-args) (uniform-get v fieldⱼ)
                                               acc)]
        …)
     (values (tagged name #:instance [fieldⱼ resultⱼ] …)
             acc))]

«type-cases»9 ::=

[else-T
#'else-T]

«f-cases»8 ::=

[else-T
#'(values v acc)]

where foldl-map is defined as:

«foldl-map» ::=

(: foldl-map (∀ (A B Acc) (→ (→ A Acc (Values B Acc))
                             Acc
                             (Listof A)
                             (Values (Listof B) Acc))))
(define (foldl-map f acc l)
  (if (null? l)
      (values l
              acc)
      (let*-values ([(v a) (f (car l) acc)]
                    [(ll aa) (foldl-map f a (cdr l))])
        (values (cons v ll)
                aa))))

A.1.3 Putting it all together

«*» ::=

(require racket/require
         phc-toolkit
         type-expander
         phc-adt
         "dispatch-union.rkt"
         (for-syntax  (subtract-in racket/base
                                   subtemplate/override)
                      subtemplate/override
                      phc-toolkit/untyped
                      type-expander/expander
                      "free-identifier-tree-equal.rkt"
                      racket/dict)
         (for-meta 2 racket/base)
         (for-meta 2 phc-toolkit/untyped)
         (for-meta 2 syntax/parse))

(provide (for-syntax with-folds
                     !replace-in-type
                     !∀-replace-in-type
                     !replace-in-instance
                     !λ-replace-in-instance))
«foldl-map»
«with-folds»
«cached»
(begin-for-syntax
  «api»
  «fold-τ»
  «fold-f»)

A.2 Flexible functional modification and extension of records

A.2.1 Goals

Our goal here is to have strongly typed records, with row polymorphism (a Rest row type variable can range over multiple possibly-present fields), and structural type equivalence (two record types are identical if they have the same fields and the type of the fields is the same in both record types).

A.2.2 Overview

We represent a flexible record as a tree, where the leaves are field values. Every field which occurs anywhere in the program is assigned a constant index. This index determines which leaf is used to store that field’s values. In order to avoid storing in-memory a huge tree for every record, the actual fields are captured by a closure, and the tree is lazily generated (node by node) upon access.

The type for a flexible record can support row polymorphism: the type of fields which may optionally be present are represented by a polymorphic type variable. Note that this means that not only one type variable is used, but severalIn principle, each potentially-present field would need a distinct type variable, but whole potentially-present branches may be collapsed to a single type variable if no access is made to the variables within..

A.2.3 Generating the tree type with polymorphic holes

We define in this section facilities to automatically generate this list of polymorphic type variables. In order to avoid having a huge number of type variables, a branch containing only optional fields can be collapsed into a single type variable. An exception to this rule is when a field needs to be added or modified by the user code: in this case the polymorphic type variable for that field must be preserved, and the branch may not entirely be collapsed.

We take as an example the case where that there are 8 fields (f1, f2, a, b, f5, f6, f7 and u) used in the whole program. Records are therefore represented as a tree of depth 4 (including the root node) with 8 leaves. A record with the fields a and b will be represented as a tree where the branch containing f1 and f2 is collapsed. Furthermore, the right branch of the root, containing f5, f6, f7 and u will also be collapsed.

Figure 1: The tree representing the type for a record with fields a and b is ((C¹. (a . b)) . C²), where Cⁱ indicates that a single polymorphic type is used to represent the type of the whole collapsed branch.

Figure 3: Updating the node u, which appears somewhere in the collapsed branch C² is not possible, because the type abstracted away by C² may be different before and after the update.

Figure 3: We therefore break apart the collapsed branch C². The tree representing the type for a record with fields a and b, and where the field u may be updated or added, is ((C¹. (a . b)). (C²′. (C³ . u))). Note that u may refer to a possibly absent field (in which case the polymorphic type variable will be instantiated with None.

A.2.4 From a selection of field indieces to a tree shape

phase 1 procedure
(idx→tree none-wrapper
leaf-wrapper
node-wrapper
vec) → r
   none-wrapper :
(->d [depth exact-nonnegative-integer?]
     any/c)
   leaf-wrapper :
(->d [i-in-vec exact-nonnegative-integer?]
     [leaf-idx exact-nonnegative-integer?]
     any/c)
   node-wrapper :
(->d [left any/c]
     [right any/c]
     any/c)
  vec : (vectorof exact-nonnegative-integer?)

Given a flat list of field indicies (that is, leaf positions in the tree representation), idx→tree generates tree-shaped code, transforming each leaf with leaf-wrapper, each intermediate node with node-wrapper and each leaf not present in the initial list with none-wrapper.

«idx→tree» ::=

(define/contract (idx→tree #:none-wrapper none-wrapper
                           #:leaf-wrapper leaf-wrapper
                           #:node-wrapper node-wrapper
                           #:vec vec)
  «idx→tree/ctc»
  (define (r #:depth depth
             #:vec-bounds vec-start vec-after-end
             #:leaf-bounds first-leaf after-last-leaf)
    (cond
      «idx→tree cases»))
  r)

«idx→tree/ctc»1 ::= expand

;; contract for idx→tree, as specified above

«idx→tree/ctc»2 ::= collapse

;; contract for idx→tree, as specified above
(-> #:none-wrapper (->d ([depth exact-nonnegative-integer?])
                        [result any/c])
    #:leaf-wrapper (->d ([i-in-vec exact-nonnegative-integer?]
                         [leaf-idx exact-nonnegative-integer?])
                        any)
    #:node-wrapper (->d ([left any/c]
                         [right any/c])
                        any)
    #:vec (vectorof exact-nonnegative-integer?)
    (-> #:depth exact-nonnegative-integer?
        #:vec-bounds exact-nonnegative-integer?
                     exact-nonnegative-integer?
        #:leaf-bounds exact-nonnegative-integer?
                      exact-nonnegative-integer?
        any/c))

The idx→tree is a two-step curried function, and the first step returns a function with the following signature:

procedure
(r #:depth depth
#:vec-bounds vec-start
vec-after-end
#:leaf-bounds first-leaf
after-last-leaf) → any/c
  depth : exact-nonnegative-integer?
  vec-start : exact-nonnegative-integer?
  vec-after-end : exact-nonnegative-integer?
  first-leaf : exact-nonnegative-integer?
  after-last-leaf : exact-nonnegative-integer?

The idx→tree function works by performing repeated dichotomy on the vector of present fields vec.

«idx→tree cases»1 ::=

(cond
  [(= vec-start vec-after-end)
   (none-wrapper depth)]
  [(= (+ first-leaf 1) after-last-leaf)
   (leaf-wrapper vec-start (vector-ref vec vec-start))]
  [else
   (let* ([leftmost-right-leaf (/ (+ first-leaf after-last-leaf) 2)]
          [vec-left-branch-start vec-start]
          [vec-left-branch-after-end
           (find-≥ leftmost-right-leaf vec vec-start vec-after-end)]
          [vec-right-branch-start vec-left-branch-after-end]
          [vec-right-branch-after-end vec-after-end])
     (node-wrapper
      (r #:depth (sub1 depth)
         #:vec-bounds vec-left-branch-start
                      vec-left-branch-after-end
         #:leaf-bounds first-leaf
                       leftmost-right-leaf)
      (r #:depth (sub1 depth)
         #:vec-bounds vec-right-branch-start
                      vec-right-branch-after-end
         #:leaf-bounds leftmost-right-leaf
                       after-last-leaf)))])

The find-≥ function performs the actual dichotomy, and finds the first index within the given bounds for which (vector-ref vec result) is greater than or equal to val (if there is none, then the upper exclusive bound is returned).

«dichotomy» ::=

(define/contract (find-≥ val vec start end)
  (->i ([val exact-nonnegative-integer?]
        [vec vector?] ;; (sorted-vectorof exact-nonnegative-integer? <)
        [start (vec) (integer-in 0 (sub1 (vector-length vec)))]
        [end (vec start) (integer-in (add1 start) (vector-length vec))])
       #:pre (val vec start) (or (= start 0)
                                 (< (vector-ref vec (sub1 start)) val))
       #:pre (val vec end) (or (= end (vector-length vec))
                               (> (vector-ref vec end) val))
       [result (start end) (integer-in start end)])
  (if (= (- end start) 1) ;; there is only one element
      (if (>= (vector-ref vec start) val)
          start
          end)
      (let ()
        (define mid (ceiling (/ (+ start end) 2)))
        (if (>= (vector-ref vec mid) val)
            (find-≥ val vec start mid)
            (find-≥ val vec mid end)))))

A.2.5 Empty branches (branches only containing missing fields)

For efficiency and to reduce memory overhead, we pre-define values for branches of depth d ∈ (range 0 n) which only contain missing fields.

«empty-branches» ::=

;; TODO: clean this up (use subtemplate).
(define-syntax defempty
  (syntax-parser
    [(_ n:nat)
     #:with (empty1 emptyA …)
     (map (λ (depth)
            (string->symbol (format "empty~a" (expt 2 depth))))
          (range (add1 (syntax-e #'n))))
     #:with (emptyB … _) #'(empty1 emptyA …)
     #:with (empty1/τ emptyA/τ …) (stx-map λ.(format-id % "~a/τ" %)
                                           #'(empty1 emptyA …))
     #:with (emptyB/τ … _) #'(empty1/τ emptyA/τ …)
     (syntax-local-introduce
      #'(begin (define-type empty1/τ 'none)
               (define-type emptyA/τ (Pairof emptyB/τ emptyB/τ))
               …
               (define empty1 : empty1/τ 'none)
               (define emptyA : emptyA/τ (cons emptyB emptyB))
               …
               (provide empty1 emptyA …
                        empty1/τ emptyA/τ …)))]))
(defempty 10)

A.2.6 Creating a record builder given a set of field indices

«record-builder» ::=

(define-syntax record-builder
  (syntax-parser
    ;; depth ≥ 0. 0 ⇒ a single node, 1 ⇒ 2 nodes, 2 ⇒ 4 nodes and so on.
    [(_ depth:nat idx:nat …)
     #:when (not (check-duplicates (syntax->datum #'(idx …))))
     (define vec (list->vector (sort (syntax->datum #'(idx …)) <)))
     (define arg-vec (vector-map (λ (idx)
                                   (format-id               (syntax-local-introduce #'here)
                                              "arg~a"
                                              idx))
                                 vec))
     (define/with-syntax #(arg …) arg-vec)

     (define/with-syntax tree
       ((idx→tree «record-builder/wrappers»
                  #:vec vec)
        #:depth (syntax-e #'depth)
        #:vec-bounds 0 (vector-length vec)
        #:leaf-bounds 0 (expt 2 (syntax-e #'depth))))
     (define/with-syntax (arg/τ …) (stx-map (λ (arg)
                                              (format-id arg "~a/τ" arg))
                                            #'(arg …)))
     #'(λ #:∀ (arg/τ …) ([arg : arg/τ] …)
         tree)]))

«record-builder/wrappers»1 ::=

(idx→tree
#:none-wrapper λdepth.(format-id #'here "empty~a" (expt 2 depth))
#:leaf-wrapper λi.idx.(vector-ref arg-vec i)
#:node-wrapper λl.r.(list #'cons l r)
#:vec vec)

A.2.7 Row typing

Row type variable identifiers are bound as transformers to instances of the ρ-wrapper struct, so that they are easily recognisable by special forms such as record.

«ρ-wrapper»1 ::= expand

(begin-for-syntax
(struct ρ-wrapper (id)))

«ρ-wrapper»2 ::= collapse

(begin-for-syntax
  (struct ρ-wrapper (id)
    #:property prop:procedure
    (λ (self stx)
      (raise-syntax-error (syntax-e (ρ-wrapper-id self))
                          "invalid use of row type variable"
                          stx))))

The row type variable actually expands to several polymorphic type variables. In order to know which fields are relevant, we remember which fields are used along a given row type variable, while compiling the current file. The set of field names used with a given row types variable is stored as an entry of the ρ-table.

«ρ-table» ::=

(define-for-syntax ρ-table (make-free-id-table))

A record type which includes a row type variable is expanded to the type of a binary tree. Fields which are used along that row type variable matter, and must be explicitly indicated as optional leaves (so that operations which add or remove fields later in the body of a row-polymorphic function may refer to that leaf). Branches which only contain irrelevant leaves can be collapsed to a single polymorphic type. The core implementation of record types (in which the depth of the tree is explicitly given, and ) follows. Since the code is very similar to the defintion of idx→tree, the unchanged parts are dimmed below.

«record-type»1 ::=

(define-type-expander record-type
  (syntax-parser
    [(_ depth:nat idx:nat …)
     #:when (not (check-duplicates (syntax->datum #'(idx …))))
     (define vec (list->vector (sort (syntax->datum #'(idx …)) <)))
     (define arg-vec (vector-map (λ (idx)
                                   (format-id               (syntax-local-introduce #'here)
                                              "arg~a"
                                              idx))
                                 vec))
     (define/with-syntax #(arg …) arg-vec)

     (define/with-syntax tree
       ((idx→tree «record-type/wrappers»
                  #:vec vec)
        #:depth (syntax-e #'depth)
        #:vec-bounds 0 (vector-length vec)
        #:leaf-bounds 0 (expt 2 (syntax-e #'depth))))
     (define sidekicks-len 0)
     (define sidekicks '())
     #`(∀ (arg … #,@sidekicks) tree)]))

The results of record-type and record-builder differ in two aspects: the result of record-type is a polymorphic type, not a function, and the empty branches are handled differently. When a branch only containing none elements is encountered, it is replaced with a single polymorphic type.

«record-type/wrappers»1 ::=

(idx→tree
#:none-wrapper λdepth.(begin
                         (define sidekick (format-id #'here "row~a" sidekicks-len))
                         (set! sidekicks-len (add1 sidekicks-len))
                         (set! sidekicks (cons sidekick sidekicks))
                         sidekick)
#:leaf-wrapper λi.idx.(vector-ref arg-vec i)
#:node-wrapper λl.r.(list #'Pairof l r)
#:vec vec)

Since the list of fields may be amended long after the type was initially expanded, we delay the expansion of the type. This is done by initially expanding to a placeholder type name, and later patching the expanded code to replace that placeholder with the actual expanded record type. current-patch-table maps each placeholder to an anonymous function which will produce the syntax for the desired type when called.

«current-patch-table» ::=

(define-for-syntax current-patch-table (make-parameter #f))

Type-level forms like ∀ρ, ρ-inst and record add placeholders to current-patch-table.

The form with-ρ is used to declare row type variables and collect patches in current-patch-table. The explicit declaration of row type variables is necessary because type variables which are logically “bound” with ∀ are not actually bound as identifiers during macro expansion (instead, Typed Racket performs its own resolution while typechecking, i.e. after the program is expanded). If a row type variable is introduced in the type declaration for a function, we need to be able to detect the binding when processing type-level forms within the body of the function.

«with-ρ» ::=

(define-syntax with-ρ
  (syntax-parser
    [(_ (ρ …) . body)
     #'(splicing-letrec-syntax ([ρ (ρ-wrapper #'ρ)] …)
         (with-ρ-chain (ρ …) . body))]))

Once the bindings have been introduced via splicing-letrec-syntax, the expansion continues within the context of these identifiers, via the with-ρ-chain macro.

«with-ρ-chain» ::=

(define-syntax with-ρ-chain
  (syntax-parser
    [(_ (ρ …) . body)
     (parameterize ([current-patch-table (make-free-id-table)])
       (define expanded-form
         (local-expand #'(begin . body) 'top-level '()))
       (patch expanded-form (current-patch-table)))]))

A.2.7.1 Type of a record, with a multiple fields

The ∀ρ type-level form translates to a ∀ form. The ∀ form is expanded, so that uses of the row type variables within can be detected. The ∀ρ then expands to a placeholder delayed-type, which will be patched by the surrounding with-ρ.

«∀ρ» ::=

(define-type-expander ∀ρ
  (syntax-parser
    [(_ (A:id … #:ρ ρ:id …) τ)
     (for ([ρ (in-syntax #'(ρ …))])
       (free-id-table-set! ρ-table ρ «make-lifo-set»))
     (define expanded (expand-type #'(∀ (A …) (Let ([ρ 'NOT-IMPL-YET] …) τ))))
     (define/syntax-parse ({~literal tr:∀} (A′ …) . τ′) expanded)
     (free-id-table-set! (current-patch-table)
                         #'delayed-type
                         (λ (self) (delayed-∀ρ #'{(A′ …) (ρ …) τ′})))
     #'delayed-type]))

When the delayed-type is replaced, the type variables associated with each row type variable are injected as extra arguments to the previously-expanded polymorphic type.

«delayed-∀ρ» ::=

(define-for-syntax/case-args (delayed-∀ρ {(A′ …) (ρ …) τ′})
  (define/syntax-parse ((ρ′ …) …)
    (for/list ([ρ (in-syntax #'(ρ …))])
      (for/list ([ρ′ (sort («lifo-set→list» (free-id-table-ref ρ-table
                                                               ρ))
                           symbol<?)])
        ;; TODO: the format-id shouldn't be here, it should be when
        ;; the id is added to the list. Also #'here is probably the
        ;; wrong srcloc
        (format-id #'here "~a.~a" ρ ρ′))))
  #'(∀ (A′ … ρ′ … …) . τ′))

«record-type»3 ::=

«ρ-wrapper»
«current-patch-table»

«with-ρ-chain»
«with-ρ»

«ρ-table»
«∀ρ»

«delayed-∀ρ»

(define-type-expander record
  (syntax-parser
    [(_ f:id … . {~or (#:ρ ρ:id) ρ:id})
     (define set
       (free-id-table-ref! ρ-table #'ρ (λ () «make-lifo-set»)))
     (for ([f (in-syntax #'(f …))])
       («lifo-set-add!» set (syntax->datum f)))
     #'(List 'f … 'ρ)]))

(define-syntax ρ-inst
  (syntax-parser
    [(_ f A:id … #:ρ ρ:id …)
     #'TODO]))

«make-lifo-set» ::=

;; ordered free-identifier-set, last added = first in the order.
(cons (box '()) (mutable-set))

«lifo-member?» ::=

(λ (s v) (set-member? (cdr s) v))

«lifo-set-add!» ::=

(λ (s v)
  (unless («lifo-member?» s v)
    (set-box! (car s) (cons v (unbox (car s)))))
  (set-add! (cdr s) v))

«lifo-set→list» ::=

(λ (s) (unbox (car s)))

«patch» ::=

(define-for-syntax (patch e tbl)
  (define (patch* e)
    (cond
      ;[(syntax-case e ()
      ;   [(x y)
      ;    (free-id-table-ref tbl x (λ () #f))
      ;    (values #t ((free-id-table-ref tbl x) e))]
      ;   [_ #f])]
      [(and (identifier? e)
            (free-id-table-ref tbl e (λ () #f)))
       => (λ (f) (values #t (f e)))]
      [(syntax? e)
       (let-values ([(a b) (patch* (syntax-e e))])
         (if a
             (values a (datum->syntax e b e e))
             (values a e)))]
      [(pair? e)
       (let-values ([(a1 b1) (patch* (car e))]
                    [(a2 b2) (patch* (cdr e))])
         (if (or a1 a2)
             (values #t (cons b1 b2))
             (values #f e)))]
      ;; TODO: hash, prefab etc.
      [else
       (values #f e)]))
  (let-values ([(a b) (patch* e)])
    b))

«expand-ρ» ::=

(define-for-syntax identifier<? (∘ symbol<? syntax-e))
(define-for-syntax (sort-ids ids) (sort (syntax->list ids) identifier<?))
(define-type-expander ρ/fields
  (syntax-parser
    [(_ (important-field …) (all-field …))
     #:with (sorted-important-field …) (sort-ids #'(important-field …))
     #:with (sorted-all-field …) (sort-ids #'(all-field …))

     #'~]))

A.2.8 Type of a record, with a single hole

In order to functionally update records, the updating functions will take a tree where the type of a single leaf needs to be known. This of course means that branches that spawn off on the path from the root have to be given a polymorphic type, so that the result can have the same type for these branches as the original value to update.

«tree-type-with-replacement» ::=

(define-for-syntax (tree-type-with-replacement n last τ*)
  (define-values (next mod) (quotient/remainder n 2))
  (cond [(null? τ*) last]
        [(= mod 0)
         (tree-type-with-replacement next
                                     #`(Pairof #,last #,(car τ*))
                                     (cdr τ*))]
        [else
         (tree-type-with-replacement next
                                     #`(Pairof #,(car τ*) #,last)
                                     (cdr τ*))]))

A.2.9 Functionally updating a tree-record

A.2.9.1 Adding and modifying fields

Since we only deal with functional updates of immutable records, modifying a field does little more than discarding the old value, and injecting the new value instead into the new, updated record.

Adding a new field is done using the same exact operation: missing fields are denoted by a special value, 'NONE, while present fields are represented as instances of the polymorphic struct (Some T). Adding a new field is therefore as simple as discarding the old 'NONE marker, and replacing it with the new value, wrapped with Some. A field update would instead discard the old instance of Some, and replace it with a new one.

«make-replace-in-tree-body» ::=

(if (= i 1)
    #'(delay/pure/stateless replacement)
    (let* ([bits (to-bits i)]
           [next (from-bits (cons #t (cddr bits)))]
           [mod (cadr bits)])
      (define/with-syntax next-id (vector-ref low-names (sub1 next)))
      (if mod
          #`(replace-right (inst next-id #,@τ*-limited+T-next)
                           tree-thunk
                           replacement)
          #`(replace-left (inst next-id #,@τ*-limited+T-next)
                          tree-thunk
                          replacement))))

«define-replace-in-tree» ::=

(define-pure/stateless
  (: replace-right (∀ (A B C R) (→ (→ (Promise B) R (Promise C))
                                   (Promise (Pairof A B))
                                   R
                                   (Promise (Pairof A C)))))
  (define
    #:∀ (A B C R)
    (replace-right [next-id : (→ (Promise B) R (Promise C))]
                   [tree-thunk : (Promise (Pairof A B))]
                   [replacement : R])
    (delay/pure/stateless
     (let ([tree (force tree-thunk)])
       (let ([left-subtree (car tree)]
             [right-subtree (cdr tree)])
         (cons left-subtree
               (force (next-id (delay/pure/stateless right-subtree)
                               replacement))))))))
(define-pure/stateless
  (: replace-left (∀ (A B C R) (→ (→ (Promise A) R (Promise C))
                                  (Promise (Pairof A B))
                                  R
                                  (Promise (Pairof C B)))))
  (define
    #:∀ (A B C R)
    (replace-left [next-id : (→ (Promise A) R (Promise C))]
                  [tree-thunk : (Promise (Pairof A B))]
                  [replacement : R])
    (delay/pure/stateless
     (let ([tree (force tree-thunk)])
       (let ([left-subtree (car tree)]
             [right-subtree (cdr tree)])
         (cons (force (next-id (delay/pure/stateless left-subtree)
                               replacement))
               right-subtree))))))

(define-for-syntax (define-replace-in-tree
                     low-names names rm-names τ* i depth)
  (define/with-syntax name (vector-ref names (sub1 i)))
  (define/with-syntax rm-name (vector-ref rm-names (sub1 i)))
  (define/with-syntax low-name (vector-ref low-names (sub1 i)))
  (define/with-syntax tree-type-with-replacement-name
    (gensym 'tree-type-with-replacement))
  (define/with-syntax tree-replacement-type-name
    (gensym 'tree-replacement-type))
  (define τ*-limited (take τ* depth))
  (define τ*-limited+T-next (if (= depth 0)
                                (list #'T)
                                (append (take τ* (sub1 depth))
                                        (list #'T))))
  #`(begin
      (provide name rm-name)
      (define-type (tree-type-with-replacement-name #,@τ*-limited T)
        (Promise #,(tree-type-with-replacement i #'T τ*-limited)))

      (define-pure/stateless
        (: low-name
           (∀ (#,@τ*-limited T)
              (→ (tree-type-with-replacement-name #,@τ*-limited Any)
                 T
                 (tree-type-with-replacement-name #,@τ*-limited T))))
        (define
          #:∀ (#,@τ*-limited T)
          (low-name [tree-thunk : (tree-type-with-replacement-name
                                   #,@τ*-limited Any)]
                    [replacement : T])
          : (Promise #,(tree-type-with-replacement i #'T τ*-limited))
          #,«make-replace-in-tree-body»))

      (: name
         (∀ (#,@τ*-limited T)
            (→ (tree-type-with-replacement-name #,@τ*-limited Any)
               T
               (tree-type-with-replacement-name #,@τ*-limited
                                                (Some T)))))
      (define (name tree-thunk replacement)
        (low-name tree-thunk (Some replacement)))

      (: rm-name
         (∀ (#,@τ*-limited)
            (→ (tree-type-with-replacement-name #,@τ*-limited (Some Any))
               (tree-type-with-replacement-name #,@τ*-limited 'NONE))))
      (define (rm-name tree-thunk)
        (low-name tree-thunk 'NONE))))

A.2.10 Auxiliary values

The following sections reuse a few values which are derived from the list of fields:

«utils» ::=

(define all-fields #'(field …))
(define depth-above (ceiling-log2 (length (syntax->list #'(field …)))))
(define offset (expt 2 depth-above))
(define i*-above (range 1 (expt 2 depth-above)))
(define names (list->vector
               (append (map (λ (i) (format-id #'here "-with-~a" i))
                            i*-above)
                       (stx-map (λ (f) (format-id f "with-~a" f))
                                #'(field …)))))
(define rm-names (list->vector
                  (append (map (λ (i) (format-id #'here "-without-~a" i))
                               i*-above)
                          (stx-map (λ (f) (format-id f "without-~a" f))
                                   #'(field …)))))
(define low-names (list->vector
                   (append (map (λ (i) (format-id #'here "-u-with-~a" i))
                                i*-above)
                           (stx-map (λ (f) (format-id f "u-with-~a" f))
                                    #'(field …)))))

A.2.11 Type of a tree-record

«τ-tree-with-fields» ::=

(define-for-syntax (τ-tree-with-fields struct-fields fields)
  (define/with-syntax (struct-field …) struct-fields)
  (define/with-syntax (field …) fields)
  «utils»
  ;; Like in convert-from-struct
  (define lookup
    (make-free-id-table
     (for/list ([n (in-syntax all-fields)]
                [i (in-naturals)])
       (cons n (+ i offset)))))
  (define fields+indices
    (sort (stx-map λ.(cons % (free-id-table-ref lookup %))
                   #'(struct-field …))
          <
          #:key cdr))

  (define up (* offset 2))

  ;; Like in convert-fields, but with Pairof
  (define (f i)
    (if (and (pair? fields+indices) (= i (cdar fields+indices)))
        (begin0
          `(Some ,(caar fields+indices))
          (set! fields+indices (cdr fields+indices)))
        (if (>= (* i 2) up) ;; DEPTH
            ''NONE
            (begin
              `(Pairof ,(f (* i 2))
                       ,(f (add1 (* i 2))))))))
  (f 1))

A.2.12 Conversion to and from record-trees

«define-struct↔tree» ::=

(define-for-syntax (define-struct↔tree
                     offset all-fields τ* struct-name fields)
  (define/with-syntax (field …) fields)
  (define/with-syntax fields→tree-name
    (format-id struct-name "~a→tree" struct-name))
  (define/with-syntax tree→fields-name
    (format-id struct-name "tree→~a" struct-name))
  (define lookup
    (make-free-id-table
     (for/list ([n (in-syntax all-fields)]
                [i (in-naturals)])
       (cons n (+ i offset)))))
  (define fields+indices
    (sort (stx-map λ.(cons % (free-id-table-ref lookup %))
                   fields)
          <
          #:key cdr))
  #`(begin
      (: fields→tree-name (∀ (field …)
                             (→ field …
                                (Promise
                                 #,(τ-tree-with-fields #'(field …)
                                                       all-fields)))))
      (define (fields→tree-name field …)
        (delay/pure/stateless
         #,(convert-fields (* offset 2) fields+indices)))

      (: tree→fields-name (∀ (field …)
                             (→ (Promise
                                 #,(τ-tree-with-fields #'(field …)
                                                       all-fields))
                                (Values field …))))
      (define (tree→fields-name tree-thunk)
        (define tree (force tree-thunk))
        #,(convert-back-fields (* offset 2) fields+indices))))

A.2.12.1 Creating a new tree-record

«convert-fields» ::=

(define-for-syntax (convert-fields up fields+indices)
  (define (f i)
    (if (and (pair? fields+indices) (= i (cdar fields+indices)))
        (begin0
          `(Some ,(caar fields+indices))
          (set! fields+indices (cdr fields+indices)))
        (if (>= (* i 2) up) ;; DEPTH
            ''NONE
            `(cons ,(f (* i 2))
                   ,(f (add1 (* i 2)))))))
  (f 1))

A.2.12.2 Extracting all the fields from a tree-record

We traverse the tree in preorder, and accumulate definitions naming the interesting subparts of the trees (those where there are fields).

«convert-back-fields» ::=

(define-for-syntax (convert-back-fields up fields+indices)
  (define result '())
  (define definitions '())
  (define (f i t)
    (if (and (pair? fields+indices) (= i (cdar fields+indices)))
        (begin0
          (begin
            (set! result (cons #`(Some-v #,t) result))
            #t)
          (set! fields+indices (cdr fields+indices)))
        (if (>= (* i 2) up) ;; DEPTH
            #f
            (let* ([left-t (string->symbol
                            (format "subtree-~a" (* i 2)))]
                   [right-t (string->symbol
                             (format "subtree-~a" (add1 (* i 2))))]
                   [left (f (* i 2) left-t)]
                   [right (f (add1 (* i 2)) right-t)])
              (cond
                [(and left right)
                 (set! definitions (cons #`(define #,left-t (car #,t))
                                         definitions))
                 (set! definitions (cons #`(define #,right-t (cdr #,t))
                                         definitions))
                 #t]
                [left
                 (set! definitions (cons #`(define #,left-t (car #,t))
                                         definitions))
                 #t]
                [right
                 (set! definitions (cons #`(define #,right-t (cdr #,t))
                                         definitions))
                 #t]
                [else
                 #f])))))
  (f 1 #'tree)
  #`(begin #,@definitions (values . #,(reverse result))))

A.2.13 Defining the converters and accessors for each known record type

«define-trees» ::=

(define-for-syntax (define-trees stx)
  (syntax-case stx ()
    [(bt-fields-id (field …) [struct struct-field …] …)
     (let ()
       «utils»
       (define ∀-types (map λ.(format-id #'here "τ~a" %)
                            (range (add1 depth-above))))
       (define total-nb-functions (vector-length names))
       «define-trees-result»)]))

«bt-fields-type» ::=

(define-for-syntax (bt-fields-type fields)
  (λ (stx)
    (syntax-case stx ()
      [(_ . fs)
       #`(∀ fs (Promise #,(τ-tree-with-fields #'fs
                                              fields)))])))

«define-trees-result» ::=

#`(begin
    (define-type-expander bt-fields-id
      (bt-fields-type #'#,(syntax-local-introduce #'(field …))))
    #,@(map λ.(define-replace-in-tree low-names
                names rm-names ∀-types % (floor-log2 %))
            (range 1 (add1 total-nb-functions)))

    #,@(map λ.(define-struct↔tree
                offset all-fields ∀-types %1 %2)
            (syntax->list #'(struct …))
            (syntax->list #'([struct-field …] …))))

A.2.13.1 Putting it all together

«maybe» ::=

(struct (T) Some ([v : T]) #:transparent)
(define-type (Maybe T) (U (Some T) 'NONE))

«*» ::=

(require delay-pure
         "flexible-with-utils.hl.rkt"
         phc-toolkit/syntax-parse
         (for-syntax (rename-in racket/base [... …])
                     syntax/parse
                     syntax/stx
                     racket/syntax
                     racket/list
                     syntax/id-table
                     racket/set
                     racket/sequence
                     racket/vector
                     racket/contract
                     type-expander/expander
                     phc-toolkit/untyped/syntax-parse)
         (for-meta 2 racket/base)
         (prefix-in tr: (only-in typed/racket ∀))
         racket/splicing)

(provide (for-syntax define-trees)
         ;; For tests:
         (struct-out Some)

         ;;DEBUG:
         (for-syntax τ-tree-with-fields)
         record-builder
         ∀ρ
         with-ρ
         record)

«maybe»
«tree-type-with-replacement»
«define-replace-in-tree»
;<define-remove-in-tree>
«convert-fields»
«convert-back-fields»
«τ-tree-with-fields»
«define-struct↔tree»
«define-trees»
«bt-fields-type»
(begin-for-syntax
  «dichotomy»
  «idx→tree»)
«empty-branches»
«record-builder»
«patch»
«record-type»

A.2.14 Utility math functions for binary tree manipulation

(require (lib "phc-graph/flexible-with-utils.hl.rkt"))
	package: phc-graph

«*» ::=

(require (for-syntax racket/base))

(provide (for-syntax to-bits
                     from-bits
                     floor-log2
                     ceiling-log2))

«to-bits»
«from-bits»
«floor-log2»
«ceiling-log2»

(module* test racket/base
  (require (for-template (submod "..")))
  (require rackunit)
  «test-to-bits»
  «test-from-bits»)

procedure
(to-bits n) → (listof boolean?)
n : exact-nonnegative-integer?

«to-bits» ::=

;;      1      =>                     1
;;   2     3   =>          10                  11
;; 4   5 6   7 =>    100       101       110       111
;; 89 ab cd ef => 1000 1001 1010 1011 1100 1101 1110 1111

;;      1      =>                     ε
;;   2     3   =>          0                   1
;; 4   5 6   7 =>     00       01         10       11
;; 89 ab cd ef =>  000  001 010  011   100  101 110  111

;;      0      =>                     0
;;   1     2   =>          1                  10
;; 3   4 5   6 =>    11       100       101       110
;; 78 9a bc de => 111  1000 1001 1010 1011 1100 1101 1110

(define-for-syntax (to-bits n)
  (reverse
   (let loop ([n n])
     (if (= n 0)
         null
         (let-values ([(q r) (quotient/remainder n 2)])
           (cons (if (= r 1) #t #f) (loop q)))))))

«test-to-bits» ::=

(check-equal? (to-bits 0) '())
(check-equal? (to-bits 1) '(#t))
(check-equal? (to-bits 2) '(#t #f))
(check-equal? (to-bits 3) '(#t #t))
(check-equal? (to-bits 4) '(#t #f #f))
(check-equal? (to-bits 5) '(#f . #t . #t))
(check-equal? (to-bits 6) '(#t #t #f))
(check-equal? (to-bits 7) '(#t #t #t))
(check-equal? (to-bits 8) '(#t #f #f #f))
(check-equal? (to-bits 12) '(#t #t #f #f))
(check-equal? (to-bits 1024) '(#t #f #f #f #f #f #f #f #f #f #f))

procedure
(from-bits n) → exact-nonnegative-integer?
n : (listof boolean?)

«from-bits» ::=

(define-for-syntax (from-bits b)
  (foldl (λ (bᵢ acc)
           (+ (* acc 2) (if bᵢ 1 0)))
         0
         b))

«test-from-bits» ::=

(check-equal? (from-bits '()) 0)
(check-equal? (from-bits '(#t)) 1)
(check-equal? (from-bits '(#t #f)) 2)
(check-equal? (from-bits '(#t #t)) 3)
(check-equal? (from-bits '(#t #f #f)) 4)
(check-equal? (from-bits '(#f . #t . #t)) 5)
(check-equal? (from-bits '(#t #t #f)) 6)
(check-equal? (from-bits '(#t #t #t)) 7)
(check-equal? (from-bits '(#t #f #f #f)) 8)
(check-equal? (from-bits '(#t #t #f #f)) 12)
(check-equal? (from-bits '(#t #f #f #f #f #f #f #f #f #f #f)) 1024)

procedure
(floor-log2 n) → exact-nonnegative-integer?
n : exact-positive-integer?

Exact computation of

\lfloor\log_2(n)\rfloor.

«floor-log2» ::=

(define-for-syntax (floor-log2 n)
  (if (<= n 1)
      0
      (add1 (floor-log2 (quotient n 2)))))

procedure
(ceiling-log2 n) → exact-nonnegative-integer?
n : exact-positive-integer?

Exact computation of

\lceil\log_2(n)\rceil.

«ceiling-log2» ::=

(define-for-syntax (ceiling-log2 n)
(floor-log2 (sub1 (* n 2))))

A.3 Tracking checked contracts via refinement types

A.3.1 Introduction

The cautious compiler writer will no doubt want to check that the Abstract Syntax Tree or Graph used to represent the program verifies some structural properties. For example, the compiled language might not allow cycles between types. Another desirable property is that the in-method field of the node representing an instruction points back to the method containing it. We will use this second property as a running example in this section.

A.3.2 Implementation overview : subtyping, variance and phantom types

It is possible to express with Typed/Racket that a Method should contain a list of Instructions, and that Instructions should point to a MethodWe are not concerned here about the ability to create such values, which necessarily contain some form of cycle. The goal of the graph library is indeed to handle the creation and traversal of such cyclic data structures in a safe way:

«invariant-1» ::=

(struct Instruction ([opcode : Byte]
[in-method : Method]))
(struct Method ([body : (Listof Instruction)]))

This type does not, however, encode the fact that an instruction should point to the method containing it. Typed/Racket does not really have a notion of singleton types, aside from symbols and other primitive data. It also lacks a way to type "the value itself" (e.g. to describe a single-field structure pointing to itself, possibly via a Promise). This means that the property could only be expressed in a rather contrived way, if it is at all possible.

We decide to rely instead on a run-time check, i.e. a sort of contract which checks the structural invariant on the whole graph. In order to let the type-checker know whether a value was checked against that contract or not, we include within the node a phantom type which is used as a flag, indicating that the graph was checked against that contract. This phantom type in a sense refines the node type, indicating an additional property (which, in our case, is not checked at compile-time but instead enforced at run-time).

«invariant-2» ::=

(struct (Flag) Instruction ([opcode : Byte]
[in-method : (Method Flag)]))
(struct (Flag) Method ([body : (Listof (Instruction Flag))]))

We would then write a function accepting a Method for which the contract method→instruction→same-method was checked like this:

«invariant-2-use» ::=

(λ ([m : (Method 'method→instruction→same-method)])
…)

Unfortunately, this attempt fails to catch errors as one would expect, because Typed/Racket discards unused polymorphic arguments, as can be seen in the following example, which type-checks without any complaint:

«phantom-types-ignored» ::=

(struct (Phantom) S ([x : Integer]))
(define inst-sa : (S 'a) (S 1))
(ann inst-sa (S 'b))

We must therefore make a field with the Flag type actually appear within the instance:

«invariant-3» ::=

(struct (Flag) Instruction ([opcode : Byte]
                            [in-method : (Method Flag)]
                            [flag : Flag]))
(struct (Flag) Method ([body : (Listof (Instruction Flag))]
                       [flag : Flag]))

Another issue is that the flag can easily be forged. We would therefore like to wrap it in a struct type which is only accessible by the graph library:

«invariant-4» ::=

(struct (Flag) Flag-Wrapper-Struct ([flag : Flag]))
(define-type Flag-Wrapper Flag-Wrapper-Struct)
;provide only the type, not the constructor or accessor
(provide Flag-Wrapper)

We would like to be able to indicate that a graph node has validated several invariants. For that, we need a way to represent the type of a "set" of invariant witnesses. We also want some subtyping relationship between the sets: a set s₁ with more invariant witnesses should be a subtype of a subset s₂ ⊆ s₁. We can order the invariant witnesses and use Rec to build the type of a list of invariant witnesses, where some may be missing:

«invariant-set-as-List+Rec» ::=

(define-type At-Least-InvB+InvD
  (Rec R₁ (U (Pairof Any R₁)
             (Pairof 'InvB (Rec R₂ (U (Pairof Any R₂)
                                      (Pairof 'InvD (Listof Any))))))))

«invariant-set-as-List+Rec-use» ::=

(ann '(InvA InvB InvC InvD InvE) At-Least-InvB+InvD)
(ann '(InvB InvD) At-Least-InvB+InvD)
;Rejected, because it lacks 'InvD
;(ann '(InvB InvC InvE) At-Least-InvB+InvD)
;The elements must be in the right order,
;this would be rejected by the typechecker:
;(ann '(InvD InvB) At-Least-InvB+InvD)

Another solution is to group the witnesses in an untagged union with U, and place it in a contravariant position:

«invariant-set-as-contravariant-U» ::=

(define-type At-Least-InvB+InvD
(→ (U 'InvB 'InvD) Void))

In the case where no invariant is present in the untagged union, the type (U) a.k.a Nothing, the bottom type with no value, would appear. This type is somewhat pathological and allows absurd reasoning (a function accepting Nothing can never be called, which may incite the type checker to perform excessive elision). To avoid any pitfalls, we will systematically include a dummy element Or in the union, to make sure the union never becomes empty.

This solution also has the advantage that the size of the run-time witness is constant, and does not depend on the number of checked contracts (unlike the representation using a list). In practice the function should never be called. It can however simply be implemented, in a way which will match all witness types, as a function accepting anything and returning void.

In addition to testifying that a graph node was checked against multiple, separate contracts, there might be some contracts which check stronger properties than others. A way to encode this relationship in the type system is to have subtyping relationships between the contract witnesses, so that \textit{P}₁(x) ⇒ \textit{P}₂(x) ⇒ \textit{Inv}₁ <: \textit{Inv}₂:

«invariant-contract-subtyping»1 ::=

(struct InvWeak ())
(struct InvStrong InvWeak ())

If the witnesses must appear in a contravariant position (when using U to group them), the relationship must be reversed:

«invariant-contract-subtyping»2 ::=

(struct InvStrongContra ())
(struct InvWeakContra InvStrongContra ())

Alternatively, it is possible to use a second contravariant position to reverse the subtyping relationship again:

«invariant-contract-subtyping»3 ::=

(struct InvWeak ())
(struct InvStrong InvWeak ())

(define InvWeakContra (→ InvWeak Void))
(define InvStrongContra (→ InvStrong Void))

Finally, we note that the invariants should always be represented using a particular struct type, instead of using a symbol, so that name clashes are not a problem.

A.3.3 Encoding property implication as subtyping

The witness for a strong property should be a subtype of the witness for a weaker property. This allows a node with a strong property to be passed where a node with a weaker property is passed.

«structural-draft» ::=

;Draft ideas

(struct inv∈ ())
(struct inv≡ ())
(struct inv∉ ())

;(List Rel From Path1 Path2)
(List ≡ ANodeName (List f1 f2) (List))
(List ∈ ANodeName (List f1 f2) (List))
(List ∉ ANodeName (List f1 f2) (List))
(List ∉ ANodeName (List (* f1 f2 f3 f4) (* f5 f6)) (List))

;(List From Path+Rel)
(List ANodeName (List f1 f2 ≡))
(List ANodeName (List f1 f2 ∈))
(List ANodeName (List f1 f2 ∉))
(List ANodeName (List (List f1 ∉)
                      (List f2 ∉)
                      (List f3 ∉)
                      (List f4
                            (List f5 ∉)
                            (List f6 ∉))))

;; How to make it have the right kind of subtyping?

A.3.3.1 Properties applying to all reachable nodes from x

The property x ≢ x.** can be expanded to a series of properties. For example, if x has two fields a and d, the former itself having two fields b and c, and the latter having a field e, itself with a field f: «expanded-path-set» ::=

(x ≢ x.a)
(x ≢ x.a.b)
(x ≢ x.a.c)
(x ≢ x.d)
(x ≢ x.d.e)
(x ≢ x.d.e.f)

A.3.3.2 Prefix trees to the rescue

This expanded representation is however costly, and can be expressed more concisely by factoring out the prefixes.

«prefixes»1 ::=

(x ≢ (x (a (b) (c))
(d (e (f)))))

One thing which notably cannot be represented concisely in this way is x.a.** ≢ x.b.**, meaning that the subgraphs rooted at x.a and x.b are disjoint. It would be possible to have a representation combining a prefix-tree on the left, and a prefix-tree on the right, implying the cartesian product of both sets of paths. This has a negligible cost in the size of the type for the case where one of the members of the cartesian product, as we end up with the following (the left-hand-side x gains an extra pair of parentheses, because it is now an empty tree):

«prefixes»2 ::=

((x) ≢ (x (a (b) (c))
(d (e (f)))))

This does not allow concise expression of all properties, i.e. this is a form of compression, which encodes concisely likely sets of pairs of paths, but is of little help for more random properties. For example, if a random subset of the cartesian product of reachable paths is selected, there is no obvious way to encode it in a significantly more concise way than simply listing the pairs of paths one by one.

A.3.3.3 Cycles in properties

If a ** path element (i.e. a set of paths representing any path of any length) corresponds to a part of the graph which contains a cycle in the type, it is necessary to make that cycle appear in the expanded form. For that, we use Rec. Supposing that the node x has two fields, a and c, the first itself having a field b of type x. We would expand x.** to the following shape:

(Rec X (≢ (Node0 'x) (Node2 'x (Field1 'a (Field1 'b (Field1 X))) (Field1 'c))))

If one of the fields refers not to the root, but to

TODO: distinction between root nodes and fields in the path. Add an ε component at the root of each path?

A.3.3.4 Partial paths

Partial paths: if a property holds between x.a and x.b, then it is stronger than a property which holds between y.fx.a and y.fx.b (i.e. the common prefix path narrows down the set of pairs of values which are related by the property).

A possible solution idea: mask the "beginning" of the path with a ∀ or Any. Either use (Rec Ign (U (Field1 Any Ign) Actual-tail-of-type)), or reverse the “list”, so that one writes (Field1 'b (Field1 'a Any)), i.e. we have (Field1 field-name up) instead of (Field1 field-name children). The problem with the reversed version is that two child fields b and c need to refer to the same parent a, which leads to duplication or naming (in the case of naming, Typed/Racket tends to perform some inlining anyway, except if tricks are used to force the type to be recursive (in which case the subtyping / type matching is less good and fails to recognise weaker or equivalent formulations of the type)). The problem with the Rec solution for an ignored head of any length is that the number of fields is not known in advance (but hopefully our representation choices to allow weaker properties with missing fields could make this a non-problem?).

A.3.3.5 Array and list indices

When a path reaches an array, list, set or another similar collection, the special path element * can be used to indicate “any element in the array or list”. Specific indices can be indicated by an integer, or for lists with car, first, second, third and so on. The special path elements cdr and rest access the rest of the list, i.e. everything but the first element.

A.3.3.6 Other richer properties

Other richer properties can be expressed, like x.len = (length x.somelist). This property calls some racket primitives (length), and compares numeric values. However, we do not attempt to make the type checker automatically recognise weaker or equivalent properties. Instead, we simply add to the phantom type a literal description of the checked property, which will only match the same exact property.

A.3.4 Implementation

A.3.4.1 The witness value

Since all witnesses will have a type of the form (→ (U (→ invᵢ Void) …) Void), they can all be represented at run-time by a single value: a function accepting any argument and returning Void. Note that the type of the witness is normally a phantom type, and an actual value is supplied only because Typed/Racket drops phantom types before typechecking, as mentioned earlier.

«witness-value» ::=

(: witness-value (→ Any Void))
(define witness-value (λ (x) (void)))

A.3.4.2 Grouping multiple invariants

As mentioned earlier, we group invariants together using an untagged union U, which must appear in a contravariant position. We wish to express witnesses for stronger invariants as subtypes of witnesses for weaker invariants, and therefore use a second nested function type to flip again the variance direction. We always include the Or element in the union, to avoid ever having an empty union.

«Or» ::=

(struct Or ())

«grouping-invariants» ::=

(define-type-expander (Invariants stx)
  (syntax-case stx ()
    [(_ invᵢ …)
     #'(→ (U Or (→ invᵢ Void) …) Void)]))

A.3.4.3 Structural (in)equality and (non-)membership invariants

A.3.4.3.1 Invariants and their relationships

We design our typing hierarchy to allow encoding the equality, inequality, membership and non-membership between paths. A simple example would be the property :A.b.c ≡ :A.d.e, which would hold for all nodes of type A.

These paths patterns form a suffix of actual paths. Let S₁ and S₂ be two sets of pairs of suffixes. If the set of pairs of actual paths covered by S₁ is a superset the set of pairs of actual paths covered by S₂, then S₁ can be used to express a property over more pairs of actual paths, and the resulting property on the graph as a whole is therefore more precise.

Our implementation allows the concise expression of a set of paths using a template within which sections of the path may be repeated any number of times. For example, the template :A.b (.c) *.d corresponds to the set of paths containing :A.b.d, :A.b.c.d, :A.b.c.c.d and so on.

When path elements may produce a value whose type is a variant (i.e. a union of several constructors), it can be necessary to distinguish which constructor(s) the path applies to. We use a syntax inspired from that of syntax/parse for that purpose. Any point in a path can be followed by :node-name, which effectively refines the set of actual paths so that it contains only paths where the value at that point is of the given type. The syntax :A.b.c therefore indicates that the path must start on an element of type A, and follow its fields b then c. The syntax .x:T.y.z indicates paths .x.y.z, where the element accessed by .x has the type T.

The ? path element indicates that any field can be used at the given point. The syntax .x.?.y therefore indicates the paths .x.f.y, .x.g.y, .x.h.y and so on, where f, g and h are the fields of the value obtained after .x. The ? path element can be used to describe all fields, including those hidden away by row polymorphism.

It would be possible to represent sets of path concisely by reversing all these paths so that they start with their target element, and building a prefix tree. Unfortunately, Typed Racket does not currently does not automatically detect the equivalence between the types (U (Pairof A B) (Pairof A C)) and (Pairof A (U B C)). In other words, at the type level, unions do not implicitly distribute onto pairs. When a set of properties S is extended with a new property p, the resulting set of properties will be encoded as (U S p). If S is encoded as a prefix tree, p will not implicitly be merged into the prefix tree. This means that if prefix trees were to be used, extending a set of properties with a new property would give one representation, and directly encoding that set would give another representation, and the two representations would be incomparable.

We therefore represent sets of paths using a more costly representation, by making a union of all paths, without factoring out common parts.

A.3.4.4 Parsing paths

«parse»1 ::=

(begin-for-syntax
  (define (match-id rx id)
    (let ([m (regexp-match rx (identifier→string id))])
      (and m (map (λ (%) (datum->syntax id (string->symbol %) id id))
                  (cdr m)))))
  (define-syntax ~rx-id
    (pattern-expander
     (λ (stx)
       (syntax-case stx ()
         [(_ rx g …)
          #'(~and x:id
                  {~parse (g …) (match-id rx #'x)})]))))

  (define-syntax-class f+τ
    #:attributes (f τ)
    (pattern {~rx-id #px"^([^:]+):([^:]+)$" f τ})
    (pattern {~rx-id #px"^([^:]+)$" f} #:with ({~optional τ}) #'())
    (pattern {~rx-id #px"^:([^:]+)$" τ} #:with ({~optional f}) #'())
    (pattern {~rx-id #px"^:$"} #:with ({~optional (f τ)}) #'()))
  (define-syntax-class just-τ
    #:attributes (τ)
    (pattern {~rx-id #px"^:([^:]+)$" τ}))
  (define-syntax-class π-elements
    #:literals (#%dotted-id #%dot-separator)
    #:attributes ([f 1] [τ 1])
    (pattern (#%dotted-id {~seq #%dot-separator :f+τ} …)))
  (define-syntax-class extract-star
    #:literals (* #%dotted-id)
    (pattern (#%dotted-id {~and st *} . rest)
             #:with {extracted-star …} #'{st (#%dotted-id . rest)})
    (pattern other
             #:with {extracted-star …} #'{other}))
  (define-syntax-class sub-elements
    #:literals (* #%dot-separator)
    #:attributes ([f 2] [τ 2] [sub 1])
    (pattern
     (:extract-star …)
     #:with ({~either :π-elements {~seq sub:sub-elements *}} …)
            #'(extracted-star … …))))

«parse»2 ::=

(define-type-expander <~τ
  (syntax-parser
    [(_ τ) #'τ]
    [(_ f₀ . more)
     #`(f₀ (<~τ . more))]))
(begin-for-syntax
  (define-template-metafunction generate-sub-π
    (syntax-parser
      [(_ :sub-elements after)
       #:with R (gensym 'R)
       (template
        (Rec R
             (U (<~τ (?? (∀ (more) (generate-sub-π sub more))
                         (∀ (more) (List* (Pairof (?? 'f AnyField)
                                                  (?? τ AnyType))
                                          …
                                          more)))
                     …
                     R)
                after)))])))
(define-type-expander Π
  (syntax-parser
    #:literals (#%dotted-id #%dot-separator)
    [(_ {~optional (~or (#%dotted-id fst-τ:just-τ
                                     {~seq #%dot-separator fst:f+τ} …)
                        {~datum :}
                        (~and fst-τ:just-τ
                              {~parse (fst:f+τ …) #'()}))}
        . :sub-elements)
     #:with R (gensym 'R)
     (template/top-loc
      this-syntax
      (Rec R (U (Pairof Any R)
                (List* (?? (?@ (Pairof AnyField fst-τ.τ)
                               (Pairof (?? 'fst.f AnyField)
                                       (?? fst.τ AnyType))
                               …))
                       «π»))))]))

«π» ::=

(<~τ (?? (∀ (more) (generate-sub-π sub more))
         (∀ (more) (List* (Pairof (?? 'f AnyField) (?? τ AnyType))
                          …
                          more)))
     …
     Null)

«Invariant» ::=

(define-type-expander Invariant
  (syntax-parser
    #:literals (≡ ≢ ∈ ∉ ∋ ∌ = ≤ ≥ length +)
    [(_ π₁ … ≡ π₂ …) #`(U (inv≡ (Π π₁ …) (Π π₂ …))
                          (inv≡ (Π π₂ …) (Π π₁ …)))]
    [(_ π₁ … ≢ π₂ …) #`(U (inv≢ (Π π₁ …) (Π π₂ …))
                          (inv≢ (Π π₂ …) (Π π₁ …)))]
    [(_ π₁ … ∈ π₂ …) #`(inv∈ (Π π₁ …) (Π π₂ …))]
    [(_ π₁ … ∋ π₂ …) #`(inv∈ (Π π₂ …) (Π π₁ …))]
    [(_ π₁ … ∉ π₂ …)
     #`(U (inv≢ (Π π₁ …) (Π π₂ … (#%dotted-id #%dot-separator :)))
          (inv≢ (Π π₂ … (#%dotted-id #%dot-separator :)) (Π π₁ …)))]
    [(_ π₁ … ∌ π₂ …)
     #`(U (inv≢ (Π π₂ …) (Π π₁ … (#%dotted-id #%dot-separator :)))
          (inv≢ (Π π₁ … (#%dotted-id #%dot-separator :)) (Π π₂ …)))]
    ;; TODO: = should use a combination of ≤ and ≥
    [(_ π₁ …
        {~and op {~or = ≤ ≥}}
        (~or (+ (length π₂ …) n:nat)
             {~and (length π₂ …) {~parse n 0}}))
     #:with opN (syntax-case #'op (= ≤ ≥)
                  [= #'=N]
                  [≤ #'≤N]
                  [≥ #'≥N])
     #`(→ (invLength (opN n) (Π π₁ …) (Π π₂ …)) Void)]))

«=» ::=

(define-type (P A B) (Promise (Pairof A B)))
(define-type a 'a)
(define-type x 'x)
(define-type ax (U a x))
(define-type x* (Rec R (P x R)))
(define-type ax* (Rec R (P ax R)))
(define-type-expander =N
  (syntax-parser
    [(_ 0) #'x*]
    [(_ n:nat) #`(P a (=N #,(sub1 (syntax-e #'n))))]))
(define-type-expander ≥N
  (syntax-parser
    [(_ 0) #'ax*]
    [(_ n:nat) #`(P a (≥N #,(sub1 (syntax-e #'n))))]))
(define-type-expander ≤N
  (syntax-parser
    [(_ 0) #'x*]
    [(_ n:nat) #`(P ax (≤N #,(sub1 (syntax-e #'n))))]))

«Invariants» ::=

(define-type-expander Invariants
  (syntax-parser
    [(_ inv …)
     #`(→ (U Or (Invariant . inv) …) Void)]))

«Any*» ::=

(define-type AnyField Symbol);(struct AnyField () #:transparent)
(struct AnyType () #:transparent)
(define-type ε (Π))

A.3.4.4.1 Comparison operator tokens

We define some tokens which will be used to identify the operator which relates two nodes in the graph.

«comparison-operators» ::=

(struct (A B) inv≡ ([a : A] [b : B]))
(struct (A B) inv≢ ([a : A] [b : B]))
(struct (A B) inv∈ ([a : A] [b : B]))
(struct (A B C) invLength ([a : A] [b : B] [c : C]))
;(struct inv∉ ()) ;; Can be expressed in terms of ≢

(module literals typed/racket
  (define-syntax-rule (define-literals name ...)
    (begin
      (provide name ...)
      (define-syntax name
        (λ (stx)
          (raise-syntax-error 'name
                              "Can only be used in special contexts"
                              stx)))
      ...))

  (define-literals ≡ ≢ ∈ ∉ ∋ ∌ ≥ ≤))
(require 'literals)

«≡» ::=

(define-for-syntax (relation inv)
  (syntax-parser
    [(_ (pre-a … {~literal _} post-a …)
        (pre-b … {~literal _} post-b …))
     #:with (r-pre-a …) (reverse (syntax->list #'(pre-a …)))
     #:with (r-pre-b …) (reverse (syntax->list #'(pre-b …)))
     ;; Use U to make it order-independent
     #`(#,inv (U (Pairof (Cycle r-pre-a …)
                         (Cycle post-a …))
                 (Pairof (Cycle r-pre-b …)
                         (Cycle post-b …))))]))

(define-type-expander ≡x (relation #'inv≡))
(define-type-expander ≢x (relation #'inv≢))

«cycles» ::=

(struct ε () #:transparent)
(struct (T) Target ([x : T]) #:transparent)
(struct (T) NonTarget Target () #:transparent)

(define-type-expander Cycle
  (syntax-parser
    [(_ field:id … {~literal ↙} loop1:id … (target:id) loop2:id …)
     #'(→ (List* (NonTarget ε)
                 (NonTarget 'field) …
                 (Rec R (List* (NonTarget 'loop1) … ;(NonTarget 'loop1) …
                               (Target 'target) ;(NonTarget 'target)
                               (U (List* (NonTarget 'loop2) … ;(NonTarget 'loop2) …
                                         R)
                                  Null)))) Void)]
    [(_ field … target)
     #'(→ (List (NonTarget ε)
                (NonTarget 'field)
                …
                (Target 'target)) Void)]
    [(_)
     #'(→ (List (Target ε)) Void)]))

A.3.4.5 Putting it all together

«*» ::=

(require (only-in typed/dotlambda #%dotted-id #%dot-separator)
         "dot-lang.rkt"
         (for-syntax racket/base
                     racket/list
                     phc-toolkit/untyped
                     syntax/parse
                     syntax/parse/experimental/template)
         (for-meta 2 racket/base)
         (for-meta 2 phc-toolkit/untyped/aliases)
         (for-meta 3 racket/base))

(begin-for-syntax
  (define-syntax-rule #`e
    (quasisyntax/top-loc this-syntax e))
  (define-syntax-rule (template/top-loc loc e)
    (quasisyntax/top-loc loc #,(template e))))

(provide ≡ ≢ ∈ ∉ ∋ ∌ ≥ ≤)

;; For testing:
(provide Invariants
         inv≡
         inv≢
         Or
         ;Target
         ;NonTarget
         ε
         witness-value
         Π
         AnyType
         AnyField
         Invariant)

«parse»

«witness-value»
«Any*»
«comparison-operators»
«Invariant»
«Invariants»
«Or»
«=»

A.4 Compile-time graph metadata

We define here the compile-time metadata describing a graph type.

A.4.1 Graph type information

The type of a graph is actually the type of its constituent nodes. The node types may be polymorphic in the tvars type variables. The root node name and the order of the nodes are purely indicative here, as a reference to any node in the graph instance would be indistinguishable from a graph rooted in that node type.

The invariants are not enforced by the node types. Instead, the node types just include the invariant type as a witness (inside the raw field). The invariant is enforced either by construction, or with a run-time check performed during the graph creation.

«graph-info» ::=

(struct+/contract graph-info
  ([name identifier?]
   [tvars (listof identifier?)]
   [root-node identifier?]
   [node-order (listof identifier?)]
   [nodes (hash/c symbol? node-info? #:immutable #t)]
   [invariants (set/c invariant-info? #:kind 'immutable #:cmp 'equal)])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'graph-info))]
  #:property prop:custom-print-quotable 'never)

A.4.2 Graph builder information

The information about a graph type is valid regardless of how the graph instances are constructed, and is therefore rather succinct.

The graph-builder-info struct extends this with meaningful information about graph transformations. Two transformations which have the same output graph type may use different sets of mapping functions. Furthermore, the dependent-invariants are invariants relating the input and output of a graph transformation.

The multi-constructor identifier refers to a function which takes n lists of lists of mapping argument tuples, and returns n lists of lists of nodes. It is the most general function allowing the creation of instances of the graph. Wrappers which accept a single tuple of arguments and return the corresponding node can be written based on it.

«graph-builder-info» ::=

(struct+/contract graph-builder-info graph-info
  ([name identifier?]
   [tvars (listof identifier?)]
   [root-node identifier?]
   [node-order (listof identifier?)]
   [nodes (hash/c symbol? node-info? #:immutable #t)]
   [invariants (set/c invariant-info? #:kind 'immutable #:cmp 'equal)])
  ([multi-constructor identifier?]
   [root-mapping identifier?]
   [mapping-order (listof identifier?)]
   [mappings (hash/c symbol? mapping-info? #:immutable #t)]
   [dependent-invariants (set/c dependent-invariant-info?
                                #:kind 'immutable
                                #:cmp 'equal)])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'graph-builder-info))]
  #:property prop:custom-print-quotable 'never)

A.4.3 Node information

«node-info» ::=

(struct+/contract node-info
  ([predicate? identifier?]
   [field-order (listof identifier?)]
   [fields (hash/c symbol? field-info? #:immutable #t)]
   [promise-type stx-type/c]
   ;; Wrappers can mean that we have incomplete types with fewer
   ;; fields than the final node type.
   ;[make-incomplete-type identifier?]
   ;[incomplete-type identifier?])

  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'node-info))]
  #:property prop:custom-print-quotable 'never)

A.4.4 Field information

A field has a type.

«field-info» ::=

(struct+/contract field-info
  ([type stx-type/c])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'field-info))]
  #:property prop:custom-print-quotable 'never)

A.4.5 Invariant information

«invariant-info» ::=

(struct+/contract invariant-info
  ([predicate identifier?] ; (→ RootNode Boolean : +witness-type)
   [witness-type stx-type/c])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'invariant-info))]
  #:property prop:custom-print-quotable 'never
  #:methods gen:equal+hash
  «gen:equal+hash free-id-tree=?»)

Instances of invariant-info are compared pointwise with free-id-tree=?:

«gen:equal+hash free-id-tree=?» ::=

[(define equal-proc free-id-tree=?)
(define hash-proc free-id-tree-hash-code)
(define hash2-proc free-id-tree-secondary-hash-code)]

A.4.6 Dependent invariant information

The invariants described in the previous section assert properties of a graph instance in isolation. It is however desirable to also describe invariants which relate the old and the new graph in a graph transformation.

«dependent-invariant-info» ::=

(struct+/contract dependent-invariant-info
  ([checker identifier?] ; (→ RootMappingArguments… NewGraphRoot Boolean)
   [name identifier?])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'dependent-invariant-info))]
  #:property prop:custom-print-quotable 'never
  #:methods gen:equal+hash
  «gen:equal+hash free-id-tree=?»)

Instances of dependent-invariant-info are compared pointwise with free-id-tree=?, like invariant-info.

A.4.7 Mapping information

«mapping-info» ::=

(struct+/contract mapping-info
  ([mapping-function identifier?]
   [with-promises-type identifier?]
   [make-placeholder-type identifier?]
   [placeholder-type identifier?])
  #:transparent
  #:methods gen:custom-write
  [(define write-proc (struct-printer 'mapping-info))]
  #:property prop:custom-print-quotable 'never)

A.4.8 Printing

It is much easier to debug graph information if it is free from the visual clutter of printed syntax objects (which waste most of the screen real estate printing #<syntax:/path/to/file, when the interesting part is the contents of the syntax object).

We therefore pre-process the fields, transforming syntax objects into regular data.

«printer» ::=

(define (to-datum v)
  (syntax->datum (datum->syntax #f v)))

(define ((syntax-convert old-print-convert-hook)
         val basic-convert sub-convert)
  (cond
    [(set? val)
     (cons 'set (map sub-convert (set->list val)))]
    [(and (hash? val) (immutable? val))
     (cons 'hash
           (append-map (λ (p) (list (sub-convert (car p))
                                    (sub-convert (cdr p))))
                       (hash->list val)))]
    [(syntax? val)
     (list 'syntax (to-datum val))]
    [else
     (old-print-convert-hook val basic-convert sub-convert)]))

(define ((struct-printer ctor) st port mode)
  (match-define (vector name fields ...) (struct->vector st))
  (define-values (info skipped?) (struct-info st))
  (define-values (-short-name 2 3 4 5 6 7 8)
    (struct-type-info info))
  (define short-name (or ctor -short-name))
  (define (to-datum v)
    (syntax->datum (datum->syntax #f v)))
  (case mode
    [(#t)
     (display "#(" port)
     (display name port)
     (for-each (λ (f)
                 (display " " port)
                 (write (to-datum f) port))
               fields)
     (display ")" port)]
    [(#f)
     (display "#(" port)
     (display name port)
     (for-each (λ (f)
                 (display " " port)
                 (display (to-datum f) port))
               fields)
     (display ")" port)]
    [else
     (let ([old-print-convert-hook (current-print-convert-hook)])
       (parameterize ([constructor-style-printing #t]
                      [show-sharing #f]
                      [current-print-convert-hook
                       (syntax-convert old-print-convert-hook)])
         (write
          (cons short-name
                (map print-convert
                     ;; to-datum doesn't work if I map it on the fields?
                     fields))
          port)))]))

«*» ::=

(require phc-toolkit/untyped
         type-expander/expander
         racket/struct
         mzlib/pconvert
         "free-identifier-tree-equal.rkt"
         (for-syntax phc-toolkit/untyped
                     syntax/parse
                     syntax/parse/experimental/template
                     racket/syntax))

(define-syntax/parse
    (struct+/contract name {~optional parent}
      {~optional ([parent-field parent-contract] ...)}
      ([field contract] ...)
      {~optional {~and transparent #:transparent}}
      (~and {~seq methods+props ...}
            (~seq (~or {~seq #:methods _ _}
                       {~seq #:property _ _})
                  ...)))
  #:with name/c (format-id #'name "~a/c" #'name)
  (template
   (begin
     (struct name (?? parent) (field ...)
       (?? transparent)
       methods+props ...)
     (define name/c
       (struct/c name
                 (?? (?@ parent-contract ...))
                 contract ...))
     (module+ test
       (require rackunit)
       (check-pred flat-contract? name/c))
     (provide name/c
              (contract-out (struct (?? (name parent) name)
                              ((?? (?@ [parent-field parent-contract]
                                       ...))
                               [field contract]
                               ...)))))))

«printer»

«field-info»
«node-info»
«invariant-info»
«dependent-invariant-info»
«graph-info»
«mapping-info»
«graph-builder-info»

A.5 Declaring graph types

The define-graph-type form binds name to a graph-info struct. The name therefore contains metadata describing among other things the types of nodes, the invariants that instances of this graph type will satisfy.

«signature» ::=

(begin-for-syntax
  (define-syntax-class signature
    #:datum-literals (∈ ∋ ≡ ≢ ∉)
    #:literals (:)
    (pattern
     (~no-order {~once name}
                {~maybe #:∀ (tvar …)}
                {~once (~and {~seq (nodeᵢ:id [fieldᵢⱼ:id : τᵢⱼ:type]
                                             …) …}
                             {~seq [root-node . _] _ …})}
                {~seq #:invariant a {~and op {~or ∈ ∋ ≡ ≢ ∉}} b}
                {~seq #:invariant p}))))

A.5.1 Implementation

The define-graph-type macro expands to code which defines names for the node types. It then binds the given name to the graph-info instance built by build-graph-info.

«define-graph-type» ::=

(begin-for-syntax
  (define-template-metafunction (!check-remembered-node! stx)
    (syntax-case stx ()
      [(_ nodeᵢ fieldᵢⱼ …)
       (syntax-local-template-metafunction-introduce
        (check-remembered-node! #'(nodeᵢ fieldᵢⱼ …)))])))

(define-syntax/parse (define-graph-type . {~and whole :signature})
  ;; fire off the eventual delayed errors added by build-graph-info
  (lift-maybe-delayed-errors)
  #`(begin
      «declare-node-types»
      (define-syntax name
        (build-graph-info (quote-syntax whole)))))

A.5.2 Declaring the node types

«declare-node-types» ::=

(define-type nodeᵢ
  (Promise
   ((!check-remembered-node! nodeᵢ fieldᵢⱼ …) τᵢⱼ …
                                              'Database
                                              'Index)))
…

A.5.3 Creating the graph-info instance

«build-graph-info» ::=

(define-for-syntax (build-graph-info stx)
  (parameterize ([disable-remember-immediate-error #t])
    (syntax-parse stx
      [:signature
       «graph-info»])))

«graph-info» ::=

(graph-info #'name
            (syntax->list (if (attribute tvar) #'(tvar …) #'()))
            #'root-node
            (syntax->list #'(nodeᵢ …))
            (make-immutable-hash
             (map cons
                  (stx-map syntax-e #'(nodeᵢ …))
                  (stx-map (λ/syntax-case (nodeᵢ node-incompleteᵢ
                                                 [fieldᵢⱼ τᵢⱼ] …) ()
                             «node-info»)
                           #'([nodeᵢ node-incompleteᵢ
                               [fieldᵢⱼ τᵢⱼ] …] …))))
            (list->set
             (append
              (stx-map (λ/syntax-case (op a b) () «invariant-info-op»)
                       #'([op a b] …))
              (stx-map (λ/syntax-case p () «invariant-info-p»)
                       #'(p …)))))

«node-info» ::=

(node-info (meta-struct-predicate
            (check-remembered-node! #'(nodeᵢ fieldᵢⱼ …)))
           (syntax->list #'(fieldᵢⱼ …))
           (make-immutable-hash
            (map cons
                 (stx-map syntax-e #'(fieldᵢⱼ …))
                 (stx-map (λ/syntax-case (fieldᵢⱼ τᵢⱼ) ()
                            «field-info»)
                          #'([fieldᵢⱼ τᵢⱼ] …))))
           #'nodeᵢ ; promise type)

«field-info» ::=

(field-info #'τᵢⱼ)

«invariant-info-op» ::=

(invariant-info #'predicateTODO
#'witnessTODO)

«invariant-info-p» ::=

(invariant-info #'predicateTODO
#'witnessTODO)

A.5.4 Putting it all together

«*» ::=

(require racket/require
         phc-toolkit
         remember
         (lib "phc-adt/tagged-structure-low-level.hl.rkt")
         (for-syntax "graph-info.hl.rkt"
                     type-expander/expander
                     phc-toolkit/untyped
                     racket/set
                     subtemplate/override
                     extensible-parser-specifications)
         (for-meta 2 racket/base))

(provide define-graph-type)

«signature»
«build-graph-info»
«define-graph-type»

A.6 Implementation of the graph macro

«graph» ::=

(define-syntax define-graph
  (syntax-parser
    [«signature»
     «implementation»]))

«signature» ::=

(_ name
[[nodeᵢ [fieldᵢⱼ :colon τᵢⱼ] …] …]
[[(mappingₖ [argₖₗ τₖₗ] …) :colon return-typeₖ . bodyₖ] …])

«implementation» ::=

#'()

A.6.1 Overview of the implementation (draft)

«implementation-draft» ::=

«create-Qₖ»
«re-bind-mappings»
«define-indices»
«process-queues»

«define-indices» ::=

(define/with-syntax (indexₖ …) (stx-map gensym #'(idxₖ …)))
#'(begin
(define-type indexₖ (graph-index 'indexₖ))
…)

«define-index» ::=

(struct (K) graph-index ([key : K] [index : Index]))

Create one queue Qₖ for each mapping:

«create-Qₖ» ::=

#'(begin
    (define Qₖ <create-queue>)
    (define Qₖ-enqueue <TODO>)
    (define Qₖ-pop <TODO>)
    …)

Re-bind mappings to catch outbound calls:

«re-bind-mappings» ::=

#'(let ([mappingₖ make-placeholderₖ] …)
. bodyₖ)

Define functions which enqueue into a given Qₖ and start processing. The final name macro dispatches to these functions.

«entry-pointₖ» ::=

#'(begin
    (define (entry-pointₖ argₖₗ …)
      (entry-point #:mappingₖ (list (list argₖₗ …))))
    …)

These are based upon the main entry-point, which takes any number of initial elements to enqueue, and processes the queues till they are all empty.

«entry-point» ::=

#'(define (entry-point #:mappingₖ [argsₖ* : (Listof (List τₖₗ …)) '()])
    (for ([argsₖ (in-list argsₖ*)])
      (let-values ([(argₖₗ …) argsₖ])
        (Qₖ-enqueue argₖₗ …))))

«process-queues» ::=

(until queues are all empty
process item,see below)

Find and replace references to old nodes and new incomplete nodes and new placeholder nodes, instead insert indices.
Problem: we need to actually insert indices for references to nodes, not for references to mappings (those have to be inlined).

«*» ::=

(require racket/require
         (for-syntax (subtract-in racket/base
                                  subtemplate/override)
                     phc-toolkit/untyped
                     type-expander/expander
                     subtemplate/override)
         "traversal.hl.rkt"
         phc-toolkit)
«define-index»
«graph»

A.7 Draft of the implementation of the graph macro

«overview»1 ::=

(define low-graph-impl
  (syntax-parser
    [«signature+metadata»
     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
     «phase 1: call mappings and extract placeholders»
     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
     «phase 2: inline placeholders within node boundaries»
     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
     «phase 3: replace indices with promises»
     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
     «equality-coalescing»
     «invariants+auto-fill»
     «inflexible-row-polymorphism»
     «flexible-row-polymorphism»
     «polymorphic-node-types-and-mappings»
     ;<general-purpose-graph-algorithms>
     ;<garbage-collection>

     «phase~1: call mappings and extract placeholders»]))

«signature+metadata» ::=

«signature»
«metadata»

«signature» ::=

(_ graph-name
   #:∀ (pvarₕ …)
   ({~lit node} nodeᵢ [fieldᵢⱼ cᵢⱼ:colon field-τᵢⱼ] …)
   …
   ({~lit mapping} (mappingₖ [argₖₗ :colon arg-τₖₗ] …)
                   :colon result-τₖ
                   . bodyₖ)
   …)

«metadata» ::=

(void)

«phase 1: call mappings and extract placeholders»1 ::=

'<worklist>
'<call-mapping-functions+placeholders>
'<extract-placeholders> ;; and put them into the worklist

«phase~1: call mappings and extract placeholders» ::=

#'(begin
    (define
      #:∀ (pvarₕ …)
      (graph-name [rootₖ : (Listof (List arg-τₖₗ …))] …)

      ;; TODO: move these to a separate literate programming chunk
      (define-type nodeᵢ (tagged nodeᵢ [fieldᵢⱼ cᵢⱼ field-τᵢⱼ] …))
      …

      (define (make-placeholderₖ argₖₗ …)
        (list 'placeholderₖ argₖₗ …))
      …

      (worklist
       (list rootₖ …)
       ((λ ([args : (List arg-τₖₗ …)])
          (define-values (argₖₗ …) (apply values args))
          (define result
            (let* ([mappingₖ make-placeholderₖ]
                   …
                   [argₖₗ 'convert-inflexible-to-flexible?]
                   …
                   [argₖₗ 'invariant-well-scopedness?]
                   …)
              (error "NOT IMPL YET.787543")
              ;. bodyₖ
              '(bodyₖ)))
          ;; returns placeholders + the result:
          '(extract-placeholders result)
          (error "NOT IMPL YET.8946513648"))
        …)
       ((List arg-τₖₗ …) result-τₖ) …)))

«phase 1: call mappings and extract placeholders»2 ::=

;; Phase 1: call the mapping functions on the input data
#'(: phase-1 (∀ (pvarₕ …) ;; or use this? (nodes-pvar … mapping-pvar … …)
                (→ (List (Listof mapping-arg-type) ddd)
                   (List (Listof mapping-result-type) ddd))))
#'(begin
    ;; Maybe this should be done last, when all phases are available?
    (define (phase1-many-roots (argₖₗ …) …) 'TODO)
    (define (phase1-single-root-for-mapping (argₖₗ …)) 'TODO)
    …)

«phase 2: inline placeholders within node boundaries» ::=

;; Phase 2: inline placeholders within node boundaries
'(generate-worklist
  nodes
  #'(…?))
'{(funcion which for a mapping-result → inserts nodes into worklist) …}
'(for the root mapping results
   call the function to insert nodes and keep the surrounding part)
'(for each mapping result
   call the function to insert nodes)

«phase 3: replace indices with promises» ::=

;; Phase 3: Replace indices with promises
;; Phase 3a: have an empty set of invariant witnesses, and call the
;; invariants for checking
;; Phase 3b: have the full set of invariant witnesses.
;; TODO phase 3: auto-fill.
(void)

«equality-coalescing» ::=

;; implement as always-#f-unless-eq? for now
(void)

«invariants+auto-fill» ::=

(void)

«inflexible-row-polymorphism» ::=

(void)

«flexible-row-polymorphism» ::=

(void)

«polymorphic-node-types-and-mappings» ::=

(void)

«overview»2 ::=

; high-level graph API:

Row polymorphism: make a generic struct->vector and vector->struct?

«*» ::=

(provide low-graph-impl
         (for-template (all-from-out "literals.rkt")))

(require (for-template (only-meta-in 0 type-expander/lang)
                       typed-worklist
                       phc-adt)
         type-expander/expander
         phc-toolkit/untyped/aliases
         phc-toolkit/untyped/syntax-parse
         subtemplate/override)

(require (for-template "literals.rkt"))
«overview»

A.8 Generalised constructor functions for flexible structures

«*» ::=

(provide builder-τ
         propagate-τ
         oracle
         builder-f)

(require racket/require
         (for-syntax (subtract-in racket/base subtemplate/override)
                     syntax/stx
                     racket/list
                     racket/function
                     subtemplate/override)
         (for-meta 2 racket/base)
         "binarytree.hl.rkt")

«propagate-τ»
«oracle-τ»
«oracle»
«builder-τ»
«builder-f»

We first define the builder function’s type. Since this type is rather complex, we define it using a macro. The type expander takes two arguments. The first argument n indicates the total number of fields which appear in the program (i.e. on the number of leaves of the generated tree type), and the second argument m indicates how many key/value pairs the function accepts.

«builder-τ» ::=

(define-type-expander builder-τ
  (syntax-parser
    [(_ n m)
     «builder-τ-with-1»
     «builder-τ-with-2»
     «builder-τ-with-3»
     #'«builder-function-type″»]))

We start by defining a few syntax pattern variables which will be used in the later definitions. The lists Nᵢ and Mⱼ range over the field and argument indices, respectively:

«builder-τ-with-1» ::=

#:with (Nᵢ …) (range n)
#:with (Mⱼ …) (range m)

The builder function takes a number of keys and values, and builds a (promise for) a binary tree where the leaves corresponding to those keys contain given value, and other leaves contain None. We could write (a simplified form of) the builder function type as follows:

«builder-function-type» ::=

(∀ ({?@ Kⱼ Xⱼ} …)
   (→ ;; Keys and values:
      {?@ (∩ Kⱼ (U 'NSymⱼᵢ …)) Xⱼ} …
      ;; Result type:
      (BinaryTree (Promise «Some or None») …)))

We expect each key Kⱼ to be a symbol of the shape |0|, |1|, |2| and so on:

«builder-τ-with-2» ::=

#:with (NSymᵢ …) ((string->symbol (format "~a" Nᵢ)) …)
#:with ((NSymⱼᵢ …) …) (map (const (NSymᵢ …)) (Mⱼ …))

The type of each leaf of the binary tree should be (Some Xⱼ) if a corresponding Kⱼ matches the leaf name, and None otherwise.

«Some or None» ::=

(U «(Some Xⱼ) if Kⱼ = NSymᵢ»
«None if ∀ k ∈ Kⱼ , k ≠ NSymᵢ»)

This type-level conditional is achieved via a trick involving intersection types. The Kⱼ type should be a singleton type containing exactly one of the 'NSymᵢ … symbols. For a given leaf with index i, if the Kⱼ key is the type 'NSymᵢ, then the intersection type (∩ Kⱼ 'NSymᵢ) is 'NSymᵢ. Conversely, if the Kⱼ key is not 'NSymᵢ, the intersection will be the bottom type Nothing. No values inhabit the bottom type, and Typed Racket can determine that there is no pair whose first (or second) element has the type Nothing, since no concrete value could be used to construct such a pair.

«(Some Xⱼ) if Kⱼ = NSymᵢ» ::=

(Pairof (∩ Kᵢⱼ 'NSymᵢⱼ)
Xᵢⱼ)
…

where Kᵢⱼ, Xᵢⱼ and NSymᵢⱼ are defined as follows:

«builder-τ-with-3»1 ::=

#:with ((Kᵢⱼ …) …) (map (const #'(Kⱼ …)) (Nᵢ …))
#:with ((Xᵢⱼ …) …) (map (const #'(Xⱼ …)) (Nᵢ …))
#:with ((NSymᵢⱼ …) …) (map λni.(map (const ni) (Xⱼ …)) (NSymᵢ …))

We use this fact to construct a pair above. Its first element is either 'NSymᵢ when Kⱼ is 'NSymᵢ, and Nothing otherwise. The second element of the pair contains our expected (Some Xⱼ) type, but the whole pair is collapsed to Nothing when Kⱼ is not 'NSymᵢ.

We use a similar approach to conditionally produce the None element (which we represent as #f), but instead of intersecting Kⱼ with 'NSymᵢ, we intersect it with the complement of 'NSymᵢ. Typed Racket lacks the possibility to negate a type, so we manually compute the complement of 'NSymᵢ in the set of possible keys (that is, 'NSymᵢ …).

«builder-τ-with-3»2 ::=

#:with NSyms (NSymᵢ …)
#:with Ms (Mⱼ …)
#:with (exceptᵢ …) ((remove NSymᵢ NSyms) …)
#:with (((exceptᵢⱼ …) …) …) ((map (const exceptᵢ) Ms) …)

If Kⱼ is Nᵢ, then {∩ Kⱼ {U . exceptᵢ}} will be Nothing. We take the Cartesian product of the intersections by building a List out of them. A single occurrence of Nothing will collapse the whole list to Nothing, because the Cartesian product of the empty set and any other set will produce the empty set.

The resulting type should therefore be Nothing only if there is no Kⱼ equal to Nᵢ, and be the list of symbols (List . exceptᵢ) otherwise.

«None if ∀ k ∈ Kⱼ , k ≠ NSymᵢ» ::=

(Pairof #f (List {∩ Kᵢⱼ {U 'exceptᵢⱼ …}} …))

This approach relies on the fact that occurrences of Nothing within structs and pairs containing collapse the entire struct or pair type to Nothing. Unfortunately, current versions of Typed Racket perform this simplification step in some situations but not others:

It simplifies polymorphic types when they are defined;
When a polymorphic type is instantiated, the parts which are directly affected by the intersection with a polymorphic type variable are subject to this simplification;
However, occurrences of Nothing which occur as a result of instantiating the type variable do not propagate outside of the intersection itself. This means that given the following type:
(define-type (Foo A) (U (Pairof (∩ Integer A) String) Boolean))
its instantiation (Foo Symbol) will produce the type (U (Pairof Nothing String) Boolean), but this type will not be simplified to (U Nothing Boolean) or equivalently to Boolean.

To force Typed Racket to propagate Nothing outwards as much as we need, we intersect the whole form with a polymorphic type A:

«builder-function-type′»1 ::=

(∀ (A {?@ Kⱼ Xⱼ} …)
   (→ ;; Keys and values:
      {?@ (∩ Kⱼ (U 'NSymⱼᵢ …)) Xⱼ} …
      ;; Result type:
      (BinaryTree (Promise (∩ «Some or None» A)) …)))

The type propagate-τ defined below is used to instantiate A, and is carefully picked so that its intersection will in no way change the result type (i.e. the intersection with A will be an identity operation where it is used). In other words, propagate-τ has the same shape as the leaves of the binary tree. This intersection however forces the simplification step to be performed on the affected parts once the type is instantiated.

«propagate-τ» ::=

(define-type propagate-τ
(U (Pairof Symbol Any)
(Pairof #f (Listof Symbol))))

The implementation of the builder function will need to convert values with the «Some or None» type to values of type (∩ «Some or None» A). Since the intersection could, in principle, be any subtype of «Some or None», we request that the caller supplies a proof that the conversion is possible. This proof takes the form of an oracle function, which transforms an element with the type propagate-τ (which is a supertype of every possible «Some or None» type) into an element with the type (∩ A B), where B is the original type of the value to upgrade.

«oracle-τ» ::=

(define-type (oracle-τ A)
  (∀ (B) (→ (∩ B
               (U (Pairof Symbol Any)
                  (Pairof #f (Listof Symbol))))
            (∩ A B))))

The oracle does nothing more than return its argument unchanged:

«oracle» ::=

(: oracle (oracle-τ propagate-τ))
(define (oracle v) v)

We update the builder function type to accept an extra argument for the oracle:

«builder-function-type″»1 ::=

(∀ (A {?@ Kⱼ Xⱼ} …)
   (→ ;; Oracle:
      (oracle-τ A)
      ;; Keys and values:
      {?@ (∩ Kⱼ (U 'NSymⱼᵢ …)) Xⱼ} …
      ;; Result type:
      (BinaryTree (Promise (∩ «Some or None» A)) …)))

«builder-f» ::=

(define-syntax builder-f
  (syntax-parser
    [(_ name n m)
     «builder-τ-with-1»
     «builder-τ-with-2»
     «builder-τ-with-3»
     «builder-τ-with-4»
     #'(begin «builder-function-implementation»)]))

«builder-τ-with-4» ::=

#:with ((kᵢⱼ …) …) (map (const #'(kⱼ …)) (Nᵢ …))
#:with ((xᵢⱼ …) …) (map (const #'(xⱼ …)) (Nᵢ …))

«builder-function-implementation» ::=

(: name «builder-function-type″»)
(define (name oracle {?@ kⱼ xⱼ} …)
  (list (delay
          (cond
            [((make-predicate 'NSymᵢⱼ) kᵢⱼ)
             ((inst oracle (Pairof (∩ Kᵢⱼ 'NSymᵢⱼ) Xᵢⱼ)) (cons kᵢⱼ xᵢⱼ))]
            …
            [else
             ((inst oracle (Pairof #f (List (∩ Kᵢⱼ (U 'exceptᵢⱼ …)) …)))
              (cons #f (list kᵢⱼ …)))]))
        …))

B Algebraic Data Types for compilers: Implementation

Suzanne Soy <racket@suzanne.soy>

This library is implemented using literate programming. The implementation details are presented in the following sections. The user documentation is in the Algebraic Data Types for compilers document.

B.1 Algebraic Data Types

B.1.1 A note on polysemy

B.1.2 Introduction

B.1.3 Remembered data types and pre-declarations

B.1.4 The initialisation process

B.1.5 Tagged structures, untagged structures, constructors, and variants

B.2 Low-level implementation of tagged structures

B.2.1 Overview

B.2.2 Implementation using Racket structs

B.2.2.1 Nodes as subtypes of their corresponding tagged struct type

B.2.3 Common ancestor to all tagged structures: TaggedTop-struct

B.2.4 Printing and comparing structures and nodes

B.2.4.1 Printing tagged structures

B.2.5 Comparing tagged structures

B.2.6 Pre-declaring structs

B.2.6.1 Why pre-declare the structs?

B.2.6.2 Remembering tagged structures across compilations

B.2.6.3 Sorting the set of fields

B.2.6.4 Not-yet-remembered structs should cause an error

B.2.7 Creating instances of a tagged structure

B.2.8 Predicate for a tagged structure

B.2.8.1 A predicate over the contents of the fields

B.2.9 Matching against tagged structures

B.2.10 Type of a tagged structure

B.2.11 Accessing fields of tagged structures

B.2.12 Row polymorphism

B.2.12.1 Type for any tagged structure containing a given set of fields

B.2.12.2 Changing the tag of a tagged structure

B.2.12.3 Splitting a tagged structure

B.2.12.4 Merging two tagged structures

B.2.12.5 Updating a tagged structure

B.2.13 Putting it all together

B.3 Implementation of nodes: printing and equality

B.3.1 Printing nodes

B.3.2 Comparing and hashing nodes

B.3.2.1 Hashing nodes

B.3.2.2 Caching node equality

B.3.2.3 Comparing nodes for equality

Bibliography

B.4 Implementation of ADTs: syntax scopes

B.4.1 Putting it all together

B.5 User API for tagged structures

B.5.1 Overview of the implementation of structures

B.5.2 A polyvalent identifier: type, match, constructor and instance

B.5.3 The tagged call expander (builder and instance)

B.5.3.1 Call to tagged with no fields: instance or constructor?

B.5.3.2 Signature for the tagged call expander

B.5.3.3 Implementation

B.5.4 Type expander

B.5.4.1 The TaggedTop type

B.5.5 Match expander

B.5.6 Predicates for tagged structures

B.5.6.1 The TaggedTop? predicate

B.5.7 Defining shorthands with define-tagged

B.5.8 Implementation of uniform-get

B.5.9 Putting it all together

B.6 Supertypes of tagged structures

B.6.1 type-expander

B.6.2 Match

B.6.3 Nested supertype

B.6.4 Conclusion

B.7 User API for untagged structures

B.7.1 Introduction

B.7.2 Defining untagged structures with define-structure

B.7.3 Implementation of StructureTop and StructureTop?

B.7.4 Supertypes for structures

B.7.5 Putting it all together

B.8 User API for constructors

B.8.1 Introduction

B.8.2 The polyvalent identifier constructor: type, match, builder and instance

B.8.3 Type-expander

B.8.4 Match-expander

B.8.5 Predicate

B.8.6 Instance creation

B.8.7 Defining shorthands for constructors with define-constructor

B.8.8 Miscellanea

B.8.9 Putting it all together

B.9 User API for variants

B.9.1 Introduction

B.9.2 Implementation of variant

B.9.3 Predicate

B.9.4 define-variant

B.9.5 Conclusion

B.10 Somewhat outdated overview of the implementation choices for structures, graphs and passes

B.10.1 Structures

B.10.2 Passes, subtyping and tests

B.10.3 Graphs

B.10.4 Conclusion

B.1 Algebraic Data Types

B.1.1 A note on polysemy

B.1.2 Introduction

B.1.3 Remembered data types and pre-declarations

B.1.4 The initialisation process

B.1.5 Tagged structures, untagged structures, constructors, and variants

B.1.1 A note on polysemy

The name “constructor” usually designates two things:

A tagged value, like the ones created or accessed using the constructor macro defined in User API for constructors
A constructor function or macro for some kind of data structure, which is the function or macro used to create instances of that data structure.

Since this could lead to ambiguities, we clarify by saying “constructor” in the former case, and “builder” or “builder function” in the latter case.

B.1.2 Introduction

We define variants (tagged unions), with the following constraints:

A constructor is described by a tag name, followed by zero or more values. Likewise, a tagged structure is described by a tag name, followed by zero or more field names, each field name being mapped to a value.
Two different variants can contain the same constructor or tagged structure, and it is not possible to create an instance of that constructor or tagged structure that would belong to one variant but not the other.
Constructors and tagged structures are "anonymous": it is not necessary to declare a constructor or tagged structure before creating instances of it, expressing its type, or using it as a match pattern.
Constructors types and tagged structures types are "interned": two constructors with the same tag name have the same type, even if they are used in different files. The same applies to two tagged structures with the same tag name and field names: even if they are used in different files, they have the same type.

The datatype package by Andrew Kent also implements Algebraic Data Types. The main differences are that unlike our library, data structures have to be declared before they are used (they are not "anonymous"), and a given constructor name cannot be shared by multiple unions, as can be seen in the example below where the second define-datatype throws an error:

Examples:

> (require datatype)
> (define-datatype Expr
    [Var (Symbol)]
    [Lambda (Symbol Expr)]
    [App (Expr Expr)])
> (define-datatype Simple-Expr
    [Var (Symbol)]
    [Lambda (Symbol Expr)])
eval:3:0: define-datatype: variant type #<syntax:eval:3:0
Var> already bound
  in: Simple-Expr

B.1.3 Remembered data types and pre-declarations

This library works by remembering all the constructors and all the tagged structures across compilations. More precisely, each constructor’s tag name is written to a file named "adt-pre-declarations.rkt" in the same directory as the user code. The tag name and list of fields of each tagged structure is also written in the same file.

The generated "adt-pre-declarations.rkt" file declares a struct for each tagged structure and constructor, so that all user files which require the same "adt-pre-declarations.rkt" will share the same struct definitions.

User files which make use of the phc-adt should include a call to adt-init before using anything else. The adt-init macro requires the "adt-pre-declarations.rkt" file, and records the lexical context of that require, so that the other macros implemented by this library can fetch the pre-declared struct types from the correct lexical scope. The "ctx.hl.rkt" file takes care of recording that lexical scope, while "adt-init.rkt" performs the initialisation sequence (creating the "adt-pre-declarations.rkt" file if it does not exist, loading the pre-declared struct types from "adt-pre-declarations.rkt", and using a utility from "ctx.hl.rkt" to record the lexical context).

«require-modules»1 ::=

(require "ctx.hl.rkt")

B.1.4 The initialisation process

The initialisation process can be somewhat complex: the directives (remember-output-file "adt-pre-declarations.rkt"), (set-adt-context) and (require "adt-pre-declarations.rkt") have to be inserted in the right order, and the file "adt-pre-declarations.rkt" has to be initialised with the appropriate contents when it does not exist. The adt-init macro defined in ""adt-init.rkt"" takes care of these steps.

«require-modules»2 ::=

(require "adt-init.rkt")

The generated "adt-pre-declarations.rkt" file will call the pre-declare-all-tagged-structure-structs macro defined in "tagged-structure-low-level.hl.rkt".

B.1.5 Tagged structures, untagged structures, constructors, and variants

We first define a low-level interface for tagged structures in the "tagged-structure-low-level.hl.rkt" file. This low-level interface includes for-syntax functions for expressing the type of tagged structures, creating builder functions for them, as well as match patterns. It also includes means to access the value of a given field on any tagged structure which contains that field. The "tagged.hl.rkt" file provides syntactic sugar for this low-level interface, and defines the tagged identifier, which acts as a type expander, match expander and macro. The macro can be used to create builder functions which return instances of tagged structures, or to directly create such instances.

«require-modules»3 ::=

(require "tagged.hl.rkt")

The ""tagged-supertype.hl.rkt"" file defines a few operations implementing some form of "static duck typing": As a type expander, (tagged-supertype fieldᵢ …) expands to the union type of all tagged structures containing a superset of the given set of fields. As a match expander, (tagged-supertype [fieldᵢ patᵢⱼ …] …) expands to a match pattern which accepts any tagged structure with a superset of the given set of fields, as long as the value of each fieldᵢ matches against all of the corresponding patᵢⱼ ….

«require-modules»4 ::=

(require "tagged-supertype.hl.rkt")

We then define untagged structures, which are tagged structures with the untagged tag name. Untagged structures can be used conveniently when the tag name is not important and the goal is simply to map a set of field names to values. The "structure.hl.rkt" file defines the structure type expander, match expander and macro. The structure identifier acts as a simple wrapper around tagged which supplies untagged as the tag name.

«require-modules»5 ::=

(require "structure.hl.rkt")

Constructors are defined as tagged structures containing a single field, called values. The constructor macro, defined in ""constructor.hl.rkt"" accepts a rich syntax for creating constructor instances containing multiple values, associated with the tag name. The values are aggregated in a list, which is stored within the values field of the tagged structure used to implement the constructor. The constructor identifier is therefore nothing more than syntactic sugar for tagged. It relies on the xlist library, which provides a rich syntax for expressing the complex list types, as well as the corresponding match pattern.

«require-modules»6 ::=

(require "constructor.hl.rkt")

For convenience, we write a variant form, which is a thin wrapper against the union type of several constructors and tagged structures, (U constructor-or-tagged …).

«require-modules»7 ::=

(require "variant.hl.rkt")

Finally, we directly include the row polymorphism features from "tagged-structure-low-level.hl.rkt":

«require-modules»8 ::=

(require "tagged-structure-low-level.hl.rkt")

«*» ::=

(begin «require-modules»)
(provide adt-init
         tagged
         tagged?
         define-tagged
         TaggedTop
         TaggedTop?
         tagged-supertype
         tagged-supertype*

         structure
         structure?
         define-structure
         StructureTop
         StructureTop?
         structure-supertype

         constructor
         constructor?
         define-constructor
         ConstructorTop
         ConstructorTop?

         variant
         define-variant

         constructor-values
         uniform-get

         split

         merge

         with+
         with!
         with!!)

B.2 Low-level implementation of tagged structures

B.2.1 Overview

B.2.2 Implementation using Racket structs

B.2.2.1 Nodes as subtypes of their corresponding tagged struct type

B.2.3 Common ancestor to all tagged structures: TaggedTop-struct

B.2.4 Printing and comparing structures and nodes

B.2.4.1 Printing tagged structures

B.2.5 Comparing tagged structures

B.2.6 Pre-declaring structs

B.2.6.1 Why pre-declare the structs?

B.2.6.2 Remembering tagged structures across compilations

B.2.6.3 Sorting the set of fields

B.2.6.4 Not-yet-remembered structs should cause an error

B.2.7 Creating instances of a tagged structure

B.2.8 Predicate for a tagged structure

B.2.8.1 A predicate over the contents of the fields

B.2.9 Matching against tagged structures

B.2.10 Type of a tagged structure

B.2.11 Accessing fields of tagged structures

B.2.12 Row polymorphism

B.2.12.1 Type for any tagged structure containing a given set of fields

B.2.12.2 Changing the tag of a tagged structure

B.2.12.3 Splitting a tagged structure

B.2.12.4 Merging two tagged structures

B.2.12.5 Updating a tagged structure

B.2.13 Putting it all together

B.2.1 Overview

A tagged structure is a data structure associating fields with their value. Two tagged structure types with the same set of fields can be distinguished by their tag. Compared to the traditional algebraic data types, a tagged structure acts like (traditional) structure wrapped in a (traditional) constructor.

Tagged structures are the central data type of this library.

Tagged structures can be used as-is.
Constructors which tag multiple values can be created by aggregating those values, and storing them within a tagged structure containing a single field named “values”.
Untagged structures can be created by implicitly supplying a default tag, which is the same for all untagged structures. In our case, the default tag is named untagged.
Nodes are implemented exactly like tagged structures, except that the contents of their fields are wrapped in promises. The promises allow creating data structures that contain cycles in appearance, despite being built exclusively using purely immutable primitives.

In order to implement field access in a way that works for tagged structures and nodes alike, it is desirable that their implementation has the same shape. We therefore also wrap the contents of tagged structure fields with promises. While the promises present within nodes do perform some kind of computation each time they are forced, the promises present within tagged structures simply return an already-known value.

B.2.2 Implementation using Racket structs

A tagged structure is implemented as a Racket struct, in which every field has a distinct polymorphic type.

«define-tagged» ::=

(struct/props (fieldᵢ/τ …) tagged-struct common-struct ()
              #:property prop:custom-write
              (make-writer common-struct name fieldᵢ …)

              #:property prop:equal+hash
              (make-comparer common-struct tagged-struct name
                             fieldᵢ …))

Tagged structures with different tag names but the same set of fields are implemented as descendant structs of a common one. The common struct contains all the fields, and the descendants only serve to distinguish between the different tag names.

«define-common» ::=

(struct/props (fieldᵢ/τ …) common-struct TaggedTop-struct
([fieldᵢ : (Promise fieldᵢ/τ)] …))

It is desirable that all data structures (tagged structures and nodes) have the same shape. This makes it easier to access the value of a given field, without having two different field access operators (one for tagged structure and one for nodes). Since nodes need to have the contents of each field wrapped within a Promise, we will also impose this on tagged structures and their derivatives (untagged structures and constructors). Although the promises used in nodes will actually perform some work, the promises in other data structures will simply wrap an already-computed value. The operator accessing a field’s contents will therefore access the desired field, and force the promise contained within, in order to obtain the real value.

B.2.2.1 Nodes as subtypes of their corresponding tagged struct type

Nodes are implemented as subtypes of their corresponding tagged struct type.

«define-node» ::=

(struct/props (fieldᵢ/τ … raw-D/τ raw-I/τ)
              node-struct
              tagged-struct
              ([raw : (raw-node raw-D/τ raw-I/τ)])
              #:property prop:custom-write
              (make-node-writer common-struct
                                name
                                fieldᵢ …)
              #:property prop:equal+hash
              (make-node-comparer common-struct
                                  node-struct
                                  name
                                  fieldᵢ …))

They contain an extra raw field, which contains a raw representation of the node consisting of a tuple of two elements: the graph’s database of nodes, and an index into that database).

(struct (Database) raw-node ([database : Database] [index : Index]))

B.2.3 Common ancestor to all tagged structures: TaggedTop-struct

struct
(struct TaggedTop-struct ()
#:extra-constructor-name make-TaggedTop-struct)

We define the TaggedTop-struct struct as the parent of every “common” struct.

«TaggedTop» ::=

(struct TaggedTop-struct () #:transparent)

The hierarchy is therefore as follows:

The struct for a node is a subtype of the struct for the tagged structure with the same name and fields.
The struct for a tagged structure is a subtype of the “common” struct which has the same set of fields. All tagged structures with the same fields but distinct tag names are implemented as subtypes of their “common” struct.
TaggedTop-struct is the direct supertype of all “common” struct. Transitively, TaggedTop-struct is therefore also a supertype of the structs corresponding to every tagged structure and node.

B.2.4 Printing and comparing structures and nodes

The data types defined in this library have a custom printed representation, and have a custom implementation of equality.

The following sections present how tagged structures are printed and compared. Nodes are described in a separate section, Implementation of nodes: printing and equality. Their behaviour differs slightly from how tagged structures are printed and compared, as they need to take into account the presence of logical cycles in the data structure. Node printing is explained in the section Printing nodes, and node equality is explained in the section Comparing and hashing nodes.

B.2.4.1 Printing tagged structures

Tagged structures are printed in different ways depending on their fields:

If the tagged structure only contains a single field whose name is “values”, then it is printed as (constructor name value …).
Otherwise, if the tagged structure’s tag name is untagged, it is printed as (structure name [field value] …).
Finally, it the tagged structure does not fall in the above two cases, it is printed as (tagged name [field value] …).

«custom-write» ::=

(define-syntax/parse (make-writer pid name fieldᵢ …)
  (define fields (map syntax-e (syntax->list #'(fieldᵢ …))))
  (define has-values-field? (member 'values fields))
  (define has-other-fields? (not (null? (remove 'values fields))))
  (define untagged? (eq? (syntax-e #'name) 'untagged))

  (define/with-syntax e
    (cond
      [untagged?
       #'(format "(structure ~a)"
                 (string-join (list «format-field» …) " "))]
      [(and has-values-field? (not has-other-fields?))
       #'`(constructor name
                       . ,(force ((struct-accessor pid values) self)))]
      [else
       #'(format "(tagged ~a ~a)"
                 'name
                 (string-join (list «format-field» …) " "))]))

  #'(λ (self out mode)
      (display e out)))

Each field is formatted as [fieldᵢ valueᵢ]. The whole printed form is built so that copy-pasting it yields a value which is equal? to the original.

«format-field» ::=

(format "[~a ~a]" 'fieldᵢ (force ((struct-accessor pid fieldᵢ) self)))

B.2.5 Comparing tagged structures

Tagged structures are compared by recursively applying equal? to their fields, after forcing the promise wrapping each field. Forcing these promises is safe, as the result of these promises is already known when creating the tagged structure. The promises are present only to ensure that tagged structures and nodes have the same shape, but cannot by themselves create logical cycles.

«equal+hash» ::=

(define-syntax/parse (make-comparer pid id name fieldᵢ …)
  #'(list (λ (a b rec-equal?)
            (and ((struct-predicate id) a)
                 ((struct-predicate id) b)
                 (rec-equal? (force ((struct-accessor pid fieldᵢ) a))
                             (force ((struct-accessor pid fieldᵢ) b)))
                 …
                 #t))
          (λ (a rec-hash)
            (bitwise-xor (rec-hash 'id)
                         (rec-hash (force ((struct-accessor pid fieldᵢ) a)))
                         …))
          (λ (a rec-hash)
            (bitwise-xor (rec-hash 'id)
                         (rec-hash (force ((struct-accessor pid fieldᵢ) a)))
                         …))))

B.2.6 Pre-declaring structs

B.2.6.1 Why pre-declare the structs?

We wish to pre-declare a Racket struct type for all tagged structures used in the program. This requirement is needed to achieve several goals:

To allow on-the-fly declaration. Otherwise, it would be necessary to be in a module-begin context to be able to declare a struct.It is possible in untyped Racket to declare a struct within an internal-definition context, however it is not possible in Typed Racket due to bug #192. Furthermore, the declaration would not be visible outside the let. This means that, within an expression, it would be impossible to create an instance of a structure which was not previously declared.
To enable "interned" tagged structures, i.e. two tagged structures with the same name and fields used in two different files are compatible, just as prefab structs.
If we use (get-field s b) in module A, and define a struct type with a field b in module B, then the module A would have to require B, in order to have access to the struct metadata, and this could easily create cyclic dependencies.
Moving the struct definition to a third file solves that problem.

We do not however wish to remember the type of each field. Indeed, the type may contain type identifiers which are not exported by the module using the tagged structure. Instead, we declare parametric structs, using a distinct type argument for each field. The struct can then be instantiated with the correct types where needed.

«pre-declare-all-tagged-structure-structs»1 ::=

(define-syntax (pre-declare-all-tagged-structure-structs stx)
  (define/with-parse (([name₁:id fieldᵢ:id …] [nameⱼ:id . _] …) …)
    (group-by (∘ list->set cdr)
              «all-remembered-tagged-structures»
              set=?))
  #`(begin
      (require (submod (lib "phc-adt/tagged-structure-low-level.hl.rkt")
                       pre-declare)
               phc-toolkit)
      (pre-declare-group [name₁ nameⱼ …] [fieldᵢ …])
      …))

«pre-declare-all-tagged-structure-structs»2 ::=

(define-syntax/parse (pre-declare-group [name:id …] [fieldᵢ:id …])

  (define/with-syntax common-struct
    (make-struct-identifier-common #f #'(fieldᵢ …)))

  (define-temp-ids "~a/τ" (fieldᵢ …))

  #'(begin
      «define-common»
      (provide (struct-out common-struct))

      (pre-declare-tagged-and-node common-struct name [fieldᵢ …])
      …))

«pre-declare-all-tagged-structure-structs»3 ::=

(define-syntax/case
    (pre-declare-tagged-and-node common-struct name (fieldᵢ …)) ()

  (define-temp-ids "~a/τ" (fieldᵢ …))
  (define-temp-ids "~a/pred" (fieldᵢ …))
  (define/with-syntax ([_ . Anyᵢ] …) #'([fieldᵢ . Any] …))
  (define/with-syntax tagged-struct
    (make-struct-identifier-tagged #f #'(name fieldᵢ …)))
  (define/with-syntax tagged-pred
    (make-struct-identifier-tagged-pred #f #'(name fieldᵢ …)))
  (define/with-syntax node-struct
    (make-struct-identifier-node #f #'(name fieldᵢ …)))

  (template (begin
              «define-tagged»
              «define-tagged-pred»
              «define-node»
              (provide tagged-pred
                       (struct-out tagged-struct)
                       (struct-out node-struct)))))

B.2.6.2 Remembering tagged structures across compilations

In order to know which structs to pre-declare, we need to remember them across compilations. We use the remember library for that purpose.

«all-remembered-tagged-structures» ::=

(set->list (begin (check-adt-context)
(get-remembered 'tagged-structure)))

«remember-structure!» ::=

(remember-write! 'tagged-structure
`(,(syntax-e #'name) . ,sorted-field-symbols))

for-syntax function
(check-remembered-common! #'(name fieldᵢ ...))
for-syntax function
(check-remembered-tagged! #'(name fieldᵢ ...))
for-syntax function
(check-remembered-node! #'(name fieldᵢ ...))

These for-syntax functions check whether a tagged structure with the given name and fields has already been remembered, and return the common, tagged or node struct identifier for that tagged structure. If the tagged structure has not yet been remembered, or if it was remembered for the first time during the current compilation, a delayed error is raised, and the function returns the struct identifier for the not-remembered tagged structure as a fallback, so that the current compilation may proceed as far as possible before the delayed error is triggered. The not-remembered tagged structure has no fields, and is always available.

The delayed error asks the user to re-compile the file, as new items have been remembered. The delayed error will be displayed after the file is expanded, but before it is type checked. If another compilation error happens while compiling the rest of the file, then the delayed error will not be displayed.

for-syntax function
(check-remembered-?! #'(name fieldᵢ ...))

This for-syntax function checks whether a tagged structure with the given name and fields has already been remembered, and returns #t in that case. If the tagged structure has not yet been remembered, or if it was remembered for the first time during the current compilation, a delayed error is raised and the function returns #f.

If the name and set of fields were already remembered, all is fine and we simply generate the corresponding struct identifiers:

«check-remembered!»1 ::=

(define-for-syntax/case-args (check-remembered! (name fieldᵢ …))
  (let* ([sorted-fields (sort-fields #'(fieldᵢ …))]
         [sorted-field-symbols (map syntax-e sorted-fields)])
    (when (check-duplicates sorted-field-symbols)
      (raise-syntax-error 'tagged-structure
                          "Duplicate fields in structure descriptor"
                          #f
                          #f
                          sorted-fields))
    (check-adt-context)
    (if (remembered? 'tagged-structure `(,(syntax-e #'name)
                                         . ,sorted-field-symbols))
        (values
         #t
         (make-struct-identifier-common #t sorted-fields)
         (make-struct-identifier-tagged #t `(,#'name . ,sorted-fields))
         (make-struct-identifier-node #t `(,#'name . ,sorted-fields)))
        «not-remembered»)))

«check-remembered!»2 ::=

(define-for-syntax (check-remembered-common! descriptor)
  (let-values ([(? common tagged node) (check-remembered! descriptor)])
    common))
(define-for-syntax (check-remembered-tagged! descriptor)
  (let-values ([(? common tagged node) (check-remembered! descriptor)])
    tagged))
(define-for-syntax (check-remembered-node! descriptor)
  (let-values ([(? common tagged node) (check-remembered! descriptor)])
    node))
(define-for-syntax (check-remembered-?! descriptor)
  (let-values ([(? common tagged node) (check-remembered! descriptor)])
    ?))

The struct identifiers are generated as shown below. Since their identifier is of the form "(structure field₀ field₁ …)", it contains the unusual characters "(" and ")". This reduces the risk of conflicts between struct identifiers produced by this library and user-declared identifiers (the structs declared by this library normally have a fresh scope, but due to bug #399 this is currently not possible).

«make-struct-identifier-from-list» ::=

(define/contract? (make-struct-identifier-from-list ctx-introduce? lst)
  (-> boolean?
      (listof symbol?)
      identifier?)

  ((if ctx-introduce? ctx-introduce syntax-local-introduce)
   #`#,(string->symbol
        (~a lst))))

«make-struct-identifier-common» ::=

(define/contract? (make-struct-identifier-common ctx-introduce? fields)
  (-> boolean?
      (stx-list/c (listof identifier?))
      identifier?)

  (make-struct-identifier-from-list
   ctx-introduce?
   `(common . ,(map syntax-e (sort-fields fields)))))

«make-struct-identifier-tagged» ::=

(define/contract? (make-struct-identifier-tagged ctx-introduce?
                                                 name+fields)
  (-> boolean?
      (stx-list/c (cons/c identifier? (listof identifier?)))
      identifier?)

  (make-struct-identifier-from-list
   ctx-introduce?
   `(tagged ,(syntax-e (stx-car name+fields))
            . ,(map syntax-e
                    (sort-fields (stx-cdr name+fields))))))

«make-struct-identifier-node» ::=

(define/contract? (make-struct-identifier-node ctx-introduce?
                                               name+fields)
  (-> boolean?
      (stx-list/c (cons/c identifier? (listof identifier?)))
      identifier?)

  (make-struct-identifier-from-list
   ctx-introduce?
   `(node ,(syntax-e (stx-car name+fields))
          . ,(map syntax-e
                  (sort-fields (stx-cdr name+fields))))))

«make-struct-identifier-tagged-pred» ::=

(define/contract?
    (make-struct-identifier-tagged-pred ctx-introduce?
                                        name+fields)
  (-> boolean?
      (stx-list/c (cons/c identifier? (listof identifier?)))
      identifier?)

  (make-struct-identifier-from-list
   ctx-introduce?
   `(tagged-cast-predicate
     ,(syntax-e (stx-car name+fields))
     . ,(map syntax-e
             (sort-fields (stx-cdr name+fields))))))

B.2.6.3 Sorting the set of fields

Some operations will need to obtain the Racket struct for a given set of fields. The fields are first sorted, in order to obtain a canonical specification for the structure.

«sort-fields» ::=

(define/contract? (sort-fields fields)
  (-> (stx-list/c (listof identifier?))
      (listof identifier?))

  (when (check-duplicates (stx->list fields) #:key syntax-e)
    (raise-syntax-error 'tagged-structure
                        "Duplicate fields in structure descriptor"
                        fields))
  (sort (stx->list fields)
        symbol<?
        #:key syntax-e))

The sort-fields-alist function will sort an associative list where the keys are field identifiers. This allows us later to sort a list of fields associated with their type, for example.

«sort-fields-alist» ::=

(define/contract? (sort-fields-alist fields-alist)
  (-> (stx-list/c (listof (stx-car/c identifier?)))
      (listof (stx-e/c (cons/c identifier? any/c))))

  (when (check-duplicates (map (λ~> stx-car stx-e)
                               (stx->list fields-alist)))
    (raise-syntax-error 'structure
                        "Duplicate fields in structure description"
                        (stx-map stx-car fields-alist)))
  (sort (stx->list fields-alist)
        symbol<?
        #:key (λ~> stx-car stx-e)))

B.2.6.4 Not-yet-remembered structs should cause an error

If the set of fields given to check-remember-structure! is not already known, it is remembered (i.e. written to a file by the remember library), so that it will be known during the next compilation. A delayed error is then set up, and a dummy struct identifier is returned (the struct identifier associated with the tagged structure not-remembered, which does not have any field).

«not-remembered» ::=

(begin «remember-structure!»
       (remembered-error! 'tagged-structure
                          #'(name fieldᵢ …)
                          (syntax->list #'(name fieldᵢ …)))
       (values
        #f
        (make-struct-identifier-common #t '())
        (make-struct-identifier-tagged #t `(,#'not-remembered))
        (make-struct-identifier-node #t `(,#'not-remembered))))

The structure with no fields is pre-remembered so that it is always available and can be returned in place of the actual struct when the requested set of fields has not been remembered yet:

«remember-empty-tagged-structure» ::=

(remembered! tagged-structure (not-remembered))

Our goal is to let the file be macro-expanded as much as possible before an error is triggered. That way, if the file contains multiple structures which have not yet been remembered, they can all be remembered in one compilation pass, instead of stumbling on each one in turn.

We use the not-remembered tagged structure as a fallback when a structure is not already remembered. This is semantically incorrect, and obviously would not typecheck, as the user code would expect a different type. However, the delayed error is triggered before the type checker has a chance to run: the type checker runs on the fully-expanded program, and the error is triggered while the program is still being macro-expanded.

The compilation may however fail earlier. For example, if a reflective operation attempts to obtain a struct’s accessor for a given field, but that struct corresponds to a structure which was not yet remembered, then this operation will fail at compile-time. All the primitive operations implemented in this file should however work even if the structure wasn’t remembered, giving results which will not typecheck but can still be expanded.

We additionally always declare a tagged structure with only the “values” field, as it is the base type for all constructors.

«remember-one-constructor» ::=

(remembered! tagged-structure (always-remembered values))

B.2.7 Creating instances of a tagged structure

for-syntax function
(tagged-builder! #'(name [fieldᵢ τᵢ] ...))

name = Identifier

tvarᵢ = Identifier

fieldᵢ = Identifier

τᵢ = Type

This for-syntax function returns the syntax for a builder function for the given tagged structure. The builder function expects one parameter of type τᵢ for each fieldᵢ.

The builder function has the following type:

(→ τᵢ … (tagged name [fieldᵢ τᵢ] …))

where (tagged name [fieldᵢ τᵢ] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ τᵢ] …))

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-builder!» ::=

(define-for-syntax tagged-builder!
  (λ/syntax-case (name [fieldᵢ τᵢ] …) ()
    (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
    (define/with-syntax ([sorted-fieldⱼ . sorted-τⱼ] …)
      (sort-fields-alist #'([fieldᵢ . τᵢ] …)))
    (cond
      ;Can't use (inst st …) on a non-polymorphic type.
      [(stx-null? #'(fieldᵢ …))
       #'st]
      ;Otherwise, re-order
      [else
       #`(λ ([fieldᵢ : τᵢ] …)
           ((inst st sorted-τⱼ …) (delay sorted-fieldⱼ) …))])))

for-syntax function
(tagged-∀-builder! #'((tvarᵢ ...) name [fieldᵢ τᵢ] ...))

name = Identifier

fieldᵢ = Identifier

tvarᵢ = Identifier

τᵢ = Type

This for-syntax function returns the syntax for a polymorphic builder function for the given tagged structure. The polymorphic builder function has the given tvarᵢ type variables. The polymorphic builder function expects one parameter of type τᵢ for each fieldᵢ, where τᵢ can be a regular type or one of the tvarᵢ type variables.

The builder function has the following type:

(∀ (tvarᵢ …) (→ τᵢ … (tagged name [fieldᵢ τᵢ] …)))

where (tagged name [fieldᵢ τᵢ] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ τᵢ] …))

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-∀-builder!» ::=

(define-for-syntax tagged-∀-builder!
  (λ/syntax-case ((tvarᵢ …) name [fieldᵢ τᵢ] …) ()
    (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
    (define/with-syntax ([sorted-fieldⱼ . sorted-τⱼ] …)
      (sort-fields-alist #'([fieldᵢ . τᵢ] …)))
    (cond
      [(stx-null? #'(tvarᵢ …))
       (tagged-builder! #'(name [fieldᵢ τᵢ] …))]
      ;Can't use (inst st …) on a non-polymorphic type.
      [(stx-null? #'(fieldᵢ …))
       #`(λ #:∀ (tvarᵢ …) () (st))]
      ;Otherwise, re-order
      [else
       #`(λ #:∀ (tvarᵢ …) ([fieldᵢ : τᵢ] …)
           ((inst st sorted-τⱼ …) (delay sorted-fieldⱼ) …))])))

for-syntax function
(tagged-infer-builder! #'(name fieldᵢ ...))

name = Identifier

fieldᵢ = Identifier

This for-syntax function returns the syntax for a polymorphic builder function for the given tagged structure. The polymorphic builder function has one type variable for each field. The polymorphic builder function expects one parameter for each fieldᵢ, and infers the type of that field.

The builder function has the following type:

(∀ (τᵢ …) (→ τᵢ … (tagged name [fieldᵢ τᵢ] …)))

where (tagged name [fieldᵢ τᵢ] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ τᵢ] …))

with a fresh τᵢ identifier is introduced for each fieldᵢ.

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-infer-builder!» ::=

(define-for-syntax tagged-infer-builder!
  (λ/syntax-case (name fieldᵢ …) ()
    (define-temp-ids "~a/τ" (fieldᵢ …))
    (tagged-∀-builder! #'((fieldᵢ/τ …) name [fieldᵢ fieldᵢ/τ] …))))

B.2.8 Predicate for a tagged structure

for-syntax function
(tagged-any-predicate! #'(name fieldᵢ ...))

name = Identifier

fieldᵢ = Identifier

This for-syntax function returns the syntax for a predicate for the given tagged structure. No check is performed on the contents of the structure’s fields, i.e. the predicate has the following type:

(→ Any Boolean : (tagged name [fieldᵢ Any] …))

where (tagged name [fieldᵢ Any] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ Any] …))

In other words, it is a function accepting any value, and returning #t if and only if the value is an instance of a structure with the given tag name and fields, regardless of the contents of those fields. Otherwise, #f is returned.

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-any-predicate!» ::=

(define-for-syntax/case-args (tagged-any-predicate! (name fieldᵢ …))
  (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
  (define/with-syntax ([_ . Anyᵢ] …) #'([fieldᵢ . Any] …))
  #'(make-predicate (maybe-apply-type st Anyᵢ …)))

for-syntax function
(tagged-any-fields-predicate #'name)

name = Identifier

This for-syntax function returns the syntax for a predicate for any tagged structure with the given name. No check is performed on the structure’s fields.

«tagged-any-fields» ::=

(define-for-syntax tagged-any-fields
  (λ/syntax-parse tag-name:id
    (map (λ (name+fields)
           (with-syntax ([(name fieldᵢ …) name+fields])
             (cons (check-remembered-tagged! #'(name fieldᵢ …))
                   name+fields)))
         (filter (λ (name+fields) (equal? (car name+fields)
                                          (syntax-e #'tag-name)))
                 «all-remembered-tagged-structures»))))

«tagged-any-fields-predicate» ::=

(define-for-syntax tagged-any-fields-predicate
(λ/syntax-parse tag-name:id
#`(make-predicate #,(tagged-any-fields-type #'tag-name))))

B.2.8.1 A predicate over the contents of the fields

for-syntax function
(tagged-predicate! #'(name [fieldᵢ τᵢ] ...))

name = Identifier

fieldᵢ = Identifier

τᵢ = Type

This for-syntax function returns the syntax for a predicate for the given tagged structure. The predicate also checks that each fieldᵢ is a value of the corresponding τᵢ type. Each given τᵢ must be a suitable argument for Typed Racket’s make-predicate.

The predicate has the following type:

(→ Any Boolean : (tagged name [fieldᵢ τᵢ] …))

where (tagged name [fieldᵢ τᵢ] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ τᵢ] …))

In other words, it is a function accepting any value, and returning #t if and only if the value is an instance of a structure with the given tag and fields, and each fieldᵢ contains a value of the type τᵢ. Otherwise, #f is returned. Note that the actual values contained within the fields are checked, instead of their static type (supplied or inferred when building the tagged structure instance).

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!.

Typed Racket’s make-predicate cannot operate on promises, because its automatic contract generation would need to force the promise. This is a potentially side-effectful operation that a predicate should not perform automatically. In our case, we know that by construction the promises are side effect-free. We therefore manually define a predicate builder. The returned predicate forces the promises contained within each fieldᵢ, and checks whether the resulting value is of the corresponding type τᵢ:

«tagged-pred-lambda» ::=

(λ (fieldᵢ/pred …)
  (λ ([v : Any])
    (and ((struct-predicate tagged-struct) v)
         (fieldᵢ/pred (force ((struct-accessor common-struct fieldᵢ) v)))
         …)))

Unfortunately, Typed Racket’s inference is not strong enough to properly express the type of the predicate we build above; as of the time of writing this library, it infers that when the predicate returns #true, v has the (tagged-struct Anyᵢ …) type, and that its fields have the respective fieldᵢ/τ type. It also infers that when the predicate returns false, one of these propositions must be falseThese negative propositions cannot be written with the syntax currently supported by Typed Racket, but they are still shown by Typed Racket for debugging purposes in error messages, for example when trying to annotate the function with an incorrect proposition.. However, it is not currently capable of combining these pieces of information into a single proposition asserting that the type of v is (tagged-struct fieldᵢ/τ …) if and only if the predicate returns true. To circumvent this precision problem, we annotate the predicate builder defined above with the most precise type that can be expressed and automatically validated by Typed Racket:

«tagged-pred-simple-type» ::=

(∀ (fieldᵢ/τ …)
   (→ (→ Any Boolean : fieldᵢ/τ)
      …
      (→ Any Boolean : #:+ (!maybe-apply tagged-struct Anyᵢ …))))

We then use unsafe-castIt would be tempting to use the safe cast, but cast enforces the type with a contract, which, in this case, cannot be generated by the current version of Typed Racket. to give the predicate the more precise type:

«tagged-pred-correct-type» ::=

(∀ (fieldᵢ/τ …)
   (→ (→ Any Any : fieldᵢ/τ)
      …
      (→ Any Boolean : (!maybe-apply tagged-struct fieldᵢ/τ …))))

«define-tagged-pred» ::=

(define tagged-pred
  (unsafe-cast/no-expand (ann «tagged-pred-lambda»
                              «tagged-pred-simple-type»)
                         «tagged-pred-correct-type»))

Finally, we can define the tagged-predicate! for-syntax function described earlier in terms of this specialised predicate builder.

«tagged-predicate!» ::=

(define-for-syntax/case-args (tagged-predicate! (name [fieldᵢ τᵢ] …))
  (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
  (define/with-syntax ([sorted-fieldⱼ . sorted-τⱼ] …)
    (sort-fields-alist #'([fieldᵢ . τᵢ] …)))
  (define/with-syntax st-make-predicate
    (make-struct-identifier-tagged-pred #t #'(name fieldᵢ …)))
  #'(st-make-predicate (make-predicate sorted-τⱼ) …))

for-syntax function
(tagged-pred-predicate! #'(name [fieldᵢ predᵢ] ...))

name = Identifier

fieldᵢ = Identifier

predᵢ = (ExpressionOf (→ Any Any : τᵢ))

This for-syntax function returns the syntax for a predicate for the given tagged structure. The predicate also checks that each fieldᵢ is accepted by the corresponding predicate predᵢ.

When the type of a given predᵢ includes a filter : τᵢ asserting that it returns true if and only if the value is of type τᵢ, then the predicate produced by tagged-predicate! will also have that filter on the corresponding field. By default, a function of type (→ Any Any) will implicitly have the Any filter, which does not bring any extra information. In other words, the (→ Any Any) type in which no filter is specified is equivalent to the (→ Any Any : Any) type, where : Any indicates the filter.

The generated predicate has therefore the following type:

(→ Any Boolean : (tagged name [fieldᵢ τᵢ] …))

where (tagged name [fieldᵢ τᵢ] …) is the type produced by:

(tagged-type! #'(name [fieldᵢ τᵢ] …))

This function also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!.

«tagged-pred-predicate!» ::=

(define-for-syntax/case-args
    (tagged-pred-predicate! (name [fieldᵢ predᵢ] …))
  (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
  (define/with-syntax ([sorted-fieldⱼ . sorted-predⱼ] …)
    (sort-fields-alist #'([fieldᵢ . predᵢ] …)))
  (define/with-syntax st-make-predicate
    (make-struct-identifier-tagged-pred #t #'(name fieldᵢ …)))
  #'(st-make-predicate sorted-predⱼ …))

B.2.9 Matching against tagged structures

for-syntax function
(tagged-match! #'(name [fieldᵢ patᵢ] ...))

name = Identifier

fieldᵢ = Identifier

patᵢ = Match-Pattern

This for-syntax function returns the syntax for a match pattern for the given tagged structure. The pattern matches each fieldᵢ against the corresponding patᵢ. It also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-match!» ::=

(define-for-syntax/case-args (tagged-match! (name [fieldᵢ patᵢ] …))
  (define-values (was-remembered common-struct tagged-struct node-struct)
    (check-remembered! #'(name fieldᵢ …)))
  (define/with-syntax st tagged-struct)
  (define/with-syntax ([sorted-fieldⱼ . sorted-patⱼ] …)
    (sort-fields-alist #'([fieldᵢ . patᵢ] …)))
  (if was-remembered
      #'(struct st ((app force sorted-patⱼ) …))
      «match-not-remembered»))

The match pattern (struct st (pat …)) fails to compile when the struct st is not declared, and when it does not have the right number of fields. To avoid a confusing error message when the tagged structure was not remembered yet, we insert a dummy pattern but still process the nested patterns. This way, the nested patterns can themselves raise not-remembered errors and cause new tagged structures to be remembered.

«match-not-remembered» ::=

#'(app (λ (v) 'not-remembered) (and sorted-patⱼ …))

for-syntax function
(tagged-anytag-match! #'([fieldᵢ patᵢ] ...))

fieldᵢ = Identifier

patᵢ = Match-Pattern

This for-syntax function returns the syntax for a match pattern for any tagged structure with the given fields, regardless of the tagged structure’s tag. The pattern matches each fieldᵢ against the corresponding patᵢ. It also checks that a tag with a dummy name (any-tag) and the given fields has already been remembered, using check-remembered-tagged!

«tagged-anytag-match!» ::=

(define-for-syntax/case-args (tagged-anytag-match! ([fieldᵢ patᵢ] …))
  (define-values (was-remembered common-struct tagged-struct node-struct)
    (check-remembered-tagged! #'(any-tag fieldᵢ …)))
  (define/with-syntax st common-struct)
  (define/with-syntax ([sorted-fieldⱼ . sorted-patⱼ] …)
    (sort-fields-alist #'([fieldᵢ . patᵢ] …)))
  (if was-remembered
      #'(struct st ((app force sorted-patⱼ) …))
      «match-not-remembered»))

B.2.10 Type of a tagged structure

for-syntax function
(tagged-type! #'(name [fieldᵢ τᵢ] ...))

name = Identifier

fieldᵢ = Identifier

This for-syntax function returns the syntax for the type of tagged structures with the given name and field types. It also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-type!» ::=

(define-for-syntax tagged-type!
  (λ/syntax-case (name [fieldᵢ τᵢ] …) ()
    (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
    (define/with-syntax ([sorted-fieldⱼ . sorted-τⱼ] …)
      (sort-fields-alist #'([fieldᵢ . τᵢ] …)))
    ;Can't instantiate a non-polymorphic type.
    (if (stx-null? #'(fieldᵢ …))
        #'st
        #'(st sorted-τⱼ …))))

for-syntax function
(tagged-∀-type! #'((tvarᵢ ...) name [fieldᵢ τᵢ] ...))

name = Identifier

fieldᵢ = Identifier

This for-syntax function returns the syntax for a polymorphic type for the given tagged structure, using the given type variables tvarᵢ…. It also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-∀-type!» ::=

(define-for-syntax tagged-∀-type!
  (λ/syntax-case ((tvarᵢ …) name [fieldᵢ τᵢ] …) ()
    (define/with-syntax st (check-remembered-tagged! #'(name fieldᵢ …)))
    (define/with-syntax ([sorted-fieldⱼ . sorted-τⱼ] …)
      (sort-fields-alist #'([fieldᵢ . τᵢ] …)))
    (cond
      [(stx-null? #'(tvarᵢ …))
       (tagged-type! #'(name [fieldᵢ τᵢ] …))]
      ;Can't instantiate a non-polymorphic type.
      [(stx-null? #'(fieldᵢ …))
       #`(∀ (tvarᵢ …) st)]
      ;Otherwise, re-order
      [else
       #`(∀ (tvarᵢ …) (st sorted-τⱼ …))])))

for-syntax function
(tagged-infer-type! #'(name fieldᵢ ...))

name = Identifier

fieldᵢ = Identifier

This for-syntax function returns the syntax for a polymorphic type for the given tagged structure, with one automatically-generated type variable per field. It also checks that a tag with the given name and fields has already been remembered, using check-remembered-tagged!

«tagged-infer-type!» ::=

(define-for-syntax tagged-infer-type!
  (λ/syntax-case (name fieldᵢ …) ()
    (define-temp-ids "~a/τ" (fieldᵢ …))
    (tagged-∀-type! #'((fieldᵢ/τ …) name [fieldᵢ fieldᵢ/τ] …))))

for-syntax function
(tagged-any-fields-type #'name)

name = Identifier

This for-syntax function returns the syntax for the union type of all tagged structures with the given name. The type of each field is Any.

«tagged-any-fields-type» ::=

(define-for-syntax tagged-any-fields-type
  (λ/syntax-parse tag-name:id
    (define/with-syntax ([sᵢ nameᵢ fieldᵢⱼ …] …)
      (tagged-any-fields #'tag-name))
    (define/with-syntax ([[_ Anyᵢⱼ] …] …)
      #'([[fieldᵢⱼ Any] …] …))
    #`(U . #,(stx-map (λ (sᵢ Anyᵢⱼ*) (if (stx-null? Anyᵢⱼ*)
                                         sᵢ
                                         #`(#,sᵢ . #,Anyᵢⱼ*)))
                      #'(sᵢ …)
                      #'([Anyᵢⱼ …] …)))))

B.2.11 Accessing fields of tagged structures

syntax
(tagged-get-field v f)

Returns the value contained within the f field of the tagged structure instance v.

«tagged-get-field» ::=

(define-syntax (tagged-get-field stx)
  (syntax-case stx ()
    [(_ v f . else-expr)
     (identifier? #'f)
     (let ()
       (define/with-syntax else-expr-or-error
         (syntax-case #'else-expr ()
           [() (if (identifier? #'v)
                   #`(typecheck-fail #,stx #:covered-id v)
                   #`(typecheck-fail #,stx))]
           [(e) #'e]))
       (define/with-syntax ([sⱼ all-fieldⱼₖ …] …)
         (has-fields/common #'(f)))
       #'(let ([v-cache v])
           (cond
             [((struct-predicate sⱼ) v-cache)
              (force ((struct-accessor sⱼ f) v))]
             …
             [else else-expr-or-error])))]))

syntax
(λ-tagged-get-field f)

Returns an accessor for the f field of any tagged structure instance. The instance must contain a field named f, otherwise a type error is raised at compile-time, when using the accessor on an inappropriate value.

«λ-tagged-get-field» ::=

(define-syntax/parse (λ-tagged-get-field f:id)
  (define/with-syntax ([sⱼ all-fieldⱼₖ …] …)
    (has-fields/common #'(f)))
  #`(λ #:∀ (τ) ([v : #,(has-fields/type #'([f τ]))])
      (cond [((struct-predicate sⱼ) v)
             (force ((struct-accessor sⱼ f) v))]
            …)))

B.2.12 Row polymorphism

Row polymorphism, also known as "static duck typing" is a type system feature which allows a single type variable to be used as a place holder for several omitted fields, along with their types. The phc-adt library supports a limited form of row polymorphism: for most operations, a set of tuples of omitted field names must be specified, thereby indicating a bound on the row type variable.

This is both an limitation of our implementation (to reduce the combinatorial explosion of possible input and output types), as well as a desirable feature. Indeed, this library is intended to be used to write compilers, and a compiler pass should have a precise knowledge of the intermediate representation it manipulates. It is possible that a compiler pass may operate on several similar intermediate representations (for example a full-blown representation for actual compilation and a minimal representation for testing purposes), which makes row polymorphism desirable. It is however risky to allow as an input to a compiler pass any data structure containing at least the minimum set of required fields: changes in the intermediate representation may add new fields which should, semantically, be handled by the compiler pass. A catch-all row type variable would simply ignore the extra fields, without raising an error. Thanks to the bound which specifies the possible tuples of omitted field names, changes to the the input type will raise a type error, bringing the programmer’s attention to the issue. If the new type is legit, and does not warrant a modification of the pass, the fix is easy to implement: simply adding a new tuple of possibly omitted fields to the bound (or replacing an existing tuple) will allow the pass to work with the new type. If, on the other hand, the pass needs to be modified, the type system will have successfully caught a potential issue.

This section presents the implementation of the features which allow a limited form of row polymorphism, as well as structural subtyping.

B.2.12.1 Type for any tagged structure containing a given set of fields

for-syntax function
(has-fields stx-fields)
→
(listof (cons/c identifier?
                (cons/c identifier?
                        (listof identifier?))))
  stx-fields : (syntax/c (listof identifier?))

Returns a list of tagged structures which have all of the given fields. Each tagged structure list with the low-level struct’s id as the first element, the tag name as the second element, followed by the whole list of fields which belong to that tagged structure.

«has-fields»1 ::=

(define-for-syntax has-fields
  (λ/syntax-case (fieldᵢ …) ()
    (map (λ (t+fields)
           (with-syntax ([(tag fieldᵢ …) t+fields])
             (list* (make-struct-identifier-common #t #'(fieldᵢ …))
                    #'tag
                    (sort-fields #'(fieldᵢ …)))))
         (filter (λ (s)
                   (andmap (λ (f) (member f (cdr s)))
                           (syntax->datum #'(fieldᵢ …))))
                 «all-remembered-tagged-structures»))))

for-syntax function
(has-fields/common #'(fieldᵢ ...))

Returns a list of “common” structs which have all of the given fields. Each “common” struct is represented as a pair of the struct’s id and the whole list of fields which belong to that tagged structure.

«has-fields»2 ::=

(define-for-syntax (has-fields/common stx-fields)
  (remove-duplicates (map (λ (s) (cons (car s) (cddr s)))
                          (has-fields stx-fields))
                     free-identifier=?
                     #:key car))

for-syntax function
(has-fields/type #'([fieldᵢ τᵢ] ...))

Returns the syntax for the union type of several “common” structs. Each tagged structure has all of the given fields, and each fieldᵢ is of the corresponding type τᵢ. The other extra fields which are not part of the #'([fieldᵢ τᵢ] …) specification have the Any type.

«has-fields/type» ::=

(define-for-syntax has-fields/type
  (λ/syntax-case ([fieldᵢ τᵢ] …) ()
    (define/with-syntax ((sⱼ all-fieldⱼₖ …) …)
      (has-fields/common #'(fieldᵢ …)))
    (define/with-syntax ((all-field-τⱼₖ …) …)
      (template
       ([(!cdr-assoc #:default Any all-fieldⱼₖ [fieldᵢ . τᵢ] …) …] …)))
    #'(U (maybe-apply-type sⱼ all-field-τⱼₖ …) …)))

B.2.12.2 Changing the tag of a tagged structure

syntax
(change-tag instance [(tagᵢ fieldᵢⱼ ...) new-tagᵢ] ...)

The change-tag macro takes an instance of a tagged structure, and produces a new tagged structure instance with a different tag name. The instance’s type must be one of (tagged tagᵢ fieldᵢⱼ …) …. The new instance will contain the same fields as the original, but its tag name will be the new-tagᵢ corresponding to the input’s type.

«change-tag» ::=

(define-syntax/case (change-tag [(tagᵢ fieldᵢⱼ …) new-tagᵢ] …)
  «change-tag-factored-out»
  #`(cond #,(stx-map «change-tag-case»
                     #'([tagᵢ (fieldᵢⱼ …) new-tagᵢ]))))

«change-tag-factored-out» ::=

(define old-s (check-remembered-tagged! #'(tag fieldⱼₛ)))

«change-tag-case» ::=

(λ/syntax-case (tag (fieldⱼ …) new-tag) ()
  (define/with-syntax (fieldⱼₛ …) (sort-fields #'(fieldⱼ …)))
  (define new-s (check-remembered-tagged! #'(new-tag fieldⱼₛ)))
  #'[((struct-predicate old-s) instance)
     ((struct-constructor new-s)
      ((struct-accessor new-s fieldⱼₛ) instance) …)])

B.2.12.3 Splitting a tagged structure

syntax
(split instance : (U (tagᵢ fieldᵢⱼ ...) ...) requestedₖ ...)

The split macro splits a tagged structure into two tagged structures. The first contains the requestedₖ … fields, while the second contains all other fields. The two new tagged structures have the same tag as the original instance. This can however be altered later on using change-tag.

The expression generated by split produces two values, one for each new tagged structure.

Since the type of the instance is not known at compile-time, this form requires that the user specify a union of possible tagged structure types. In theory, it would be possible to use the list of all tagged structures, but this would result in a cond testing over a large number of impossible cases.

The trivial library could help by tracking the type of expressions in simple cases. That information could then be used to infer the list of possible tagged structures. The explicit annotation would then become mandatory only when the type could not be inferred.

The split macro generates a cond form, with one clause for each possible instance type. In each cond clause, the requestedₖ … and the other fields are separated into two different tagged structures, the first .

«split»1 ::=

(define-syntax split
  (syntax-parser
    #:literals (U)
    [(_ instance :colon (U (~and τᵢ (tagᵢ fieldᵢⱼ …)) …) requestedₖ …)
     «split-check»
     «split-compute-extra-fields»
     «split-case-factored-out»
     #`(cond
         #,@(stx-map «split-case» #'([tagᵢ (extra-fieldᵢₗ …)] …)))]))

The split macro first computes the set of extra fields for each possible input type:

«split-compute-extra-fields» ::=

(define/with-syntax ((extra-fieldᵢₗ …) …)
  (stx-map (λ (x)
             (free-id-set->list
              (free-id-set-subtract x requested-id-set)))
           instance-id-sets))

It then generates a cond clause for each possible input type, which tests whether the instance belongs to that type. If it is the case, then the body of the clause

«split-case-factored-out» ::=

(define/with-syntax (requestedₖₛ …) (sort-fields #'(requestedₖ …)))

«split-case» ::=

(λ/syntax-case (tag (extraₗ …)) ()
  (define/with-syntax (extraₗₛ …) (sort-fields #'(extraₗ …)))
  (define/with-syntax s-requested (check-remembered-tagged! #'(tag requestedₖ …)))
  (define/with-syntax s (check-remembered-tagged! #'(tag requestedₖ … extraₗ …)))
  (define/with-syntax c (check-remembered-common! #'(tag requestedₖ … extraₗ …)))
  (define/with-syntax s-extra (check-remembered-tagged! #'(tag extraₗ …)))
  ;the generated cond clause:
  #'[((struct-predicate s) instance)
     (values ((struct-constructor s-requested)
              ((struct-accessor c requestedₖₛ) instance) …)
             ((struct-constructor s-extra)
              ((struct-accessor c extraₗₛ) instance) …))])

The argument-verification code for split is given below. It uses immutable-free-id-sets to quickly compute the set of identifiers present within requestedₖ … but missing from one of the fieldᵢⱼ … tuples.

«split-check» ::=

(define instance-id-sets
  (stx-map (∘ immutable-free-id-set syntax->list) #'((fieldᵢⱼ …) …)))

(define requested-id-set
  (immutable-free-id-set (syntax->list #'(requestedₖ …))))

(for ([τ (in-syntax #'(τᵢ …))]
      [instance-id-set instance-id-sets])
  (let ([missing (free-id-set-subtract requested-id-set
                                       instance-id-set)])
    (unless (free-id-set-empty? missing)
      «split-error»)))

If there are such missing identifiers, the macro raises an error, otherwise the computation proceeds normally:

«split-error» ::=

(raise-syntax-error
'split
(format "The requested fields ~a are missing from the instance type ~a"
(free-id-set->list missing)
τ)
this-syntax
τ
(free-id-set->list missing))

syntax
(split/type #'((U (tagᵢ [fieldᵢⱼ τᵢⱼ] ...) ...) requestedₖ ...))

We also define a split/type for-syntax function, which returns the syntax for the union type of the extra fields of a split operation, i.e. the type of the second value produced by split.

«split»2 ::=

(define-for-syntax split/type
  (syntax-parser
    #:literals (U)
    [((U {~and τᵢ (tagᵢ [fieldᵢⱼ τᵢⱼ] …)} …) requestedₖ …)
     «split-check»
     (define/with-syntax (([extra-fieldᵢₗ . extra-τᵢₗ] …) …)
       (for/list ([field+τⱼ… (in-syntax #'(([fieldᵢⱼ . τᵢⱼ] …) …))])
         (~for/list ([($stx [field . τ]) (in-syntax field+τⱼ…)]
                     #:unless (free-id-set-member? requested-id-set
                                                   #'field))
                    #'[field . τ])))
     #`(U #,@(stx-map tagged-type! #'([tagᵢ (extra-fieldᵢₗ …)] …)))]))

B.2.12.4 Merging two tagged structures

syntax
(merge instance-a instance-b
: (U [(tag-aᵢ field-aᵢⱼ ...) (tag-bₖ field-bₖₗ ...)] ...))

The merge macro merges two tagged structures into a single one. The resulting structure will contain all the fields field1ᵢⱼ … field2ₖₗ …, and will have the same tag as instance1 (although the tag can be changed later on using change-tag).

Since the type of instance1 and instance2 is not known at compile-time, this form requires that the user specify a union of possible tagged structure types for both instances. In theory, it would be possible to use the list of all tagged structures, but the resulting cond would test for each possible pair of tagged structure types. In other words, the number of pairs of types to account for would be the Cartesian product of all tagged structures used in the program. Clearly, this is not a viable solution.

If the trivial library were to be used, node types should be excluded. Indeed, the node types rely on the fact that they cannot be constructed outside of a graph to provide useful guarantees (e.g. the possibility to map over all nodes of a given type contained within a graph).

«merge»1 ::=

(define-syntax merge
  (syntax-parser
    #:literals (U)
    [(_ instance-a instance-b
        :colon [U [(~and τ-a (tag-aᵢ field-aᵢⱼ …))
                   (~and τ-b (tag-bₖ field-bₖₗ …))] …])
     #`(cond
         #,@(stx-map «merge-case» #'([(τ-a tag-aᵢ field-aᵢⱼ …)
                                      (τ-b tag-bₖ field-bₖₗ …)]
                                     …)))]))

«merge-case» ::=

(λ/syntax-case [(τ-a tag-a field-aⱼ …) (τ-b tag-b field-bₗ …)] ()
  «merge-check»
  (define/with-syntax s-a (check-remembered-tagged! #'(tag-a field-aⱼ …)))
  (define/with-syntax c-a (check-remembered-common! #'(tag-a field-aⱼ …)))
  (define/with-syntax s-b (check-remembered-tagged! #'(tag-b field-bₗ …)))
  (define/with-syntax c-b (check-remembered-common! #'(tag-b field-bₗ …)))
  (define/with-syntax (field-aⱼₛ …) (sort-fields #'(field-aⱼ …)))
  (define/with-syntax (field-bₗₛ …) (sort-fields #'(field-bₗ …)))
  (define s-new (check-remembered-tagged!
                 #'(tag-a field-aⱼₛ … field-bₗₛ …)))
  #`[(and ((struct-predicate s-a) instance-a)
          ((struct-predicate s-b) instance-b))
     (#,(tagged-infer-builder! #'(tag-a field-aⱼₛ … field-bₗₛ …))
      (force ((struct-accessor c-a field-aⱼₛ) instance-a))
      …
      (force ((struct-accessor c-b field-bₗₛ) instance-b))
      …)])

«merge-check» ::=

(define fields-a-id-set
  (immutable-free-id-set (syntax->list #'(field-aⱼ …))))
(define fields-b-id-set
  (immutable-free-id-set (syntax->list #'(field-bₗ …))))
(let ([intersection (free-id-set-intersect fields-a-id-set
                                           fields-b-id-set)])
  (unless (free-id-set-empty? intersection)
    «merge-error»))

«merge-error» ::=

(raise-syntax-error
'merge
(format "The fields ~a are present in both tagged structures ~a and ~a"
         (free-id-set->list intersection)
         #'τ-a
         #'τ-b)
this-syntax
#'τ-a
(free-id-set->list intersection))

syntax
(merge/type #'(U [(tag-aᵢ [field-aᵢⱼ τ-aᵢⱼ] ...)
(tag-bᵢ [field-bᵢⱼ τ-bᵢⱼ] ...)] ...))

We also define a merge/type for-syntax function, which returns the syntax for the union type of the extra fields of a split operation, i.e. the type of the second value produced by split.

«merge»2 ::=

(define-for-syntax merge/type
  (syntax-parser
    #:literals (U)
    [(U [(~and τ-a (tag-aᵢ field-aᵢⱼ …))
         (~and τ-b (tag-bₖ field-bₖₗ …))] …)
     #`(U #,@(stx-map «merge-type-case»
                      #'([tag-aᵢ field-aᵢⱼ … field-bₖₗ …] …)))]))

«merge-type-case» ::=

(λ/syntax-case [(τ-a tag-a field-aⱼ …) (τ-b tag-b field-bₗ …)] ()
«merge-check»
(tagged-type! #'[tag-a field-aⱼ … field-bₗ …]))

B.2.12.5 Updating a tagged structure

syntax
(with+ instance : (U (tagᵢ fieldᵢⱼ ...) ...)
[new-field value] ...)

The with+ macro produces a tagged structure instance containing the same fields as instance, extended with the given new-fields. None of the new-field … must be present in the original instance.

Since the type of the instance is not known at compile-time, this form requires that the user specify a union of possible tagged structure types for the instance. In theory, it would be possible to use the list of all tagged structures, but the resulting cond would test for a large number of impossible cases.

«with+» ::=

(define-syntax/parse (with+ instance
                           :colon (U {~and τᵢ (tagᵢ fieldᵢⱼ …)} …)
                           [new-fieldₖ valueₖ] …)
  «with+-check»
  #'(with! instance : (U (tagᵢ fieldᵢⱼ …) …) [new-fieldₖ valueₖ] …))

«with+-check» ::=

(define instance-id-sets
  (stx-map (∘ immutable-free-id-set syntax->list) #'([fieldᵢⱼ …] …)))
(define new-fields-id-set
  (immutable-free-id-set (syntax->list #'(new-fieldₖ …))))
(for ([τ (in-syntax #'(τᵢ …))]
      [instance-id-set instance-id-sets])
  (let ([intersection (free-id-set-intersect new-fields-id-set
                                             instance-id-set)])
    (unless (free-id-set-empty? intersection)
      «with+-error»)))

«with+-error» ::=

(raise-syntax-error
'with+
(format "The new fields ~a are already present in the instance type ~a"
(map syntax->datum (free-id-set->list intersection))
(syntax->datum τ))
this-syntax
τ
(free-id-set->list intersection))

syntax
(with! instance : (U (tagᵢ fieldᵢⱼ ...) ...)
[updated-field value] ...)

Like with+, but this version allows overwriting fields, i.e. the updated-fields may already be present in the instance. Although the ! is traditionally used in Racket to indicate operations which mutate data structures, in this case it merely indicates that the given fields may exist in the original instance. Since a fresh updated copy of the original instance is created, this operation is still pure.

The same restrictions concerning nodes apply.

«with!» ::=

(define-syntax with!
  (syntax-parser
    #:literals (U)
    [(_ instance :colon (U (tagᵢ fieldᵢⱼ …) …) [updated-fieldₖ valueₖ] …)
     #`(cond
         #,@(stx-map «with!-case» #'([tagᵢ fieldᵢⱼ …] …)))]))

«with!-case» ::=

(λ/syntax-case (tag fieldⱼ …) ()
  (define/with-syntax old-s (check-remembered-tagged! #'(tag fieldⱼ …)))
  (define/with-syntax old-c (check-remembered-common! #'(tag fieldⱼ …)))
  (define field→value
    (make-free-id-table
     (stx-map syntax-e «with!-fieldⱼ-assoc»)))
  «with!-fieldⱼ-overwritten»
  (define/with-syntax ([fieldₗ . maybe-overwrittenₗ] …)
    (free-id-table-map field→value cons))
  #`[((struct-predicate old-s) instance)
     (#,(tagged-infer-builder! #'(tag fieldₗ …)) maybe-overwrittenₗ …)])

The implementation works by initially mapping every fieldⱼ identifier to its value in the original instance:

«with!-fieldⱼ-assoc» ::=

#'([fieldⱼ . (force ((struct-accessor old-c fieldⱼ) instance))] …)

The entries corresponding to an updated-fieldₖ are then overwritten in the table:

«with!-fieldⱼ-overwritten» ::=

(for ([updated-field (in-syntax #'(updated-fieldₖ …))]
[value (in-syntax #'(valueₖ …))])
(free-id-table-set! field→value updated-field value))

syntax
(with!! instance : (U (tagᵢ fieldᵢⱼ ...) ...)
[updated-field value] ...)

Like with!, but checks that all the given fields are already present in the original instance. In other words, it does not change the type of the instance, and merely performs a functional update of the given fields. This version works on a much smaller set of types (namely those containing all the given fields), so the annotation is optional.

The same restrictions concerning nodes apply.

«with!!» ::=

(define-syntax with!!
  (syntax-parser
    ;Auto-detect the set of tagged structures containing
    ;all the updated fields.
    [(_ instance
        [updated-fieldₖ valueₖ] …)
     #:with ([sᵢ tagᵢ fieldᵢⱼ …] …) (has-fields #'(updated-fieldₖ …))
     #'(with! instance : (U (tagᵢ fieldᵢⱼ …) …)
              [updated-fieldₖ valueₖ] …)]
    ;Use an explicit list of tagged structures containing
    ;all the updated fields.
    [(_ instance :colon (U {~and τᵢ (tagᵢ fieldᵢⱼ …)} …)
        [updated-fieldₖ valueₖ] …)
     «with!!-check»
     #'(with! instance : (U (tagᵢ fieldᵢⱼ …) …)
              [updated-fieldₖ valueₖ] …)]))

«with!!-check» ::=

(define instance-id-sets
  (stx-map (∘ immutable-free-id-set syntax->list) #'([fieldᵢⱼ …] …)))
(define updated-id-set
  (immutable-free-id-set (syntax->list #'(updated-fieldₖ …))))
(for ([instance-id-set instance-id-sets]
      [τ (in-syntax #'(τᵢ …))])
  (let ([missing (free-id-set-subtract updated-id-set
                                       instance-id-set)])
    (unless (free-id-set-empty? missing)
      «with!!-error»)))

«with!!-error» ::=

(raise-syntax-error
'with!!
(format "The updated fields ~a are not present in the instance type ~a"
(map syntax->datum (free-id-set->list missing))
(syntax->datum τ))
this-syntax
τ
(free-id-set->list missing))

for-syntax function
(tagged-struct-id? id)
→
(or/c #f
      (cons/c (or/c 'tagged 'node)
              (cons/c identifier
                      (listof identifier))))
  id : any/c

The tagged-struct-id? expects an identifier. When the id is an identifier which refers to a struct definition corresponding to a tagged structure, tagged-struct-id? returns a list containing the tagged structure’s tag name and fields, prefixed with either 'tagged or 'node, depending on whether the given struct id corresponds to a tagged structure’s struct, or to a node’s struct. Otherwise, tagged-struct-id? returns #false.

This can be used to recognise occurrences of tagged structures within fully-expanded types.

«tagged-struct-id?» ::=

(define-for-syntax tagged-struct-ids-cache #f)
(define-for-syntax (tagged-struct-id? id)
  «tagged-struct-ids-init-cache»
  (and (identifier? id)
       (free-id-table-ref tagged-struct-ids-cache id #f)))

The tagged-struct-id function uses a free-identifier table which associates struct identifiers to their corresponding tag name and fields (prefixed with 'tagged or 'node). The table is initialised when tagged-struct-id? is called for the first time. It could not be initialised beforehand, as the adt-init macro needs to be called by the user code first.

«tagged-struct-ids-init-cache» ::=

(unless tagged-struct-ids-cache
  (set! tagged-struct-ids-cache
        (make-immutable-free-id-table
         (append-map (λ (s)
                       (list (list* (make-struct-identifier-tagged #t s)
                                    'tagged
                                    s)
                             (list* (make-struct-identifier-node #t s)
                                    'node
                                    s)))
                     «all-remembered-tagged-structures»))))

B.2.13 Putting it all together

The low-level implementation of algebraic data types is split into three modules: sorting-and-identifiers, pre-declare and the main module. Furthermore, the section Implementation of nodes: printing and equality, implemented as a separate file, contains the implementation details for printing and comparing nodes.

«*» ::=

«module-sorting-and-identifiers»
«module-pre-declare»
«main-module»

The sorting-and-identifiers module contains the utility functions related to sorting fields (to obtain a canonical representation of the tagged structure descriptor), and the functions which derive the struct identifiers for tagged structures, nodes and the “common” supertype of all tagged structures which share the same set of fields. These struct identifiers are derived from the list of field names and the tag name.

«module-sorting-and-identifiers» ::=

(module sorting-and-identifiers racket/base
  (require racket/list
           racket/format
           racket/contract
           phc-toolkit/untyped
           (for-template "ctx.hl.rkt"))

  (provide make-struct-identifier-common
           make-struct-identifier-tagged
           make-struct-identifier-node
           make-struct-identifier-tagged-pred
           sort-fields
           sort-fields-alist)

  «sort-fields»
  «sort-fields-alist»
  «make-struct-identifier-from-list»
  «make-struct-identifier-common»
  «make-struct-identifier-tagged»
  «make-struct-identifier-node»
  «make-struct-identifier-tagged-pred»)

The pre-declare submodule contains everything which concerns the pre-declaration of structs. It also uses the printer and comparer for nodes from Implementation of nodes: printing and equality.

«module-pre-declare» ::=

(module pre-declare typed/racket/base
  (require racket/promise
           racket/string
           racket/require
           phc-toolkit
           remember
           typed-struct-props
           "node-low-level.hl.rkt"
           "ctx.hl.rkt"
           (only-in type-expander unsafe-cast/no-expand)
           (for-syntax racket/base
                       racket/syntax
                       racket/list
                       racket/set
                       racket/function
                       (subtract-in syntax/stx phc-toolkit/untyped)
                       syntax/parse
                       syntax/parse/experimental/template
                       syntax/strip-context
                       phc-toolkit/untyped))
  (require (for-syntax (submod ".." sorting-and-identifiers)))

  (provide (struct-out TaggedTop-struct)
           pre-declare-all-tagged-structure-structs
           pre-declare-group)

  (begin-for-syntax
    (define-template-metafunction !maybe-apply
      (λ (stx)
        (syntax-case stx ()
          [(_ t) #'t]
          [(_ t . args) #'(t . args)]))))

  «remember-empty-tagged-structure»
  «remember-one-constructor»
  «TaggedTop»
  «custom-write»
  «equal+hash»
  «pre-declare-all-tagged-structure-structs»)

The main module contains all the code related to remembering the tagged structures across compilations. It also contains many for-syntax functions which, given the tag name and fields of a tagged structure, produce syntax for that tagged structure’s builder function, type, predicate and match pattern.

«main-module» ::=

(require phc-toolkit
         remember
         racket/promise
         (submod "." pre-declare)
         type-expander
         "ctx.hl.rkt"
         (for-syntax racket/base
                     racket/syntax
                     racket/list
                     racket/set
                     racket/function
                     phc-toolkit/untyped
                     syntax/parse
                     syntax/parse/experimental/template
                     syntax/id-set
                     syntax/id-table
                     generic-bind
                     (submod "." sorting-and-identifiers)))

(provide (for-syntax tagged-builder!
                     tagged-∀-builder!
                     tagged-infer-builder!
                     tagged-type!
                     tagged-∀-type!
                     tagged-infer-type!
                     tagged-predicate!
                     tagged-pred-predicate!
                     tagged-any-predicate!
                     tagged-match!
                     tagged-anytag-match!
                     check-remembered-common!
                     check-remembered-tagged!
                     check-remembered-node!
                     check-remembered-?!
                     has-fields
                     has-fields/common
                     has-fields/type
                     tagged-any-fields-type
                     tagged-any-fields-predicate
                     split/type
                     merge/type
                     tagged-struct-id?)
         tagged-get-field
         λ-tagged-get-field
         split
         merge
         with+
         with!
         with!!)

(provide (all-from-out (submod "." pre-declare)))

«check-remembered!»
«tagged-builder!»
«tagged-∀-builder!»
«tagged-infer-builder!»
«tagged-any-fields»
«tagged-type!»
«tagged-∀-type!»
«tagged-infer-type!»
«tagged-any-fields-type»
«tagged-predicate!»
«tagged-pred-predicate!»
«tagged-any-predicate!»
«tagged-any-fields-predicate»
«tagged-match!»
«tagged-anytag-match!»
«has-fields»
«has-fields/type»
«tagged-get-field»
«λ-tagged-get-field»
«split»
«merge»
«with+»
«with!»
«with!!»
«tagged-struct-id?»

B.3 Implementation of nodes: printing and equality

This section discusses the implementation of prop:custom-write and prop:equal+hash for nodes.

B.3.1 Printing nodes

B.3.2 Comparing and hashing nodes

B.3.2.1 Hashing nodes

B.3.2.2 Caching node equality

B.3.2.3 Comparing nodes for equality

Bibliography

B.3.1 Printing nodes

To avoid printing large and confusing swathes of data when a node is displayed, we only print its constituents up to a certain depth. The parameter write-node-depth controls the depth for printing nested nodes.

«write-node-depth» ::=

(define write-node-depth (make-parameter 1))

The make-node-writer macro expands to a procedure which prints a node with the given name and fields. If the write-node-depth is 0, then the contents of the node are elided, and only its name is printed, so that the resulting printed representation is "(node name …)" with an actual ellipsis character.

«node-custom-write» ::=

(define-syntax/parse (make-node-writer pid name fieldᵢ …)
  #'(λ (self out mode)
      (if (> (write-node-depth) 0)
          (parameterize ([write-node-depth (sub1 (write-node-depth))])
            (fprintf out
                     "(node ~a ~a)"
                     'name
                     (string-join (list «format-field» …) " ")))
          (fprintf out "(node ~a …)" 'name))))

Each field is formatted as [fieldᵢ valueᵢ]. Copy-pasting the whole printed form will not form a valid expression which would be equal? to the original. This limitation is deliberate: a node will often refer to many other nodes, and a stand-alone representation of such a node would result in a very large printed form. Instead, the user should call the serialize-graph macro, which will produce a complete, canonical The representation is canonical so long as unordered sets or hash tables are not used as part of the node's contents. In that case, the printed form is canonical modulo the order of elements within the set or hash table. Once executed, it will nevertheless produce a node which is equal? to the original. and self-contained representation of the node.

«format-field» ::=

(format "[~a ~a]" 'fieldᵢ (force ((struct-accessor pid fieldᵢ) self)))

B.3.2 Comparing and hashing nodes

Nodes are represented like tagged structures, but contain an extra raw field. The raw field contains a low-level representation of the node, which is used to implement node equality. The low-level representation uses the raw-node Racket struct. It contains two fields, database and index. The first is the database of nodes, as created by the graph construction macro. It contains one vector of nodes per node type. The second is a logical pointer into that database, consisting of the node’s type’s name, represented as a symbol, and an offset within the corresponding vector, represented as an Index.

«raw-node» ::=

(struct/props (D I) raw-node ([database : D] [index : I]) #:transparent
«raw-node-equality»)

A regular with-promises node can have several in-memory representations which are not pointer-equal. This is due to the fact that the contents of node fields are wrapped with promises, and accessing the node via two distinct paths will yield two copies, each with fresh promises. We therefore use the raw-node as a proxy for pointer equality: we know for sure that two nodes are exactly the same if the database and index is the same for both nodes.

«raw-node-equality» ::=

#:property prop:equal+hash
(list (λ (a b r)
        (and (raw-node? a)
             (raw-node? b)
             (eq? (raw-node-database a) (raw-node-database b))
             (equal? (raw-node-index a) (raw-node-index b))))
      (λ (a r)
        (bitwise-xor (eq-hash-code (raw-node-database a))
                     (r (raw-node-index a))))
      (λ (a r)
        (bitwise-xor (eq-hash-code (raw-node-database a))
                     (r (raw-node-index a)))))

The following function can then be used to test if two nodes are the same, based on the contents of their raw field:

«same-node?» ::=

(define (same-node? a b)
  (and ((struct-predicate node-id) a)
       ((struct-predicate node-id) b)
       (equal? ((struct-accessor node-id raw) a)
               ((struct-accessor node-id raw) b))))

To detect cycles within the graph while implementing node equality, we use a global hash table tracking which nodes have already been visited.

«seen-hash-table» ::=

(define seen-nodes
: (Parameterof (U #f (HashTable (raw-node Any Any) Any)))
(make-parameter #f))

The current implementation uses a mutable hash table. It is only initialised when equal? starts comparing two nodes, so that references to nodes are not kept once equal? finished running. However, in theory, an immutable hash table could be threaded through all the recursive calls to equal?. Unfortunately, the recursive equality function supplied by Racket when implementing prop:equal+hash does not accept an extra parameter to thread state throughout the recursion. It would therefore be necessary to re-implement the algorithm used by Racket’s equal? as described by [Efficient nondestructive equality checking for trees and graphs, Adams and Dybvig, 2008] tailored to the comparison of data structures with high-level logical cycles. To be correct, such a re-implementation would however need to access the prop:equal+hash property of other structs, but Racket provides no public predicate or accessor for that property. Therefore, although it would, in theory, be possible to implement node equality without mutable state, Racket’s library does not offer the primitives needed to build it. We therefore settle on using a global, mutable hash table, which will exist only during the execution of equal?.

«node-equal+hash» ::=

(define-syntax/parse
    (make-node-comparer common-id node-id name fieldᵢ …)
  (define-temp-ids "~a/τ" (fieldᵢ …))
  #'(let ()
      «same-node?»
      «find-in-table»
      «node-hash»
      (list «node-equal?»
            «node-equal-hash-code»
            «node-equal-secondary-hash-code»)))

B.3.2.1 Hashing nodes

equal-hash-code and equal-secondary-hash-code are implemented via a single function node-hash, the only difference being the function used to recursively compute the hash of sub-elements.

«node-equal-hash-code» ::=

(λ (a rec-equal-hash-code)
(node-hash a rec-equal-hash-code))

«node-equal-secondary-hash-code» ::=

(λ (a rec-equal-secondary-hash-code)
(node-hash a rec-equal-secondary-hash-code))

It would be desirable to implement hashing in the following way: if the current node is already present in a hash table of seen nodes, but is not eq? to that copy, then the racket hash function is called on the already-seen node. Otherwise, if the node has never been seen, or if it is eq? to the seen node, the hash code is computed.

The problem with this approach is that it introduces an intermediate recursive call to Racket’s hashing function. When Racket’s hashing function is applied to a structure with the prop:equal+hash property, it does not return the result of the struct’s hash implementation unmodified.

For example, the code below implements a struct s with no fields, which computes its hash code by recursively calling Racket’s hashing function on other (unique) instances of s, and returns the constant 1 at a certain depth. The custom hashing function does not alter in any way the result returned by Racket’s hashing function, however we can see that the hash for the same instance of s depends on the number of recursive calls to Racket’s hashing function r. This simple experiment seems to suggest that Racket adds 50 at each step, but this is not something that can be relied upon.

(define recursion-depth (make-parameter #f))
(struct s (x) #:transparent
  #:property prop:equal+hash
  (list (λ (a b r) (error "Not implemented"))
        (λ (a r)
          (if (= 0 (recursion-depth))
              1
              (parameterize ([recursion-depth (sub1 (recursion-depth))])
                (r (s (gensym))))))
        (λ (a r) (error "Not implemented"))))
(define s-instance (s 'x))

> (parameterize ([recursion-depth 0])
    (equal-hash-code s-instance))
47
> (parameterize ([recursion-depth 1])
    (equal-hash-code s-instance))
93
> (parameterize ([recursion-depth 2])
    (equal-hash-code s-instance))
139

Since the order of traversal of the nodes is not fixed in the presence of sets and hash tables, we need to make sure that the recursion depth at which a node’s hash is computed is constant. We achieve this by always calling Racket’s hash function on the already-seen node from the hash table, even if was inserted just now. To distinguish between the current node and the already-seen node from the hash table, we remove the contents of the node’s raw field, and replace them with a special marker.

«node-hash» ::=

(: node-hash (∀ (fieldᵢ/τ …)
                (→ (node-id fieldᵢ/τ … Any Any) (→ Any Integer) Integer)))
(define (node-hash nd racket-recur-hash)
  (if (eq? (raw-node-database ((struct-accessor node-id raw) nd))
           'unique-copy)
      «compute-hash»
      «hash-init-table-and-recur»))

When the node’s raw field does not indicate 'unique-copy, we first initialise the hash table if needed, then recursively call racket-recur-hash on the unique copy of the node:

«hash-init-table-and-recur» ::=

(let ([seen-table (or (seen-nodes)
                      ((inst make-hash (raw-node Any Any) Any)))])
  (parameterize ([seen-nodes seen-table])
    (racket-recur-hash (find-in-table seen-table nd))))

To obtain the unique copy of the node, we look it up in the hash table, creating it and adding it to the hash table if the current node is not already present there:

«find-in-table» ::=

(: find-in-table (∀ (fieldᵢ/τ …)
                    (→ (HashTable (raw-node Any Any) Any)
                       (node-id fieldᵢ/τ … Any Any)
                       Any)))
(define (find-in-table seen-table nd)
  (hash-ref! seen-table
             ((struct-accessor node-id raw) nd)
             (λ () «make-unique-copy-node»)))

To create a unique copy of the node, we create a new instance of the node’s struct, and copy over all the fields except for the raw field, whose value becomes 'unique-copy.

«make-unique-copy-node» ::=

((struct-constructor node-id) ((struct-accessor common-id fieldᵢ) nd)
…
(raw-node 'unique-copy 'unique-copy))

The hash code is finally computed by combining the hash code for each field’s contents (after forcing it). The node’s tag name is also hashed, and added to the mix.

«compute-hash» ::=

(combine-hash-codes
(racket-recur-hash 'name)
(racket-recur-hash (force ((struct-accessor common-id fieldᵢ) nd)))
…)

To combine hash codes, we simply compute their xor. Later versions of this library may use more sophisticated mechanisms.

«combine-hash-codes» ::=

(: combine-hash-codes (→ Integer * Integer))
(define (combine-hash-codes . hashes)
(apply bitwise-xor hashes))

B.3.2.2 Caching node equality

We provide a mechanism at run-time to cache the result of equality tests within a limited dynamic scope. The graph generation procedure can coalesce nodes which are equal?, which means that it needs to perform a significant number of equality comparisons, and can therefore benefit from caching the result of inner equality tests during the execution of the coalescing operation.

«equality-cache» ::=

(define equality-cache
  : (Parameterof (U #f (HashTable (Pairof (raw-node Any Any)
                                          (raw-node Any Any))
                                  Boolean)))
  (make-parameter #f))

The with-node-equality-cache form executes its body while enabling caching of the result of direct and recursive calls to equal? on nodes.

«with-node-equality-cache» ::=

(define-syntax-rule (with-node-equality-cache . body)
  (parameterize ([equality-cache (or (equality-cache)
                                     «make-equality-cache»)])
    . body))

If necessary, a new equality cache is created, unless with-node-equality-cache is used within the dynamic extent of another use of itself.

«make-equality-cache» ::=

((inst make-hash (Pairof (raw-node Any Any) (raw-node Any Any)) Any))

When comparing two nodes, we first check whether an equality cache is installed. If so, we attempt to query the cache, and memoize the result of the comparison when the pair of values is not already in the cache.

«memoize-equality» ::=

(λ (result-thunk)
  (let ([e-cache (equality-cache)])
    (if e-cache
        (cond
          [(hash-has-key? e-cache (cons a-raw b-raw))
           (hash-ref e-cache (cons a-raw b-raw))]
          [(hash-has-key? e-cache (cons b-raw a-raw))
           (hash-ref e-cache (cons b-raw a-raw))]
          [else
           (let ([result (result-thunk)])
             (hash-set! e-cache (cons a-raw b-raw) result)
             result)])
        (result-thunk))))

B.3.2.3 Comparing nodes for equality

We implement equality following the same architecture as for hash codes, but check that both nodes are already unique copies. In addition, the implementation of equal? checks that both values are of the node’s type.

«node-equal?» ::=

(λ (a b racket-recur-equal?)
  (and ((struct-predicate node-id) a)
       ((struct-predicate node-id) b)
       (let ([a-raw ((struct-accessor node-id raw) a)]
             [b-raw ((struct-accessor node-id raw) b)])
         (if (and (eq? (raw-node-database a-raw) 'unique-copy)
                  (eq? (raw-node-database b-raw) 'unique-copy))
             «compare»
             (or (same-node? a b)
                 («memoize-equality»
                  (λ () «equality-init-table-and-recur»)))))))

When either or both of the node’s raw field do not indicate 'unique-copy, we first initialise the hash table if needed, then recursively call racket-recur-hash on the unique copy of each node:

«equality-init-table-and-recur» ::=

(let ([seen-table (or (seen-nodes)
                      ((inst make-hash (raw-node Any Any) Any)))])
  (parameterize ([seen-nodes seen-table])
    (racket-recur-equal? (find-in-table seen-table a)
                         (find-in-table seen-table b))))

The nodes are compared pointwise, checking each pair of fields for equality, after forcing both:

«compare» ::=

(and (racket-recur-equal? (force ((struct-accessor common-id fieldᵢ) a))
(force ((struct-accessor common-id fieldᵢ) b)))
…)

«*» ::=

(require racket/promise
         racket/string
         racket/require
         phc-toolkit
         remember
         typed-struct-props
         (for-syntax racket/base
                     racket/syntax
                     racket/list
                     racket/set
                     racket/format
                     (subtract-in syntax/stx phc-toolkit/untyped)
                     syntax/parse
                     phc-toolkit/untyped))

(provide make-node-comparer
         make-node-writer
         raw-node
         write-node-depth
         with-node-equality-cache)

«equality-cache»
«with-node-equality-cache»
«seen-hash-table»
«write-node-depth»
«node-custom-write»
«raw-node»
«combine-hash-codes»
«node-equal+hash»

Bibliography

[Efficient nondestructive equality checking for trees and graphs, Adams and Dybvig, 2008]

Michael D. Adams and R. Kent Dybvig, “Efficient nondestructive equality checking for trees and graphs in ACM Sigplan Notices (Vol. 43, No. 9) pp. 179–188.” 2008. http://www.cs.indiana.edu/~dyb/pubs/equal.pdf

B.4 Implementation of ADTs: syntax scopes

Due to TR bug #399, structs declared by a macro do not work if the macro itself is declared in a separate module. This seems to be due to the extra scope added as pieces of syntax cross the module boundary. There is unfortunately no equivalent to syntax-local-introduce that could be used to flip this module scope.

We therefore require the user to call (set-adt-context) at the beginning of the file. This macro stores the scopes present where it was called in a mutable for-syntax variable:

«adt-context»1 ::=

(define-for-syntax mutable-adt-context (box #f))

These scopes are later used as the context for struct identifiers:

«ctx-introduce» ::=

(define-for-syntax (ctx-introduce id)
  (unless (unbox mutable-adt-context)
    (raise-syntax-error 'adt
                        (~a "(adt-init) must be called in the"
                            " file (or REPL). ") id))
  (struct-identifier-fresh-introducer
   (replace-context (syntax-local-introduce
                     (unbox mutable-adt-context))
                    id)))

The (set-adt-context) macro should be called at the beginning of the file or typed in the REPL before using structures. It simply stores the syntax used to call it in mutable-adt-context.

«adt-context»2 ::=

(define-for-syntax (set-adt-context ctx)
  (set-box! mutable-adt-context ctx))

(define-syntax (set-adt-context-macro stx)
  (syntax-case stx ()
    [(_ ctx)
     (begin (set-box! mutable-adt-context #'ctx)
            #'(void))]))

For debugging purposes, we provide a macro and a for-syntax function which show the current ADT context (i.e. the list of scopes).

«adt-context»3 ::=

(define-for-syntax (debug-show-adt-context)
  (displayln
   (hash-ref (syntax-debug-info (unbox mutable-adt-context))
             'context)))
(define-syntax (debug-show-adt-context-macro stx)
  (debug-show-adt-context)
  #'(define dummy (void)))

The struct identifiers are introduced in a fresh scope Due to TR bug #399, this feature is temporarily disabled, until the bug is fixed., so that they do not conflict with any other user value.

«fresh-introducer» ::=

(define-for-syntax struct-identifier-fresh-introducer
(λ (x) x))

We provide two ways of checking whether set-adt-context was called: (adt-context?) returns a boolean, while (check-adt-context) raises an error when set-adt-context has not been called.

«adt-context?» ::=

(define-for-syntax (adt-context?)
(true? (unbox mutable-adt-context)))

«check-adt-context» ::=

(define-for-syntax (check-adt-context)
  (unless (adt-context?)
    (raise-syntax-error 'phc-adt
                        (string-append
                         "adt-init must be called before"
                         " using the features in phc-adt"))))

B.4.1 Putting it all together

«*» ::=

(begin
  (require (for-syntax racket/base
                       racket/syntax
                       racket/set
                       racket/list
                       racket/format
                       phc-toolkit/untyped
                       syntax/strip-context)
           racket/require-syntax
           type-expander
           phc-toolkit
           remember))

(provide (for-syntax set-adt-context)
         set-adt-context-macro
         debug-show-adt-context-macro)

(begin-for-syntax
  (provide debug-show-adt-context
           adt-context?
           check-adt-context
           ctx-introduce))

«adt-context»
«fresh-introducer»
«ctx-introduce»
«adt-context?»
«check-adt-context»

B.5 User API for tagged structures

B.5.1 Overview of the implementation of structures

B.5.2 A polyvalent identifier: type, match, constructor and instance

B.5.3 The tagged call expander (builder and instance)

B.5.3.1 Call to tagged with no fields: instance or constructor?

B.5.3.2 Signature for the tagged call expander

B.5.3.3 Implementation

B.5.4 Type expander

B.5.4.1 The TaggedTop type

B.5.5 Match expander

B.5.6 Predicates for tagged structures

B.5.6.1 The TaggedTop? predicate

B.5.7 Defining shorthands with define-tagged

B.5.8 Implementation of uniform-get

B.5.9 Putting it all together

B.5.1 Overview of the implementation of structures

Tagged structures are represented using regular Racket structs, see Somewhat outdated overview of the implementation choices for structures, graphs and passes for a somewhat outdated discussion of alternative possibilities.

The ADT type system implemented by this library needs to know about all declared structures across the program, so that fields can be accessed anonymously, e.g. (get instance f) instead of the traditional (s-f instance) (where s is the struct’s identifier, and f is the field name). This allows the accessor get to work on all structures which contain a field with the given name (and therefore plays well with unions of structures which share some fields). It also avoids the need to specify the struct which declared a field in order to accessing it. A separate library adds a coat of syntactic sugar to enable the notation instance.f1.f2.f3, following the well-known convention often used by object-oriented languages.

The section Low-level implementation of tagged structures describes the low-level implementation of tagged structures, including how all declared structures are remembered across compilations, and the implementation of the basic operations on them: constructor, predicate, accessor, type, match expander, and row polymorphism (also known as static duck typing). The implementation of row polymorphism works by querying the list of all known tagged structures and returns those containing a given set of fields.

B.5.2 A polyvalent identifier: type, match, constructor and instance

The tagged identifier can be used to describe a tagged structure type, a match pattern, a tagged structure builder function, or to directly create an instance. The last two cases are handled by the <call-expander>.

«tagged» ::=

(define-multi-id tagged
  #:type-expander  tagged-type-expander
  #:match-expander tagged-match-expander
  #:call           tagged-call-expander)

B.5.3 The tagged call expander (builder and instance)

When called like a macro, tagged accepts several syntaxes:

(tagged name [fieldᵢ] …+) or (tagged name fieldᵢ …+), which return a builder function which has a type argument τᵢ corresponding to each fieldᵢ’s type.
«call [fieldᵢ] …+» ::=
(~seq {~either [fieldᵢ:id] fieldᵢ:id} …+
      {~global-or builder?}
      {~global-or no-types?}
      {~post-fail «no-values-error» #:when (attribute instance?)})
This clause implies the creation of a builder function, so if #:instance is specified, the following error is raised:
«no-values-error» ::=
(~a "The #:instance keyword implies the use of [field value],"
    " [field : type value] or [field value : type].")
(tagged name [fieldᵢ valueᵢ] …+), which returns an instance, inferring the type of the fields
«call [fieldᵢ : τᵢ] …+» ::=
(~seq [fieldᵢ:id C:colon τᵢ:expr] …+
      {~global-or builder?}
      {~global-or types?}
      {~post-fail «no-values-error» #:when (attribute instance?)})
This clause implies the creation of an instance, so if #:builder is specified, the following error is raised:
«values-error» ::=
(~a "The #:builder keyword implies the use of [field], field"
    " or [field : type].")
(tagged name [fieldᵢ : τᵢ] …+), which returns a constructor with the given types
«call [fieldᵢ valueᵢ] …+» ::=
(~seq [fieldᵢ:id valueᵢ:expr] …+
      {~global-or instance?}
      {~global-or no-types?}
      {~post-fail «values-error» #:when (attribute builder?)})
This clause implies the creation of a builder function, so if #:instance is specified, the following error is raised:
(no-values-error) ::=
(~a "The #:instance keyword implies the use of [field value],"
    " [field : type value] or [field value : type].")

(tagged name [fieldᵢ valueᵢ : τᵢ] …+), which returns an instance using the given types

«call [fieldᵢ valueᵢ : τᵢ] …+» ::=

(~seq (~either [fieldᵢ:id valueᵢ:expr C:colon τᵢ:expr]
               [fieldᵢ:id C:colon τᵢ:expr valueᵢ:expr])
      …+
      {~global-or instance?}
      {~global-or types?}
      {~post-fail «values-error» #:when (attribute builder?)})

This clause implies the creation of an instance, so if #:builder is specified, the following error is raised:

(values-error) ::=

(~a "The #:builder keyword implies the use of [field], field"
" or [field : type].")

B.5.3.1 Call to tagged with no fields: instance or constructor?

A call to (tagged) with no field is ambiguous: it could return a constructor function for the structure with no fields, or an instance of that structure.

(tagged)

We tried to make a hybrid object using define-struct/exec which would be an instance of the structure with no fields, but could also be called as a function (which would return itself). Unfortunately, this use case is not yet fully supported by Typed/Racket: the instance cannot be annotated as a function type, or passed as an argument to a higher-order function (Typed/Racket issue #430). This can be circumvented by using unsafe operations to give the instance its proper type (Rec R (∩ (→ R) struct-type)), but Typed/Racket does not consider this type applicable, and an annotation is required each time the instance is used as a builder function (Typed/Racket issue #431.

We therefore added two optional keywords, #:instance and #:builder, which can be used to disambiguate. They can also be used when fields respectively with or without values are specified, so that macros don’t need to handle the empty structure as a special case.

B.5.3.2 Signature for the tagged call expander

When called as a macro, tagged expects:

The tagged structure’s tag name:
«name-id-mixin» ::=
(define-eh-alternative-mixin name-id-mixin
(pattern
(~once (~order-point name-order-point name:id))))
An optional list of type variables, preceded by #:∀:
«∀-mixin» ::=
(define-eh-alternative-mixin ∀-mixin
(pattern {~optional (~seq #:∀ ({~named-seq tvarᵢ :id …})
(~global-or tvars?))}))

Either of the #:builder or #:instance options, or none:

«tagged-call-instance-or-builder-mixin» ::=

(define-eh-alternative-mixin tagged-call-instance-or-builder-mixin
  (pattern
   (~optional (~and instance-or-builder
                    (~or {~global-or instance? #:instance}
                         {~global-or builder? #:builder}))
              #:name "either #:instance or #:builder")))

An optional list of fields, possibly annotated with a type, and possibly associated to a value:

«tagged-call-fields-mixin» ::=

(define-eh-alternative-mixin tagged-call-fields-mixin
  (pattern
   (~optional/else
    (~try-after name-order-point «name-after-field-error»
                (~or «call [fieldᵢ] …+»
                     «call [fieldᵢ : τᵢ] …+»
                     «call [fieldᵢ valueᵢ] …+»
                     «call [fieldᵢ valueᵢ : τᵢ] …+»))
    #:defaults ([(fieldᵢ 1) (list)]
                [(valueᵢ 1) (list)]
                [(τᵢ 1) (list)])
    #:else-post-fail «empty-err» #:unless (or (attribute builder?)
                                              (attribute instance?))
    #:name (~a "field or [field] or [field : type] for #:builder,"
               " [field value] or [field : type value]"
               " or [field value : type] for #:instance"))))

When no fields are specified, the following error is raised unless either #:builder or #:instance is specified.

«empty-err» ::=

(~a "If no fields are specified, then either #:builder or #:instance"
" must be present")

The four elements can appear in any order, with one constraint: the name must appear before the first field descriptor. Not only does it make more sense semantically, but it also avoids ambiguities when the list of field names is just a list of plain identifiers (without any type or value).

«name-after-field-error» ::=

"the name must appear before any field"

We can now combine all four mixins.

«tagged-call-args-mixin» ::=

(define-eh-alternative-mixin tagged-call-args-mixin
  #:define-splicing-syntax-class tagged-call-args-syntax-class
  (pattern {~mixin name-id-mixin})
  (pattern {~mixin tagged-call-instance-or-builder-mixin})
  (pattern {~mixin tagged-call-fields-mixin})
  (pattern {~mixin ∀-mixin}))

B.5.3.3 Implementation

The call expander uses the low-level functions tagged-builder!, tagged-∀-builder! and tagged-infer-builder! implemented in Creating instances of a tagged structure. The first returns the syntax for a builder function for the given tagged structure. The second returns the syntax for a polymorphic builder function for the given tagged structure, using the given type variables which are bound inside the field type declarations. The last returns the syntax for a polymorphic builder function for the given tagged structure, with one type parameter per field, which allows the type of each field to be inferred.

«call-expander» ::=

(define/syntax-parse+simple
(tagged-call-expander :tagged-call-args-syntax-class)
«call-expander-cases»)

If type variables are present, then tagged-∀-builder! is used. Otherwise, if types are specified, then tagged-builder! is used, otherwise tagged-infer-builder! is used.

«call-expander-cases»1 ::=

(define/with-syntax f
  (if (attribute tvars?)
      (tagged-∀-builder! #'((tvarᵢ …) name [fieldᵢ : τᵢ] …))
      (if (attribute types?)
          (tagged-builder! #'(name [fieldᵢ τᵢ] …))
          (tagged-infer-builder! #'(name fieldᵢ …)))))

If the #:instance keyword was specified, or if values are specified for each field, the builder function is immediately called with those values, in order to produce an instance of the tagged structure. Otherwise, the builder function itself is produced.

«call-expander-cases»2 ::=

(if (attribute instance?)
#'(f valueᵢ …)
#'f)

B.5.4 Type expander

When used as a type expander, tagged expects:

The tagged structure’s tag name, as defined for the call expander in «name-id-mixin»
An optional list of type variables, as defined for the call expander in «∀-mixin»

An optional list of fields, possibly annotated with a type:

«tagged-type-fields-mixin» ::=

(define-eh-alternative-mixin tagged-type-fields-mixin
  (pattern
   (~optional
    (~try-after name-order-point «name-after-field-error»
                (~named-seq field-declarations
                  (~or «[fieldᵢ] …+»
                       «[fieldᵢ τᵢ] …+»)))
    #:defaults ([(fieldᵢ 1) (list)]
                [(τᵢ 1) (list)])
    #:name "field or [field] or [field type] or [field : type]")))

The main difference with the allowed field specifications for the call expander are that values are not allowed. Furthermore, the : between a field and its type is optional:

«[fieldᵢ τᵢ] …+» ::=

(~seq [fieldᵢ:id {~optional C:colon} τᵢ:expr] …+
{~global-or types?})

Furthermore, the instance? and builder? attributes are not meaningful for the type expander.

«[fieldᵢ] …+» ::=

(~seq {~either [fieldᵢ:id] fieldᵢ:id} …+
{~global-or no-types?})

The three elements can appear in any order, with the same constraint as for the call expander: the name must appear before the first field descriptor.

(name-after-field-error) ::=

"the name must appear before any field"

«tagged-type-args-mixin» ::=

(define-eh-alternative-mixin tagged-type-args-mixin
  #:define-splicing-syntax-class tagged-type-args-syntax-class
  (pattern {~mixin name-id-mixin})
  (pattern {~mixin tagged-type-fields-mixin})
  (pattern {~mixin ∀-mixin}))

The type expander uses the low-level functions tagged-type!, tagged-∀-type! and tagged-infer-type! implemented in Type of a tagged structure. The first returns the syntax for the type for the given tagged structure. The second returns the syntax for a polymorphic type for the given tagged structure, using the given type variables which are bound inside the field type declarations. The last returns the syntax for a polymorphic type for the given tagged structure, with one type parameter per field, which allows the type of each field to be inferred or filled in later.

«type-expander» ::=

(define/syntax-parse+simple
(tagged-type-expander :tagged-type-args-syntax-class)
«type-expander-cases»)

If type variables are present, then tagged-∀-type! is used. Otherwise, if types are specified, then tagged-type! is used, otherwise tagged-infer-type! is used.

«type-expander-cases» ::=

(if (attribute tvars?)
    (tagged-∀-type! #'((tvarᵢ …) name [fieldᵢ : τᵢ] …))
    (if (attribute types?)
        (tagged-type! #'(name [fieldᵢ τᵢ] …))
        (tagged-infer-type! #'(name fieldᵢ …))))

B.5.4.1 The TaggedTop type

The TaggedTop type is extracted from the low-level TaggedTop-struct identifier (which is a struct identifier). The TaggedTop type includes not only tagged structures, but also nodes.

«TaggedTop»1 ::=

(define-type TaggedTop TaggedTop-struct)

Additionally, the TaggedTop? predicate is simply aliased from the low-level TaggedTop-struct?.

«TaggedTop»2 ::=

(define TaggedTop? TaggedTop-struct?)

B.5.5 Match expander

When used as a match expander, tagged expects:

The tagged structure’s tag name, as defined for the call expander in «name-id-mixin»
The #:no-implicit-bind, which specified that the field name should not automatically be bound by the match pattern to the field’s contents:
«tagged-match-no-implicit-bind-mixin» ::=
(define-eh-alternative-mixin tagged-match-no-implicit-bind-mixin
(pattern (~optional (~global-or no-implicit #:no-implicit-bind))))

A (possibly empty) list of fields, each associated with zero or more patterns:

«tagged-match-fields-mixin» ::=

(define-eh-alternative-mixin tagged-match-fields-mixin
  (pattern
   (~maybe/empty
    (~try-after name-order-point «name-after-field-error»
                «[fieldᵢ patᵢⱼ …] …+»)
    #:name (~a "field or [field pat …]"))))

The main differences with the allowed field specifications for the call expander are that values and types are not allowed, but instead the field name may be followed by match patterns:

«[fieldᵢ patᵢⱼ …] …+» ::=

(~seq (~either {~and fieldᵢ:id {~bind [(patᵢⱼ 1) (list)]}}
[fieldᵢ:id patᵢⱼ:expr …])
…+)

The three elements can appear in any order, with the same constraint as for the call expander: the name must appear before the first field descriptor.

(name-after-field-error) ::=

"the name must appear before any field"

«tagged-match-args-mixin» ::=

(define-eh-alternative-mixin tagged-match-args-mixin
  #:define-syntax-class tagged-match-args-syntax-class
  (pattern {~mixin name-id-mixin})
  (pattern {~mixin tagged-match-no-implicit-bind-mixin})
  (pattern {~mixin tagged-match-fields-mixin}))

The match expander uses the low-level function tagged-match! implemented in Type of a tagged structure. It returns the syntax for a match pattern for the given tagged structure. The resulting match pattern checks that the value is an instance of a tagged structure with the given name and fields, and matches the value of each field against the corresponding pattern.

«match-expander» ::=

(define/syntax-parse+simple
(tagged-match-expander . :tagged-match-args-syntax-class)
«match-expander-body»)

Unless #:no-implicit-bind is specified, we include the field name as part of the pattern, so that field names are bound to the field’s contents.

«match-expander-body» ::=

(if (attribute no-implicit)
(tagged-match! #'(name [fieldᵢ (and patᵢⱼ …)] …))
(tagged-match! #'(name [fieldᵢ (and fieldᵢ patᵢⱼ …)] …)))

B.5.6 Predicates for tagged structures

«tagged?» ::=

(define-syntax tagged?
  (syntax-parser
    [(_ name fieldᵢ:id …)
     (tagged-any-predicate! #'(name fieldᵢ …))]
    [(_ name [fieldᵢ:id :colon τᵢ:type] …)
     (tagged-predicate! #'(name [fieldᵢ τᵢ] …))]
    [(_ name [fieldᵢ:id predᵢ:type] …)
     (tagged-pred-predicate! #'(name [fieldᵢ predᵢ] …))]))

B.5.6.1 The TaggedTop? predicate

The TaggedTop? predicate is simply re-provided. It is initially defined in Common ancestor to all tagged structures: TaggedTop-struct.

«provide TaggedTop?» ::=

(provide (rename-out [TaggedTop-struct? TaggedTop?]))

B.5.7 Defining shorthands with define-tagged

The define-tagged macro can be used to bind to an identifier the type expander, match expander, predicate and constructor function for a given tagged structure.

The define-tagged macro expects:

The tagged structure’s tag name, as defined for the call expander in «name-id-mixin»
An optional list of type variables, as defined for the call expander in «∀-mixin»
A possibly empty list of fields, possibly annotated with a type, as defined for the type expander in «tagged-type-fields-mixin»
Optionally, the tag name to be used, specified with #:tag tag-name:
«tag-kw-mixin» ::=
(define-eh-alternative-mixin tag-kw-mixin
(pattern {~optional {~seq #:tag explicit-tag «default-tag-name»}}))
The tag name defaults to name, i.e. the identifier currently being defined.
«default-tag-name» ::=
{~post-check
{~bind [tag-name (or (attribute explicit-tag)
#'name)]}}
Optionally, a name for the predicate, specified with #:? predicate-name?:
«predicate?-mixin» ::=
(define-eh-alternative-mixin predicate?-mixin
(pattern {~optional {~seq #:? predicate? «default-name?»}}))
The predicate name defaults to name?, where name is the identifier currently being defined.
«default-name?» ::=
{~post-check
{~bind [name? (or (attribute predicate?)
(format-id/record #'name "~a?" #'name))]}}

The five elements can appear in any order, with the same constraint as for the call expander: the name must appear before the first field descriptor.

«define-tagged-args-mixin» ::=

(define-eh-alternative-mixin define-tagged-args-mixin
  #:define-splicing-syntax-class define-tagged-args-syntax-class
  (pattern (~or {~mixin name-id-mixin}
                {~mixin tag-kw-mixin}
                {~mixin tagged-type-fields-mixin}
                {~mixin predicate?-mixin}
                {~mixin ∀-mixin})))

The define-tagged macro is then implemented using define-multi-id:

«define-tagged» ::=

(define-syntax/parse+simple
    (define-tagged :define-tagged-args-syntax-class)
  (define-temp-ids "~a/pat" (fieldᵢ …))
  (quasisyntax/top-loc stx
    (begin
      (define-multi-id name
        #:type-expander    (make-id+call-transformer
                            #'«type-expander/define»)
        #:match-expander   «match-expander/define»
        #:else             «else-expander/define»)
      (define name?        «predicate/define»))))

The type expander handles the same three cases as for tagged: with type variables, with a type for each field, or inferred.

«type-expander/define» ::=

#,(if (attribute tvars?)
      (tagged-∀-type! #'((tvarᵢ …) tag-name [fieldᵢ τᵢ] …))
      (if (attribute types?)
          (tagged-type! #'(tag-name [fieldᵢ τᵢ] …))
          (tagged-infer-type! #'(tag-name fieldᵢ …))))

The match expander is a short form of the one implemented for tagged, as it takes only one positional pattern per field.

«match-expander/define» ::=

(λ (stx2)
  (syntax-case stx2 ()
    [(_ fieldᵢ/pat …)
     (tagged-match! #'(tag-name [fieldᵢ fieldᵢ/pat] …))]
    ;Todo: implement a "rest" pattern))

Otherwise, when name is called as a function, or used as an identifier on its own, we produce a builder function. When name is called as a function, the builder function is applied immediately to the arguments, otherwise the builder function itself is used. The same three cases as for tagged are handled: with type variables, with a type for each field, or inferred.

«else-expander/define» ::=

#'#,(if (attribute tvars?)
        (tagged-∀-builder!
         #'((tvarᵢ …) tag-name [fieldᵢ τᵢ] …))
        (if (attribute types?)
            (tagged-builder! #'(tag-name [fieldᵢ τᵢ] …))
            (tagged-infer-builder! #'(tag-name fieldᵢ …))))

Finally, we define the predicate name?. Contrarily to tagged?, it does not take into account the field types, as we have no guarantee that Typed/Racket’s make-predicate works for those. Instead, name? recognises any instance of a tagged structure with the given tag name and fields. If a more accurate predicate is desired, it can easily be implemented using tagged?.

«predicate/define» ::=

#,(tagged-any-predicate! #'(tag-name fieldᵢ …))

B.5.8 Implementation of uniform-get

uniform-get operates on tagged structures. It retrieves the desired field from the structure, and forces it to obtain the actual value.

It is implemented as tagged-get-field in Accessing fields of tagged structures, and is simply re-provided here.

B.5.9 Putting it all together

«*» ::=

(require (for-syntax racket/base
                     racket/syntax
                     syntax/parse
                     phc-toolkit/untyped
                     syntax/strip-context
                     racket/function
                     extensible-parser-specifications
                     racket/format
                     type-expander/expander)
         phc-toolkit
         multi-id
         type-expander
         racket/promise
         "tagged-structure-low-level.hl.rkt"
         racket/format)

(define-syntax uniform-get
  (make-rename-transformer #'tagged-get-field))
(define-syntax λuniform-get
  (make-rename-transformer #'λ-tagged-get-field))
(provide uniform-get
         λuniform-get
         tagged
         tagged?
         define-tagged
         TaggedTop
         TaggedTop?

         (for-syntax tagged-call-args-syntax-class
                     tagged-call-expander-forward-attributes
                     tagged-call-expander

                     tagged-type-args-syntax-class
                     tagged-type-expander-forward-attributes
                     tagged-type-expander

                     tagged-match-args-syntax-class
                     tagged-match-expander-forward-attributes
                     tagged-match-expander

                     define-tagged-args-syntax-class
                     define-tagged-forward-attributes))

(begin-for-syntax
  «∀-mixin»
  «name-id-mixin»
  «tagged-call-instance-or-builder-mixin»
  «tagged-call-fields-mixin»
  «tagged-call-args-mixin»
  «tagged-type-fields-mixin»
  «tagged-type-args-mixin»
  «tagged-match-fields-mixin»
  «tagged-match-no-implicit-bind-mixin»
  «tagged-match-args-mixin»

  «predicate?-mixin»
  «tag-kw-mixin»
  «define-tagged-args-mixin»)

(begin-for-syntax
  «call-expander»
  «type-expander»
  «match-expander»)
«tagged»
«tagged?»
«TaggedTop»
«define-tagged»

B.6 Supertypes of tagged structures

B.6.1 type-expander

«tagged-supertype» ::=

(define-multi-id tagged-supertype
#:type-expander «tagged-supertype-type-expander»
#:match-expander «tagged-supertype-match-expander»)

As a type, tagged-supertype accepts two syntaxes. With the first one, the type of each field is specified, and the second returns a parametric structure:

«tagged-supertype-type-expander-signature-types» ::=

(_ name:id [field:id (~optional :colon) type:expr] …)

«tagged-supertype-type-expander-signature-infer» ::=

(_ name (~either [field:id] field:id) …)

The type uses the structure type-expander, and expands to the union of all structures which contain a superset of the given set of fields. It uses the specified type for the given fields, and defaults to Any for the other extra fields.

«tagged-supertype-type-expander-impl-types» ::=

(has-fields/type #'([field type] …))

The second syntax builds upon the first, and produces a parametric type, with a ∀ type argument for each specified field (other fields still falling back to Any).

«tagged-supertype-type-expander-impl-infer» ::=

(define-temp-ids "~a/τ" (field …))
#`(∀ (field/τ …)
#,(has-fields/type #'([field field/τ] …)))

The type-expander finally calls either case depending on the syntax used.

«tagged-supertype-type-expander» ::=

(λ (stx)
  (syntax-parse stx
    [«tagged-supertype-type-expander-signature-types»
     «tagged-supertype-type-expander-impl-types»]
    [«tagged-supertype-type-expander-signature-infer»
     «tagged-supertype-type-expander-impl-infer»]))

B.6.2 Match

The match-expander for tagged-supertype accepts all structures which contain a superset of the given set of fields:

«tagged-supertype-match-expander» ::=

(λ/syntax-parse (_ . :tagged-match-args-syntax-class)
  (define/with-syntax ([common . (all-field …)] …)
    (has-fields/common #'(fieldᵢ …)))
  (define/with-syntax ((maybe-fieldᵢ …) …)
    (if (attribute no-implicit)
        (map (const #'()) #'(fieldᵢ …))
        #'((fieldᵢ) …)))
  (define/with-syntax ((maybe-pats …) …)
    (quasitemplate ((«maybe-pat…» …) …)))
  #`(or (tagged name #:no-implicit-bind [all-field . maybe-pats] …) …))

«tagged-anytag-match» ::=

(define-match-expander tagged-anytag-match
(λ/syntax-case ([fieldᵢ patᵢⱼ …] …) ()
(tagged-anytag-match! #'([fieldᵢ (and patᵢⱼ …)] …))))

Each field that was passed to tagged-supertype additionally matches against the given pat …, and other fields do not use any extra pattern.

«maybe-pat…» ::=

(!cdr-assoc #:default []
            all-field
            [fieldᵢ . [maybe-fieldᵢ … patᵢⱼ …]]
            …)

B.6.3 Nested supertype

The (tagged-supertype* f₁ f₂ … fₙ T) type describes any structure containing a field f₁, whose type is any structure containing a field f₂ etc. The last field’s type is given by T.

«tagged-supertype*» ::=

(define-multi-id tagged-supertype*
  #:type-expander
  (λ (stx)
    (error (string-append "tagged-supertype* is currently broken (needs"
                          " to ignore the tag name, since it doe not"
                          " have a tag at each step."))
    (syntax-parse stx
      [(_ T:expr)
       #`T]
      [(_ T:expr field:id other-fields:id …)
       #`(tagged-supertype
          [field (tagged-supertype* T other-fields …)])]))
  ;#:match-expander <tagged-supertype-match-expander> ; TODO)

B.6.4 Conclusion

«*» ::=

(require (for-syntax racket/base
                     racket/function
                     racket/syntax
                     syntax/parse
                     syntax/parse/experimental/template
                     phc-toolkit/untyped
                     type-expander/expander)
         phc-toolkit
         multi-id
         type-expander
         "tagged-structure-low-level.hl.rkt"
         "tagged.hl.rkt")

(provide tagged-supertype
         tagged-supertype*)

«tagged-anytag-match»
«tagged-supertype»
«tagged-supertype*»

B.7 User API for untagged structures

B.7.1 Introduction

B.7.2 Defining untagged structures with define-structure

B.7.3 Implementation of StructureTop and StructureTop?

B.7.4 Supertypes for structures

B.7.5 Putting it all together

B.7.1 Introduction

Untagged structures are implemented exactly like tagged structures, except that they always use the untagged tag name.

«structure» ::=

(define-multi-id structure
  #:type-expander  «expand-to-tagged»
  #:match-expander «expand-to-tagged»
  #:call           «expand-to-tagged»)

All three cases simply expand to (tagged. (untagged . original-arguments)).

«expand-to-tagged» ::=

(λ/syntax-case (_ . original-arguments) ()
(syntax/top-loc stx
(tagged untagged . original-arguments)))

The structure? predicate is implemented in the same way:

«structure?» ::=

(define-syntax structure?
  (λ/syntax-case (_ . original-arguments) ()
    (syntax/top-loc stx
      (tagged? untagged . original-arguments))))

B.7.2 Defining untagged structures with define-structure

The define-structure expands to the (define-tagged. (#:tag. (untagged . original-arguments))), which uses define-tagged but forces the tag name to be untagged.

«define-structure» ::=

(define-syntax/case (define-structure . original-arguments) ()
(syntax/top-loc stx
(define-tagged #:tag untagged . original-arguments)))

B.7.3 Implementation of StructureTop and StructureTop?

The StructureTop? predicate is defined in terms of tagged-any-fields-predicate:

«StructureTop?» ::=

(define-syntax StructureTop?
(make-id+call-transformer-delayed
(λ () (tagged-any-fields-predicate #'untagged))))

Similarly, the StructureTop type is defined using tagged-any-fields-type:

«StructureTop» ::=

(define-type-expander (StructureTop stx)
  (syntax-case stx ()
    [id
     (identifier? #'id)
     (tagged-any-fields-type #'untagged)]))

B.7.4 Supertypes for structures

Like the structure and structure? identifiers, structure-supertype is defined in terms of its tagged structure counterpart, tagged-supertype:

«structure-supertype» ::=

(define-multi-id structure-supertype
#:type-expander «expand-to-tagged-supertype»
#:match-expander «expand-to-tagged-supertype»)

«expand-to-tagged-supertype» ::=

(λ/syntax-case (_ . original-arguments) ()
(syntax/top-loc stx
(tagged-supertype untagged . original-arguments)))

B.7.5 Putting it all together

«*» ::=

(require phc-toolkit
         "tagged.hl.rkt"
         "tagged-structure-low-level.hl.rkt"
         "tagged-supertype.hl.rkt"
         multi-id
         type-expander
         (for-syntax racket/base
                     phc-toolkit/untyped))

(provide structure
         structure?
         define-structure
         StructureTop
         StructureTop?
         structure-supertype)

«structure»
«structure?»
«define-structure»
«StructureTop»
«StructureTop?»
«structure-supertype»

B.8 User API for constructors

B.8.1 Introduction

B.8.2 The polyvalent identifier constructor: type, match, builder and instance

B.8.3 Type-expander

B.8.4 Match-expander

B.8.5 Predicate

B.8.6 Instance creation

B.8.7 Defining shorthands for constructors with define-constructor

B.8.8 Miscellanea

B.8.9 Putting it all together

B.8.1 Introduction

This file defines constructor, a form which allows tagging values, so that two otherwise identical values can be distinguished by the constructors used to wrap them. Coupled with the variants defined by this library, it implements a slight variation on the constructors and variants commonly found in other languages. The constructor form is effectively a wrapper around tagged structures, which stores all values within a single field named values.

The constructors defined in this library are "interned", meaning that two constructors in different files will be the same if they use same tag name. In other words, the tag of a constructor works in the same way as a symbol in Racket: unless otherwise specified, the same string of characters will always produce the same symbol, even across modules. The same goes for constructors: the same constructor name will always refer to the same type.

B.8.2 The polyvalent identifier constructor: type, match, builder and instance

We define the constructor macro which acts as a type, a match expander, and a constructor function (which can be called to create a tagged value, i.e. a constructor instance). It can also be directly given a value to directly produce a tagged value, i.e. a constructor instance.

«constructor» ::=

(define-multi-id constructor
  #:type-expander  (make-rest-transformer «type-expander»)
  #:match-expander (make-rest-transformer «match-expander»)
  #:call           (make-rest-transformer «call-expander»))

The constructor? macro returns a predicate for the given constructor name, or checks if a value is an instance of the given constructor name. This form is implemented in «predicate» below.

«constructor?» ::=

(define-syntax constructor? (make-rest-transformer «predicate»))

B.8.3 Type-expander

The type-expander for constructor expects:

The constructor’s tag name, as defined for the tagged call expander in «name-id-mixin»:
«name-id-mixin» ::=
(define-eh-alternative-mixin name-id-mixin
(pattern
(~once (~order-point name-order-point name:id))))
An optional list of type variables, as defined for the tagged call expander in «∀-mixin»:
«∀-mixin» ::=
(define-eh-alternative-mixin ∀-mixin
(pattern {~optional (~seq #:∀ ({~named-seq tvarᵢ :id …})
(~global-or tvars?))}))

An optional list of types:

«constructor-type-types-mixin» ::=

(define-eh-alternative-mixin types-mixin
  (pattern
   (~maybe/empty (~after name-order-point «name-after-field-error»
                         τᵢ:type … {~lift-rest τ-rest}))))

The three elements can appear in any order, with one constraint: the name must appear before the first type. Not only does it make more sense semantically, but it also avoids ambiguities when some of the types are plain type identifiers.

«name-after-field-error» ::=

"The name must appear before any value or type"

«constructor-type-args-mixin» ::=

(define-eh-alternative-mixin constructor-type-seq-args-mixin
  #:define-syntax-class constructor-type-seq-args-syntax-class
  (pattern {~mixin name-id-mixin})
  (pattern {~mixin types-mixin})
  (pattern {~mixin ∀-mixin}))

The type expander handles two cases: when type variables are present, it uses the low-level function tagged-∀-type!, otherwise it uses the low-level function tagged-type!. The constructor contains a (possibly improper) list of values. The type of that list is expressed using the syntax of the xlist library.

«type-expander» ::=

(λ/syntax-parse :constructor-type-seq-args-syntax-class
  (if (attribute tvars?)
      (tagged-∀-type! #'((tvarᵢ …) name [values (xlist τᵢ … . τ-rest)]))
      (tagged-type! #'(name [values (xlist τᵢ … . τ-rest)]))))

B.8.4 Match-expander

«match-expander» ::=

(syntax-parser
[(name:id . pats)
(tagged-match! #'(name [values (xlist . pats)]))])

The match expander simply matches the given patterns against the constructor’s single field, values. The patterns will usually match one value each, but the xlist pattern expander allows a more flexible syntax than the regular list match pattern.

B.8.5 Predicate

The constructor? macro expands to a predicate and accepts the same syntax as for the type expander, without polymorphic variables. Additionally the resulting type as expanded by xlist must be a suitable argument to make-predicate.

«predicate» ::=

(λ/syntax-parse (name:id . types)
(tagged-predicate! #'(name [values (xList . types)])))

B.8.6 Instance creation

The constructor macro can return a builder function or an instance. It accepts the following syntaxes:

(constructor name *), which returns a polymorphic builder function that infers the type of its arguments. All arguments are aggregated into a list with the inferred type for each element, and that list is used as the constructor’s value.

«infer-pat» ::=

(~after name-order-point «name-after-field-error»
{~literal *})

«call-expander-cases»1 ::=

[(~no-order {~mixin ∀-mixin} {~mixin name-id-mixin} {~once «infer-pat»})
#`(… (λ #:∀ (A ...) [l : A ... A]
(#,(tagged-builder! #'(… (name [values (List A ... A)])))
l)))]

(constructor : τᵢ …), which returns a builder function. This does not support the extended xlist syntax, as Typed/Racket’s function types are not expressive enough to support it.

«colon-pat» ::=

(~after name-order-point «name-after-field-error»
:colon τᵢ …
{~lift-rest {~and τ-rest ()}})

«call-expander-cases»2 ::=

[(~no-order {~mixin ∀-mixin} {~mixin name-id-mixin} {~once «colon-pat»})
(define-temp-ids "~a/arg" (τᵢ …))
#`(λ #,@(when-attr tvars? #'(#:∀ (tvarᵢ …))) ([τᵢ/arg : τᵢ] …)
(#,(tagged-builder! #'(name [values (List τᵢ …)]))
(list τᵢ/arg …)))]

(constructor. (! . xlist-type)), which returns a builder function expecting the values as a rest argument, and casts the list at runtime. The xlist-type must be a valid sequence of types for the type form of xlist, and the result must be a suitable argument to make-predicate.

«!-pat» ::=

(~after name-order-point «name-after-field-error»
{~datum !} τᵢ … {~lift-rest τ-rest})

«call-expander-cases»3 ::=

[(~no-order {~mixin ∀-mixin} {~mixin name-id-mixin} {~once «!-pat»})
#`(λ [l : Any *]
(#,(tagged-builder! #'(name [values (xList τᵢ … . τ-rest)]))
(cast l (xlist τᵢ … . τ-rest))))]

(constructor. (:: . xlist-type)), which returns a builder function expecting the whole list of values as a single argument, and returns the constructor instance containing that list. The xlist-type must be a valid sequence of types for the type form of xlist.

«dcolon-pat» ::=

(~after name-order-point «name-after-field-error»
{~datum ::} τᵢ … {~lift-rest τ-rest})

«call-expander-cases»4 ::=

[(~no-order {~mixin ∀-mixin} {~mixin name-id-mixin} {~once «dcolon-pat»})
(if (attribute tvars?)
     (tagged-builder!   #'(name
                           [values (xlist τᵢ … . τ-rest)]))
     (tagged-∀-builder! #'((tvarᵢ …)
                           name
                           [values (xList τᵢ … . τ-rest)])))]

(constructor. (value-maybe-typeᵢ. (… . rest))), which returns an instance containing a (possibly improper) list with the given values and rest as the tail of the list. If rest is (), then the result is a proper list.

«call-expander-cases»5 ::=

[(~no-order {~mixin ∀-mixin}
            {~mixin name-id-mixin}
            (~maybe/empty
             (~after name-order-point «name-after-field-error»
                     :value-maybe-type …
                     «call-expander-rest»)))
(define-temp-ids "~a/arg" (τᵢ …))
(quasitemplate
  (#,(tagged-∀-builder! #'((tvarᵢ … tvarₖ … … tvar-rest …)
                           name
                           [values (xlist τᵢ … #:rest x-τ-rest)]))
   (list* {?? (ann vᵢ aᵢ) vᵢ}
          …
          {?? (ann v-rest a-rest) v-rest})))]

Each value-maybe-typeᵢ may be one of:

[valᵢ : τᵢ]
[: τᵢ valᵢ]
valᵢ

«value-maybe-type» ::=

(define-syntax-class value-maybe-type
  (pattern [vᵢ :colon τᵢ:type] #:with aᵢ #'τᵢ #:with (tvarₖ …) #'())
  (pattern [:colon τᵢ:type vᵢ] #:with aᵢ #'τᵢ #:with (tvarₖ …) #'())
  (pattern vᵢ:literal-value
           #:with τᵢ #'vᵢ.type
           #:with aᵢ #'vᵢ.type
           #:with (tvarₖ …) #'())
  (pattern (~and vᵢ (~not #:rest))
           #:with τᵢ (gensym 'τ)
           #:attr aᵢ #f
           #:with (tvarₖ …) #'(τᵢ)))

Literals are specially recognised so that their type is preserved with as much precision as possible:

«literal-value» ::=

(define-syntax-class literal-value
  (pattern n:number             #:with type #'n)
  (pattern s:str                #:with type #'s)
  (pattern b:boolean            #:with type #'b)
  (pattern c:char               #:with type #'Char)
  (pattern ((~literal quote) v) #:with type (replace-chars #'v))
  (pattern v
           #:when (vector? (syntax-e #'v))
           #:with type (replace-chars #'v)))

As noted in Typed/Racket bug #434, literal characters are not currently recognised as belonging to their own singleton type. We therefore rewrite the type for quoted data to turn literal characters into the Char type:

«replace-chars» ::=

;https://github.com/racket/typed-racket/issues/434
(define (replace-chars t)
  (cond [(syntax? t)  (datum->syntax t
                                     (replace-chars (syntax-e t))
                                     t
                                     t)]
        [(pair? t)    (list 'Pairof
                            (replace-chars (car t))
                            (replace-chars (cdr t)))]
        [(char? t)    'Char]
        [(vector? t)  (cons 'Vector (map replace-chars
                                         (vector->list t)))]
        [(null? t)    'Null]
        [(number? t)  t]
        [(string? t)  t]
        [(boolean? t) t]
        ;Hope for the best.
        ;We really should use a ∀ tvar instead.
        [else         (list 'quote t)]))

Optionally, a rest element may be specified using the following syntax: «call-expander-rest» ::=

(~either «call-expander-rest-keyword»
«call-expander-empty-rest»
«call-expander-dotted-rest»)

«call-expander-rest-keyword» ::=

(~as-rest #:rest
          ;pattern for the value, infers type for literals
          (~either (~and v-rest:literal-value
                         {~with a-rest #'v-rest.type})
                   (~and v-rest
                         {~attr a-rest #f}))
          (~either (~and {~seq}
                         {~with x-τ-rest      (gensym 'x-τ-rest)}
                         {~with (tvar-rest …) #'(x-τ-rest)})
                   (~and (~seq :colon x-τ-rest)
                         {~with (tvar-rest …) #'()})))

«call-expander-empty-rest» ::=

(~seq
(~lift-rest
  (~and ()
        {~with v-rest        #'null}
        {~with a-rest        #'Null}
        {~with x-τ-rest      #'Null}
        {~with (tvar-rest …) #'()})))

«call-expander-dotted-rest» ::=

(~seq
(~lift-rest
  (~either (~and v-rest:type-label
                 (~with x-τ-rest      #'v-rest.type)
                 {~with a-rest        #'v-rest.type}
                 (~with (tvar-rest …) #'()))
           (~and v-rest:literal-value
                 (~with x-τ-rest      #'v-rest.type)
                 {~with a-rest        #'v-rest.type}
                 (~with (tvar-rest …) #'()))
           (~and v-rest
                 (~with x-τ-rest      (gensym 'x-τ-rest))
                 {~attr a-rest        #f}
                 (~with (tvar-rest …) #'(x-τ-rest))))))

The last case depends on the type-label? syntax class to recognise uses of the #{val : type} type annotation syntax from typed/racket. Typed/Racket enables that reader extension, which embeds the type into the value as a syntax property for later use by the type checker

«type-label-syntax-class» ::=

(define-syntax-class type-label
  #:attributes (type raw-type)
  (pattern v
           #:attr raw-type (syntax-property #'v-rest 'type-label)
           #:when (attribute raw-type)
           #:attr type     (datum->syntax #'v-rest
                                          (attribute raw-type)
                                          #'v-rest)))

All four forms accept a #:∀ (tvarᵢ …) specification, and the fourth injects a tvarᵢ type variable for values for which no type is given.

«call-expander» ::=

(syntax-parser
«call-expander-cases»)

B.8.7 Defining shorthands for constructors with define-constructor

The define-constructor macro binds an identifier to a type-expander, match-expander and call-expander for the constructor with the same name. It also defines a predicate for that constructor type.

Like define-tagged, the constructor macro expects:

The tagged structure’s tag name, as defined for the call expander in «name-id-mixin»
An optional list of type variables, as defined for the call expander in «∀-mixin»
Optionally, the tag name to be used, specified with #:tag tag-name as for define-tagged in Defining shorthands with define-tagged:
«tag-kw-mixin» ::=
(define-eh-alternative-mixin tag-kw-mixin
(pattern {~optional {~seq #:tag explicit-tag «default-tag-name»}}))
The tag name defaults to name, i.e. the identifier currently being defined.
«default-tag-name» ::=
{~post-check
{~bind [tag-name (or (attribute explicit-tag)
#'name)]}}
Optionally, a name for the predicate, specified with #:? predicate-name? as for define-tagged in Defining shorthands with define-tagged:
«predicate?-mixin» ::=
(define-eh-alternative-mixin predicate?-mixin
(pattern {~optional {~seq #:? predicate? «default-name?»}}))
The predicate name defaults to name?, where name is the identifier currently being defined.
«default-name?» ::=
{~post-check
{~bind [name? (or (attribute predicate?)
(format-id/record #'name "~a?" #'name))]}}

Unlike define-tagged, which also expects a list of field names possibly annotated with a type, the constructor macro instead expects a description of the list of values it contains. Three syntaxes are accepted:

(colon-pat) ::=
(~after name-order-point «name-after-field-error»
:colon τᵢ …
{~lift-rest {~and τ-rest ()}})
(!-pat) ::=
(~after name-order-point «name-after-field-error»
{~datum !} τᵢ … {~lift-rest τ-rest})
(dcolon-pat) ::=
(~after name-order-point «name-after-field-error»
{~datum ::} τᵢ … {~lift-rest τ-rest})

These syntaxes control how the call expander for the defined name works, and have the same meaning as in the call expander for constructor (xlist, cast and single-argument xlist).

«define-constructor» ::=

(define-syntax define-constructor
  (syntax-parser-with-arrows
   [(_ . (~no-order {~mixin name-id-mixin}
                    {~mixin ∀-mixin}
                    {~mixin tag-kw-mixin}
                    {~mixin predicate?-mixin}
                    (~once
                     (~and (~seq type-decls …)
                           (~either «colon-pat»
                                    «!-pat»
                                    «dcolon-pat»)))))
    #:with tvarᵢ→Any (stx-map (const #'Any) #'(tvarᵢ …))
    «normalize-type/define»
    (quasisyntax/top-loc stx
      (begin
        «multi-id/define»
        «predicate/define»))]))

«multi-id/define» ::=

(define-multi-id name
  #:type-expander  (make-id+call-transformer «type-expander/define»)
  #:match-expander (make-rest-transformer    «match-expander/define»)
  #:else                                     «call-expander/define»)

«type-expander/define» ::=

#'(constructor tag-name
#,@(when-attr tvars? #'(#:∀ (tvarᵢ …)))
τᵢ … . τ-rest)

«call-expander/define» ::=

#'(constructor tag-name
#,@(when-attr tvars? #'(#:∀ (tvarᵢ …)))
type-decls …)

In order to attach patterns to the xlist type, pre-process the types using normalize-xlist-type.

«normalize-type/define»1 ::=

#:with «with-normalize» (normalize-xlist-type #'(τᵢ … . τ-rest) stx)

Once normalized, the types for the xlist are all of the form τᵢ ^ {repeat …}, except for the rest type, which is always present including when it is Null, and is specified using #:rest rest-type.

«with-normalize» ::=

({~seq normalized-τᵢ {~literal ^} (normalized-repeat …)} …
#:rest normalized-rest)

We then define an argument for the pattern expander corresponding to each type within the normalized sequence:

«normalize-type/define»2 ::=

(define-temp-ids "~a/pat" (normalized-τᵢ …))

The match expander expects these patterns and a rest pattern:

«match-expander/define» ::=

(syntax-parser
[({~var normalized-τᵢ/pat} … . {~either «match-rest-signature/define»})
#'#,(tagged-match! #'(name [values «match-xlist/define»]))])

The rest pattern can be specified either using a dotted notation if it is a single term, using #:rest pat-rest, or can be omitted in which case it defaults to matching null. The following syntaxes are therefore accepted:

«match-rest-signature/define» ::=

(#:rest pat-rest)
(~and () {~bind [pat-rest #'(? null?)]})
pat-rest:not-stx-pair

The match expander produces an xlist pattern using the given patterns and the optional rest pattern. The given patterns are repeated as within the type specification.

«match-xlist/define» ::=

(and (? (make-predicate (xlist τᵢ … . τ-rest)))
(split-xlist (list normalized-τᵢ/pat … pat-rest)
τᵢ … . τ-rest))

«predicate/define» ::=

(define name?
  #,(if (attribute tvars?)
        (tagged-predicate!
         #'(tag-name [values ((xlist τᵢ … . τ-rest) tvarᵢ→Any)]))
        (tagged-predicate!
         #'(tag-name [values (xlist τᵢ … . τ-rest)]))))

B.8.8 Miscellanea

«constructor-values» ::=

(define-syntax constructor-values
(make-id+call-transformer-delayed
(λ () #'(λ-tagged-get-field values))))

«ConstructorTop?» ::=

(define-syntax ConstructorTop?
  (make-id+call-transformer-delayed
   (λ ()
     #`(struct-predicate
        #,(check-remembered-common!
           #'(always-remembered values))))))

«ConstructorTop» ::=

(define-type-expander (ConstructorTop stx)
  (syntax-case stx ()
    [id
     (identifier? #'id)
     #'((check-remembered-common!
         #'(always-remembered values))
        Any)]))

B.8.9 Putting it all together

«*» ::=

(require phc-toolkit
         "tagged.hl.rkt"
         "tagged-structure-low-level.hl.rkt"
         (only-in match-string [append match-append])
         type-expander
         xlist
         multi-id
         (for-syntax racket/base
                     syntax/parse
                     syntax/parse/experimental/template
                     racket/contract
                     racket/syntax
                     racket/string
                     racket/function
                     racket/list
                     type-expander/expander
                     phc-toolkit/untyped
                     extensible-parser-specifications))

(provide constructor-values
         constructor
         constructor?
         ConstructorTop
         ConstructorTop?
         define-constructor
         (for-syntax constructor-type-seq-args-syntax-class))

(begin-for-syntax
  (define-syntax-class not-stx-pair
    (pattern {~not (_ . _)}))
  «type-label-syntax-class»
  «name-id-mixin»
  «∀-mixin»
  «constructor-type-types-mixin»
  «constructor-type-args-mixin»
  «tag-kw-mixin»
  «predicate?-mixin»
  «replace-chars»
  «literal-value»
  «value-maybe-type»)

«constructor»
«constructor?»
«ConstructorTop»
«ConstructorTop?»
«define-constructor»
«constructor-values»

B.9 User API for variants

B.9.1 Introduction

B.9.2 Implementation of variant

B.9.3 Predicate

B.9.4 define-variant

B.9.5 Conclusion

B.9.1 Introduction

For convenience, we write a variant form, which is a thin wrapper against (U (~or constructor tagged) …).

B.9.2 Implementation of variant

In define-variant, we only define the type (which is the union of all the possible constructors. We do not bind identifiers for the constructors, for two reasons: the same constructors could appear in several variants, so we would define them twice, and it is likely that a constructor will have the same identifier as an existing variable or function.

«constructor-or-tagged-stx-class» ::=

(begin-for-syntax
  (define-syntax-class constructor-or-tagged
    (pattern [constructor-name:id . (~or ([field:id C:colon type:expr] …)
                                         (type:expr …))])))

«variant» ::=

(define-type-expander (variant stx)
  (syntax-parse stx
    [(_ :constructor-or-tagged …)
     (template
      (U (?? (tagged constructor-name [field C type] …)
             (constructor constructor-name type …))
         …))]))

B.9.3 Predicate

«variant?» ::=

(define-syntax/parse (variant? :constructor-or-tagged …)
  (template
   (λ (v) (or (?? ((tagged? constructor-name field …) v)
                  (constructor? constructor-name v))
              …))))

B.9.4 define-variant

«define-variant» ::=

(define-syntax/parse
    (define-variant variant-name
      (~optkw #:debug)
      (~maybe #:? name?)
      (~maybe #:match variant-match)
      (~and constructor-or-tagged :constructor-or-tagged) …)
  (define/with-syntax default-name? (format-id #'name "~a?" #'name))
  (define/with-syntax default-match (format-id #'name "~a-match" #'name))
  (define-temp-ids "pat" ((type …) …))
  (define-temp-ids "match-body" (constructor-name …))
  (template
   (begin
     (define-type variant-name
       (variant [constructor-name (?? (?@ [field C type] …)
                                      (?@ type …))]
                …))
     (define-syntax (?? variant-match default-match)
       (syntax-rules (constructor-name … (?? (?@ field …)) …)
         [(_ v
             [(constructor-name (?? (?@ [field pat] …)
                                    (pat …)))
              . match-body]
             …)
          (match v
            (?? [(tagged constructor-name [field pat] …) . match-body]
                [(constructor constructor-name pat …) . match-body])
            …)]))
     (define-multi-id (?? name? default-name?)
       #:else
       #'(variant? constructor-or-tagged …)))))

B.9.5 Conclusion

«*» ::=

(require (for-syntax racket/base
                     racket/list
                     syntax/parse
                     syntax/parse/experimental/template
                     racket/syntax
                     phc-toolkit/untyped
                     type-expander/expander)
         phc-toolkit
         multi-id
         type-expander
         "constructor.hl.rkt"
         "structure.hl.rkt")

(provide variant
         variant?
         define-variant)

«constructor-or-tagged-stx-class»
«variant»
«variant?»
«define-variant»

B.10 Somewhat outdated overview of the implementation choices for structures, graphs and passes

B.10.1 Structures

Structures are represented as lists of key/value pairs. We need lists and can't use vectors (or hash tables) because the latter are mutable in typed/racket, and the typing system has no guarantee that accessing the same element twice will yield the same value (so occurence typing can't narrow the type in branches of conditionnals). Actually, we can use structs (they are immutable by default, and the occurrence typing knows that). There are two problems with them. The first problem is that we cannot have subtyping (although knowing all the structs used in the program means we can just filter them and use a (U S1 S2 …). The second problem is that in order to declare the structs, we would need to be in a define-like environment (therefore making anonymous structure types problematic). The second problem can be solved in the same way as the first: if all the structs are known in advance, we can pre-declare them in a shared file.

«example-simple-structure» ::=

(define-type abc (List (Pairof 'a Number)
                       (Pairof 'b String)
                       (Pairof 'c (U 'x 'y))))

(: make-abc (→ Number String (U 'x 'y) abc))
(define (make-abc a b c)
  (list (cons 'a a) (cons 'b b) (cons 'c c)))
(make-abc 1 "b" 'x)

Occurrence typing works:

«example-simple-structure-occurrence» ::=

(: f (→ abc (U 'x #f)))
(define (f v)
  (if (eq? 'x (cdr (cddr v)))
      (cdr (cddr v))
      #f))

B.10.2 Passes, subtyping and tests

Below is the definition of a function which works on (structure [a Number] [b String] [c Boolean]), and returns the same structure extended with a field [d Number], but is only concerned with fields a and c, so tests don’t need to provide a value for b.

«example-pass-which-extends-input»1 ::=

(: pass-calc-d (∀ (TB) (→ (List (Pairof 'a Number)
                                (Pairof 'b TB)
                                (Pairof 'c Boolean))
                          (List (Pairof 'a Number)
                                (Pairof 'b TB)
                                (Pairof 'c Boolean)
                                (Pairof 'd Number)))))
(define (pass-calc-d v)
  (list (car v) ; a
        (cadr v) ; b
        (caddr v) ; c
        (cons 'd (+ (cdar v) (if (cdaddr v) 0 1)))))

The example above can be called to test it with a dummy value for b:

«example-pass-which-extends-input»2 ::=

(pass-calc-d '((a . 1) (b . no-field) (c . #t)))

But when called with a proper value for b, we get back the original string as expected, and the type is correct:

«example-pass-which-extends-input»3 ::=

(ann (pass-calc-d '((a . 1) (b . "some string") (c . #t)))
     (List (Pairof 'a Number)
           (Pairof 'b String)
           (Pairof 'c Boolean)
           (Pairof 'd Number)))

If the pass should be able to work on multiple graph types (each being a subtype containing a common subset of fields), then it should be easy to mark it as a case→ function. It is probably better to avoid too permissive subtyping, otherwise, imagine we have a pass which removes Additions and Substractions from an AST, and replaces them with a single Arithmetic node type. If we have full duck typing, we could call it with Additions and Substraction hidden in fields it does not know about, and so it would fail to replace them. Also, it could be called with an already-processed AST which already contains just Arithmetic node types, which would be a bug most likely. Therefore, explicitly specifying the graph type on which the passes work seems a good practice. Some parts can be collapsed easily into a ∀ type T, when we’re sure there shouldn’t be anything that interests us there.

B.10.3 Graphs

In order to be able to have cycles, while preserving the benefits of occurrence typing, we need to make sure that from the type system’s point of view, accessing a successor node twice will return the same value each time.

The easiest way for achieving this is to wrap the to-be-created value inside a Promise. Occurrence typing works on those:

«test-promise-occurence-typing» ::=

(: test-promise-occurence (→ (Promise (U 'a 'b)) (U 'a #f)))
(define (test-promise-occurence p)
  (if (eq? (force p) 'a)
      (force p)
      #f))

B.10.4 Conclusion

«*» ::=

«example-simple-structure»
«example-simple-structure-occurrence»

«example-pass-which-extends-input»

«test-promise-occurence-typing»

C Implementation of Remember

C.1 remember

This module allows macros to remember some values across compilations. Values are stored within the remembered-values hash table, which associates a category (a symbol) with a set of values.

«remembered-values»1 ::=

(begin-for-syntax
(define remembered-values (make-hash)))

A second set tracks values which were recently written, but not initially added via remembered! or remembered-add!.

«remembered-values»2 ::=

(begin-for-syntax
(define written-values (make-hash)))

The user can specify input files from which remembered values are loaded, and optionally an output file to which new, not-yet-remembered values will be appended:

«remember-file» ::=

(define-for-syntax remember-output-file-parameter
  (make-parameter #f (or? path-string? false?)))

(define-syntax (remember-output-file stx)
  (syntax-case stx ()
    [(_ new-value)
     (string? (syntax-e #'new-value))
     (begin (remember-output-file-parameter (syntax-e #'new-value))
            #'(void))]
    [(_)
     (quasisyntax/loc stx remember-output-file-parameter)]))

(define-syntax (remember-input-file stx)
  (syntax-case stx ()
    [(_ name)
     (string? (syntax-e #'name))
     #'(require (only-in name))]))

(define-syntax-rule (remember-io-file name)
  (begin (remember-input-file name)
         (remember-output-file name)))

«remember» ::=

(define-syntax-rule (remembered! category value)
  (begin-for-syntax
    (remembered-add! 'category 'value)))

(define-for-syntax writable?
  (disjoin number?
           string?
           symbol?
           char?
           null?
           (λ (v) (and (pair? v)
                       (writable? (car v))
                       (writable? (cdr v))))
           (λ (v) (and (vector? v)
                       (andmap writable? (vector->list v))))))

(define-for-syntax (remembered-add! category value)
  (unless (writable? value)
    (error "Value to remember does not seem to be safely writable:"
           value))
  (unless (symbol? category)
    (error (format "The category was not a symbol, when remembering ~a:"
                   value)
           category))
  (hash-update! remembered-values
                category
                (λ (s) (set-add s value))
                set))

(define-for-syntax (remembered-add-written! category value)
  (unless (writable? value)
    (error "Value to remember does not seem to be safely writable:"
           value))
  (unless (symbol? category)
    (error (format "The category was not a symbol, when remembering ~a:"
                   value)
           category))
  (hash-update! written-values
                category
                (λ (s) (set-add s value))
                set))

(define-for-syntax (remembered? category value)
  (unless (writable? value)
    (error "Value to remember does not seem to be safely writable:"
           value))
  (set-member? (hash-ref remembered-values category set) value))

(define-for-syntax (written? category value)
  (unless (writable? value)
    (error "Value to remember does not seem to be safely writable:"
           value))
  (set-member? (hash-ref written-values category set) value))

(define-for-syntax (remembered-or-written? category value)
  (or (remembered? category value)
      (written? category value)))

(define-for-syntax (remember-write! category value)
  (unless (writable? value)
    (error "Value to remember does not seem to be safely writable:"
           value))
  (unless (or (remembered? category value)
              (written? category value))
    (when (remember-output-file-parameter)
      (with-output-file [port (remember-output-file-parameter)]
        #:exists 'append
        (writeln (list 'remembered! category value)
                 port)))
    (remembered-add-written! category value)))

«delayed-errors» ::=

(begin-for-syntax
(define remember-errors-list '())
(define remember-lifted-error #f))

«error» ::=

(define-for-syntax (remembered-error! category
                                      stx-value
                                      [stx-errs (list stx-value)])
  (set! remember-errors-list
        (cons (list category stx-value stx-errs) remember-errors-list))

  (unless (disable-remember-immediate-error)
    (if (not (syntax-local-lift-context))
        ;; Trigger the error right now
        (remember-all-hard-error)
        ;; Lift a delayed error, which will be triggered later on
        (lift-maybe-delayed-errors))))

(define-for-syntax (remembered-add-error! category stx-value)
  (remembered-add! category (syntax-e stx-value))
  (remembered-error! category stx-value))

«remember-all-hard-error» ::=

;; These two functions allow us to wait around 1000 levels of nested
;; macro-expansion before triggering the error.
;; If the error is triggered immediately when the lifted statements are
;; added at the end of the module, then it can get executed before macros
;; used in the righ-hand side of a (define …) are expanded, for example.
;; Since these macros may need to remember more values, it's better to
;; wait until they are all expanded.
;; The number 1000 above in #‘(delay-remember-all-hard-error1 1000) is
;; arbitrary, but should be enough for most practical purposes, worst
;; case the file would require a few more compilations to settle.
(define-syntax (delay-remember-all-hard-error1 stx)
  (syntax-case stx ()
    [(_ n)
     (number? (syntax-e #'n))
     (if (> (syntax-e #'n) 0)
         #`(let ()
             (define blob
               (delay-remember-all-hard-error2 #,(- (syntax-e #'n) 1)))
             (void))
         (begin (syntax-local-lift-module-end-declaration
                 #`(remember-all-hard-error-macro))
                #'(void)))]))

(define-syntax (delay-remember-all-hard-error2 stx)
  (syntax-case stx ()
    [(_ n)
     (number? (syntax-e #'n))
     (begin
       (syntax-local-lift-module-end-declaration
        #'(delay-remember-all-hard-error1 n))
       #'n)]))

(define-for-syntax (remember-all-hard-error)
  (define remember-errors-list-orig remember-errors-list)
  (set! remember-errors-list '())
  (unless (empty? remember-errors-list-orig)
    (raise-syntax-error
     'remember
     (format (~a "The values ~a were not remembered."
                 " Some of them may have been added to the"
                 " appropriate list automatically."
                 " Please recompile this file now.")
             (string-join (remove-duplicates
                           (reverse
                            (stx-map (compose ~a syntax->datum)
                                     (map cadr
                                          remember-errors-list-orig))))
                          ", "))
     #f
     #f
     (remove-duplicates
      (append-map caddr remember-errors-list-orig)
      #:key (λ (e)
              (cons (syntax->datum e)
                    (build-source-location-list e)))))))
(define-syntax (remember-all-hard-error-macro stx)
  (remember-all-hard-error)
  #'(void))

The disable-remember-immediate-error parameter allows code to temporarily prevent remembered-error! from lifting a delayed error. This can be useful for example when calling remembered-error! from a context where (syntax-local-lift-context) is #false, e.g. outside of the expansion of a macro, but within a begin-for-syntax block.

«disable-remember-errors» ::=

(define-for-syntax disable-remember-immediate-error (make-parameter #f))

The error is still put aside, so that if a delayed error was triggered by another call to remembered-error!, the error will still be included with the other delayed errors. If no delayed error is triggered during macro-expansion, the error that was put aside will be ignored. To prevent that, the user can call lift-maybe-delayed-errors within a context where lifts are possible.

«lift-maybe-delayed-errors» ::=

(define-for-syntax (lift-maybe-delayed-errors)
  (if (syntax-transforming-module-expression?)
      ;; Lift a delayed error, attempting to allow several (1000) levels
      ;; of nested let blocks to expand before pulling the alarm signal.
      (unless remember-lifted-error
        (set! remember-lifted-error #t)
        (syntax-local-lift-module-end-declaration
         #`(delay-remember-all-hard-error1 1000)))
      ;; Lift a delayed error, which will be triggered after the current
      ;; expansion pass (i.e. before the contents of any let form is
      ;; expanded).
      (syntax-local-lift-expression
       #`(remember-all-hard-error-macro))))

«get-remembered» ::=

(define-for-syntax (get-remembered category)
(hash-ref remembered-values category set))

«provide» ::=

(begin-for-syntax
  (provide get-remembered
           remembered-add!
           remembered?
           remembered-or-written?
           remember-write!
           remembered-error!
           remember-output-file-parameter
           disable-remember-immediate-error
           lift-maybe-delayed-errors))
(provide remember-input-file
         remember-output-file
         remember-io-file
         remembered!)

(module+ private
  (begin-for-syntax
    (provide remembered-add-written!)))

«*» ::=

(require mzlib/etc
         ;; TODO: circumvent https://github.com/racket/scribble/issues/44
         racket/require
         (subtract-in phc-toolkit/untyped syntax/stx)
         syntax/stx
         (for-syntax racket/base
                     racket/function
                     racket/bool
                     racket/set
                     racket/list
                     mzlib/etc
                     ;;TODO: https://github.com/racket/scribble/issues/44
                     (subtract-in phc-toolkit/untyped
                                  syntax/stx)
                     syntax/stx
                     syntax/srcloc
                     racket/string
                     racket/format))
«provide»
«remembered-values»
«remember-file»
«remember»
«get-remembered»
«delayed-errors»
«disable-remember-errors»
«lift-maybe-delayed-errors»
«remember-all-hard-error»
«error»

D Implementation of the multi-id library

Suzanne Soy <racket@suzanne.soy>

This document describes the implementation of the multi-id library, using literate programming. For the library’s documentation, see the Polyvalent identifiers with multi-id document instead.

D.1 Syntax properties implemented by the defined multi-id

The multi-id macro defines the identifier name as a struct with several properties:

prop:type-expander, so that the identifier acts as a type expander
«props»1 ::=
(?? (?@ #:property prop:type-expander p-type))
Optionally, the user can request the type to not be expanded, in which case we bind the type expression to a temporary type name, using the original define-type from typed/racket:
«maybe-define-type»1 ::=
(?? (tr:define-type name p-type-noexpand #:omit-define-syntaxes))
The user can otherwise request that the type expression be expanded once and for all. This can be used for performance reasons, to cache the expanded type, instead of re-computing it each time the name identifier is used as a type. To achieve that, we bind the expanded type to a temporary type name using define-type as provided by the type-expander library:
«maybe-define-type»2 ::=
(?? (define-type name p-type-expand-once #:omit-define-syntaxes))
The two keywords #:type-noexpand and #:type-expand-once can also be used to circumvent issues with recursive types (the type expander would otherwise go in an infinite loop while attempting to expand them). This behaviour may be fixed in the future, but these options should stay so that they can still be used for performance reasons.

prop:match-expander, so that the identifier acts as a match expander

«props»2 ::=

(?? (?@ #:property prop:match-expander p-match))
(?? (?@ #:property prop:match-expander
(λ (stx) (syntax-case stx ()
[(_ . rest) #'(p-match-id . rest)]))))

prop:custom-write, so that the identifier can be printed in a special way. Note that this does not affect instances of the data structure defined using multi-id. It is even possible that this property has no effect, as no instances of the structure should ever be created, in practice. This feature is therefore likely to change in the future.
«props»3 ::=
(?? (?@ #:property prop:custom-write p-write))

prop:set!-transformer, so that the identifier can act as a regular macro, as an identifier macro and as a set! transformer.

«props»4 ::=

#:property prop:set!-transformer
(?? p-set!
    (λ (_ stx)
      (syntax-case stx (set!)
        [(set! self . rest) (?? p-set! «fail-set!»)]
        (?? [(_ . rest) p-just-call])
        (?? [_ p-just-id]))))

Any prop:xxx identifier can be defined with #:xxx, if so long as the prop:xxx identifier is a struct-type-property?.
«props»5 ::=
(?@ #:property fallback.prop fallback-value)
…

The multi-id macro therefore defines name as follows:

«multi-id-body» ::=

(template
(begin
   «maybe-define-type»
   (define-syntax name
     (let ()
       (struct tmp ()
         «props»)
       (tmp)))))

D.2 Signature of the multi-id macro

The multi-id macros supports many options, although not all combinations are legal. The groups of options specify how the name identifier behaves as a type expander, match expander, how it is printed with prop:custom-write and how it acts as a prop:set!-transformer, which covers usage as a macro, identifier macro and actual set! transformer.

«multi-id» ::=

(begin-for-syntax
  «stx-class-kw-else»
  «stx-class-kw-set!+call+id»
  «prop-keyword-syntax-class»)
(define-syntax/parse (define-multi-id name:id
                       (~or «type-expander-kws»
                            «match-expander-kws»
                            «custom-write-kw»
                            «set!-transformer-kws»
                            «fallback-kw»)
                       …)
  «multi-id-body»)

These groups of options are detailed below:

The #:type-expander, #:type-noexpand and #:type-expand-once options are mutually exclusive.

«type-expander-kws» ::=

(~optional (~or (~seq #:type-expander p-type:expr)
(~seq #:type-noexpand p-type-noexpand:expr)
(~seq #:type-expand-once p-type-expand-once:expr)))

The #:match-expander and #:match-expander-id options are mutually exclusive.
«match-expander-kws» ::=
(~optional (~or (~seq #:match-expander p-match:expr)
(~seq #:match-expander-id p-match-id:id)))
The #:custom-write keyword can always be used
«custom-write-kw» ::=
(~optional (~seq #:custom-write p-write:expr))

The prop:set!-transformer can be specified as a whole using #:set!-transformer, or using one of #:else, #:else-id, #:mutable-else or #:mutable-else-id, or using some combination of #:set!, #:call (or #:call-id) and #:id.

«set!-transformer-kws» ::=

(~optional (~or (~seq #:set!-transformer p-set!:expr)
:kw-else
:kw-set!+call+id))

More precisely, the kw-else syntax class accepts one of the mutually exclusive options #:else, #:else-id, #:mutable-else and #:mutable-else-id:

«stx-class-kw-else» ::=

(define-splicing-syntax-class kw-else
  #:attributes (p-just-set! p-just-call p-just-id)
  (pattern (~seq #:mutable-else p-else)
           #:with p-just-set! #'#'(set! p-else . rest)
           #:with p-just-call #'#'(p-else . rest)
           #:with p-just-id #'#'p-else)
  (pattern (~seq #:else p-else)
           #:with p-just-set! «fail-set!»
           #:with p-just-call #'#`(#,p-else . rest)
           #:with p-just-id #'p-else)
  (pattern (~seq #:mutable-else-id p-else-id)
           #:with (:kw-else) #'(#:mutable-else #'p-else-id))
  (pattern (~seq #:else-id p-else-id)
           #:with (:kw-else) #'(#:else #'p-else-id)))

The kw-set!+call+id syntax class accepts optionally the #:set! keyword, optionally one of #:call or #:call-id, and optionally the #:id keyword.

«stx-class-kw-set!+call+id» ::=

(define-splicing-syntax-class kw-set!+call+id
  (pattern (~seq (~or
                  (~optional (~seq #:set! p-user-set!:expr))
                  (~optional (~or (~seq #:call p-user-call:expr)
                                  (~seq #:call-id p-user-call-id:id)))
                  (~optional (~or (~seq #:id p-user-id:expr)
                                  (~seq #:id-id p-user-id-id:expr))))
                 …)
           #:attr p-just-set!
           (and (attribute p-user-set!) #'(p-user-set! stx))
           #:attr p-just-call
           (cond [(attribute p-user-call)
                  #'(p-user-call stx)]
                 [(attribute p-user-call-id)
                  #'(syntax-case stx ()
                      [(_ . rest) #'(p-user-call-id . rest)])]
                 [else #f])
           #:attr p-just-id
           (cond [(attribute p-user-id) #'(p-user-id stx)]
                 [(attribute p-user-id-id) #'#'p-user-id-id]
                 [else #f])))

When neither the #:set! option nor #:set!-transformer are given, the name identifier acts as an immutable object, and cannot be used in a set! form. If it appears as the second element of a set! form, it raises a syntax error:

«fail-set!» ::=

#'(raise-syntax-error
'self
(format "can't set ~a" (syntax->datum #'self)))

As a fallback, for any #:xxx keyword, we check whether a corresponding prop:xxx exists, and whether it is a struct-type-property?:

«fallback-kw» ::=

(~seq fallback:prop-keyword fallback-value:expr)

The check is implemented as a syntax class:

«prop-keyword-syntax-class» ::=

(define-syntax-class prop-keyword
  (pattern keyword:keyword
           #:with prop (datum->syntax #'keyword
                                      (string->symbol
                                       (string-append
                                        "prop:"
                                        (keyword->string
                                         (syntax-e #'keyword))))
                                      #'keyword
                                      #'keyword)
           #:when (eval #'(struct-type-property? prop))))

D.3 Tests for multi-id

«test-multi-id»1 ::=

(define (p1 [x : Number]) (+ x 1))

(define-type-expander (Repeat stx)
  (syntax-case stx ()
    [(_ t n) #`(List #,@(map (λ (x) #'t)
                             (range (syntax->datum #'n))))]))

(define-multi-id foo
  #:type-expander
  (λ (stx) #'(List (Repeat Number 3) 'x))
  #:match-expander
  (λ (stx) #'(vector _ _ _))
  #:custom-write
  (λ (self port mode) (display "custom-write for foo" port))
  #:set!-transformer
  (λ (_ stx)
    (syntax-case stx (set!)
      [(set! self . _)
       (raise-syntax-error 'foo (format "can't set ~a"
                                        (syntax->datum #'self)))]
      [(_ . rest) #'(+ . rest)]
      [_ #'p1])))

(check-equal? (ann (ann '((1 2 3) x) foo)
                   (List (List Number Number Number) 'x))
              '((1 2 3) x))

;(set! foo 'bad) should throw an error here

(let ([test-match (λ (val) (match val [(foo) #t] [_ #f]))])
  (check-equal? (test-match #(1 2 3)) #t)
  (check-equal? (test-match '(1 x)) #f))

(check-equal? (foo 2 3) 5)
(check-equal? (map foo '(1 5 3 4 2)) '(2 6 4 5 3))

It would be nice to test the (set! foo 'bad) case, but grabbing the compile-time error is a challenge (one could use eval, but it’s a bit heavy to configure).

Test with #:else:

«test-multi-id»2 ::=

(begin-for-syntax
  (define-values
    (prop:awesome-property awesome-property? get-awesome-property)
    (make-struct-type-property 'awesome-property)))

(define-multi-id bar-id
  #:type-expander
  (λ (stx) #'(List `,(Repeat 'x 2) Number))
  #:match-expander
  (λ (stx) #'(cons _ _))
  #:custom-write
  (λ (self port mode) (display "custom-write for foo" port))
  #:else-id p1
  #:awesome-property 42)

(check-equal? (ann (ann '((x x) 79) bar)
                   (List (List 'x 'x) Number))
              '((x x) 79))

;(set! bar 'bad) should throw an error here

(let ([test-match (λ (val) (match val [(bar-id) #t] [_ #f]))])
  (check-equal? (test-match '(a . b)) #t)
  (check-equal? (test-match #(1 2 3)) #f))

(let ([f-bar-id bar-id])
  (check-equal? (f-bar-id 6) 7))
(check-equal? (bar-id 6) 7)
(check-equal? (map bar-id '(1 5 3 4 2)) '(2 6 4 5 3))

(require (for-syntax rackunit))
(define-syntax (check-awesome-property stx)
  (syntax-case stx ()
    [(_ id val)
    (begin (check-pred awesome-property?
                       (syntax-local-value #'id (λ _ #f)))
           (check-equal? (get-awesome-property
                          (syntax-local-value #'id (λ _ #f)))
                         (syntax-e #'val))
           #'(void))]))
(check-awesome-property bar-id 42)

«test-multi-id»3 ::=

(define-multi-id bar
  #:type-expander
  (λ (stx) #'(List `,(Repeat 'x 2) Number))
  #:match-expander
  (λ (stx) #'(cons _ _))
  #:custom-write
  (λ (self port mode) (display "custom-write for foo" port))
  #:else #'p1)

(check-equal? (ann (ann '((x x) 79) bar)
                   (List (List 'x 'x) Number))
              '((x x) 79))

;(set! bar 'bad) should throw an error here

(let ([test-match (λ (val) (match val [(bar) #t] [_ #f]))])
  (check-equal? (test-match '(a . b)) #t)
  (check-equal? (test-match #(1 2 3)) #f))

(check-equal? (bar 6) 7)
(check-equal? (map bar '(1 5 3 4 2)) '(2 6 4 5 3))

D.4 Conclusion

«*» ::=

(require (only-in type-expander prop:type-expander define-type)
         (only-in typed/racket [define-type tr:define-type])
         phc-toolkit/untyped
         (for-syntax phc-toolkit/untyped
                     racket/base
                     racket/syntax
                     syntax/parse
                     syntax/parse/experimental/template
                     (only-in type-expander prop:type-expander)))
(provide define-multi-id)

«multi-id»

(module* test-syntax racket/base
  (provide tests)
  (define tests #'(begin «test-multi-id»)))

E Type expander: Implementation

Suzanne Soy <racket@suzanne.soy>

This library is implemented using literate programming. The implementation details are presented in the following sections. The user documentation is in the Type expander library document.

E.1 Implementation of the type expander library

E.1.1 Introduction

E.1.2 Expansion model for type expanders

E.1.2.1 Comparison with TeX’s macro expansion model

E.1.2.2 Interactions between type expanders and scopes

E.1.3 The prop:type-expander structure type property

E.1.3.1 The type-expander struct

E.1.4 Associating type expanders to identifiers

E.1.4.1 The type-expander syntax class

E.1.4.2 Calling type expanders

E.1.4.3 Associating type expanders to already existing identifiers

E.1.4.4 Defining new type expanders

E.1.4.5 Locally binding type expanders

E.1.5 Expanding types

E.1.5.1 Cases handled by expand-type

E.1.5.2 Applying type expanders

E.1.5.2.1 Polymorphic types with ∀

E.1.5.2.2 Recursive types with Rec

E.1.5.2.3 Local bindings with Let and Letrec

E.1.5.2.4 Anonymous types with Λ

E.1.5.2.5 Preventing the expansion of types with No-Expand

E.1.5.2.6 The overloaded : identifier

E.1.5.2.7 Last resort cases: leaving the type unchanged

E.1.5.3 Debugging type expanders

E.1.6 Overloading typed/racket forms

E.1.6.1 syntax classes

E.1.6.2 Overview of the overloaded primitives

E.1.6.9 define-struct/exec

E.1.6.18 make-predicate

E.1.6.19 :type, :print-type, :query-type/args, :query-type/result

E.1.6.20 Type expanders for the typed classes

E.1.6.21 Other typed/racket forms

E.1.7 Future work

E.1.8 Conclusion

E.2 Some example type expanders

E.2.1 Example type expanders: quasiquote and quasisyntax

E.2.2 Implementation of the Let* special type expander form

E.2.3 curry

E.2.4 Putting it all together

E.1 Implementation of the type expander library

This document describes the implementation of the type-expander library, using literate programming. For the library’s documentation, see the Type expander library document instead.

E.1.1 Introduction

Extensible types would be a nice feature for typed/racket. Unlike require and provide, which come with define-require-syntax and define-provide-syntax, and unlike match, which comes with define-match-expander, typed/racket doesn’t provide a way to define type expanders. The type-expander library extends typed/racket with the ability to define type expanders, i.e. type-level macros.

The Some example type expanders section presents a small library of type expanders built upon the mechanism implemented here.

We redefine the forms :, define, lambda and so on to equivalents that support type expanders. Type expanders are defined via the define-type-expander macro. Ideally, this would be handled directly by typed/racket, which would directly expand uses of type expanders.

E.1.2 Expansion model for type expanders

Type expanders are expanded similarly to macros, with two minor differences:

A form whose first element is a type expander, e.g. (F . args₁), can expand to the identifier of another type expander G. If the form itself appears as the first element of an outer form, e.g. ((F . args₁) . args₂), the first expansion step will result in (G . args₂). The official macro expander for Racket would then expand G on its own, as an identifier macro, without passing the args₂ to it. In contrast, the type expander will expand the whole (G . args₂) form, letting G manipulate the args₂ arguments.

It is possible to write anonymous macros,

The Λ form can be used to create anonymous type expanders. Anonymous type expanders are to type expanders what anonymous functions are to function definitions. The following table presents the expression-level and type-level function and macro forms. Note that Let serves as a type-level equivalent to both let and let-syntax, as anonymous macros can be used in conjunction with Let to obtain the equivalent of let-syntax.

	Definitions	Local binding	Anonymous functions
Functions	define	let	λ
Macros	define-syntax	let-syntax	N/A
Type‑level functionsa	define-type	Let	∀
Type‑level macros	define-type-expander	Let	Λ

a: The type-level functions are simple substitution functions, and cannot perform any kind of computation. They are, in a sense, closer to pattern macros defined with define-syntax-rule than to actual functions.

Combined, these features allow some form of "curried" application of type expanders: The F type expander could expand to an anonymous Λ type expander which captures the args₁ arguments. In the second expansion step, the Λ anonymous type expander would then consume the args₂ arguments, allowing F to effectively rewrite the two nested forms, instead of being constrained to the innermost form.

E.1.2.1 Comparison with TeX’s macro expansion model

For long-time TeX or LaTeX users, this may raise some concerns. TeX programs are parsed as a stream of tokens. A TeX commands is a macro. When a TeX macro occurs in the stream of tokens, it takes its arguments by consuming a certain number of tokens following it. After consuming these arguments, a TeX macro may expand to another TeX macro, which in turn consumes more arguments. This feature is commonly used in TeX to implement macros which consume a variable number arguments: the macro will initially consume a single argument. Depending on the value of that argument, it will then expand to a macro taking n arguments, or another macro taking m arguments. This pattern, omnipresent in any sufficiently large TeX program, opens the door to an undesirable class of bugs: when a TeX macro invocation appears in the source code, it is not clear syntactically how many arguments it will eventually consume. An incorrect parameter value can easily cause it to consume more arguments than expected. This makes it possible for the macro to consume the end markers of surrounding environments, for example in the code:

\begin{someEnvironment}

\someMacro{arg1}{arg2}

\end{someEnvironment}

the someMacro command may actually expect three arguments, in which case it will consume the \end token, but leave the {someEnvironment} token in the stream. This will result in a badly broken TeX program, which will most likely throw an error complaining that the environment \begin{someEnvironment} is not properly closed. The error may however occur in a completely different location, and may easily cause a cascade of errors (the missing \end{someEnvironment} may cause later TeX commands to be interpreted in a different way, causing them to misinterpret their arguments, which in turn may cause further errors. The end result is a series of mysterious error messages somewhat unrelated to the initial problem.

This problem with TeX macros can be summed up as follows: the number of tokens following a TeX macro invocation that will be consumed by the macro is unbounded, and cannot be easily guessed by looking at the raw source code, despite the presence of programmer-friendly looking syntactic hints, like wrapping arguments with {…}.

We argue that the expansion model for type expanders is less prone to this class of problems, for several reasons:

Firstly, macros can only consume outer forms if they appear as the leftmost leaf of the outer form, i.e. while the F macro in the expression
((F . args₁) . args₂)
may access the args₂ arguments, it will be constrained within the (F . args₁) in the following code:
(H leading-args₂ (F . args₁) . more-args₂)
The first case occurs much more rarely than the second, so is less likely to happen
Secondly, all TeX macros will consume an arbitrary number of arguments in a linear fashion until the end of the enclosing group or a paragraph separation. In contrast, most type expanders will consume all the arguments within their enclosing application form, and no more. “Curried” type expanders, which expand to a lone macro identifier, will likely only represent a small subset of all type expanders. For comparison, consider the following TeX code:
\CommandOne{argA}\CommandTwo{argB}
The \CommandOne TeX macro might consume zero, one, two three or more arguments. If it consumes zero arguments, {argA} will not be interpreted as an argument, but instead will represent a scoped expression, similar to (let () argA). If \CommandOne consumes two or more arguments, \CommandTwo will be passed as an argument, unevaluated, and may be discarded or applied to other arguments than the seemingly obvious {argB} argument. The TeX code above could therefore be equivalent to any the following Racket programs:
(CommandOne)
(let () argA)
(CommandTwo)
(let () argB)
(CommandOne argA)
(CommandTwo)
(let () argB)
(CommandOne)
(let () argA)
(CommandTwo argB)
(CommandOne argA)
(CommandTwo argB)
(CommandOne argA CommandTwo)
(let () argB)
(CommandOne argA CommandTwo argB)
In contrast, the obvious interpretation at a first glance of the TeX program would be written as follows in Racket:
(CommandOne argA)
(CommandTwo argB)
If these appear as “arguments” of a larger expression, then their meaning is unambiguous (unless the larger expression is itself a macro):
(+ (CommandOne argA)
(CommandTwo argB))
If however the (CommandOne argA) is the first element in its form, then, if it is a curried macro, it may consume the the (CommandTwo argB) form too:
((CommandOne argA)
(CommandTwo argB))
As stated earlier, this case will likely be less common, and it is clearer that the intent of the programmer to pass (CommandTwo argB) as arguments to the result of (CommandOne argA), either as a macro application or as a regular run-time function application.
Finally, Racket macros (and type expanders) usually perform a somewhat thorough check of their arguments, using syntax-parse or syntax-case patterns. Arguments to macros and type expanders which do not have the correct shape will trigger an error early, thereby limiting the risk of causing errors in cascade.

E.1.2.2 Interactions between type expanders and scopes

Our expansion model for type expanders therefore allows a type expander to escape the scope in which it was defined before it is actually expanded. For example, the following type:

(Let ([A Number])
  ((Let ([F (Λ (self T)
               #`(Pairof #,(datum->syntax #'self 'A)
                         T))])
     (Let ([A String])
       F))
   A))

first expands to:

(F
A)

and then expands to:

(Pairof String A)

and finally expands to:

(Pairof String A)

Effectively, F captures the scope where its name appears (inside all three Let forms), but is expanded in a different context (outside of the two innermost Let forms).

Using Matthew Flatt’s notation to indicate the scopes present on an identifier, we can more explicitly show the expansion steps:

(Let ([A Number])
  ((Let ([F (Λ (self T)
               #`(Pairof #,(datum->syntax #'self 'A)
                         T))])
     (Let ([A String])
       F))
   A))

The first Let form annotates the identifier it binds with a fresh scope, numbered 1 here, and adds this scope to all identifiers within its body. It stores the binding in the (tl-redirections) binding table, as shown by the comment above the code

;A¹ := Number
((Let¹ ([F¹ (Λ¹ (self¹ T¹)
                #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
                           T¹))])
       (Let¹ ([A¹ String¹])
             F¹))
A¹)

The second Let form then binds the F identifier, adding a fresh scope as before:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
((Let¹² ([A¹² String¹²])
F¹²)
A¹)

The third Let form then binds A within its body, leaving the outer A unchanged:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
;A¹²³ := String¹²
(F¹²³
A¹)

The F¹²³ macro is then expanded, passing as an argument the syntax object #'(F¹²³ A¹). A fresh scope is added to the identifiers generated by the macro, in order to enforce macro hygiene. The A¹ identifier is passed as an input to the macro, so it is left unchanged, and A¹²³ is derived from F¹²³, via datum->syntax, and therefore has the same scopes (F¹²³ is also a macro input, so it is not tagged with the fresh scope). The Pairof¹ identifier, generated by the macro, is however flagged with the fresh scope 4. The result of the application of F to this syntax object is:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
;A¹²³ := String¹²
(Pairof¹⁴ A¹²³ A¹)

The Pairof¹⁴ type is resolved to the primitive type constructor Pairof:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
;A¹²³ := String¹²
(Pairof A¹²³ A¹)

The type A¹²³ is then resolved to String¹², which in turn is resolved to the String built-in type:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
;A¹²³ := String¹²
(Pairof String A¹)

And the type A¹ is resolved to Number:

;A¹ := Number
;F¹² := (Λ¹ (self¹ T¹)
; #`(Pairof¹ #,(datum->syntax¹ #'self¹ 'A¹)
; T¹))
;A¹²³ := String¹²
(Pairof String Number)

The syntax-local-value function does not support querying the transformer binding of identifiers outside of the lexical scope in which they are bound. In our case, however, we need to access the transformer binding of F¹²³ outside of the scope of the Let binding it, and similarly for A¹²³.

E.1.3 The prop:type-expander structure type property

Type expanders are identified by the prop:type-expander structure type property. Structure type properties allow the same identifier to act as a rename transformer, a match expander and a type expander, for example. Such an identifier would have to implement the prop:rename-transformer, prop:match-expander and prop:type-expander properties, respectively.

«prop:type-expander» ::=

(define-values (prop:type-expander
                has-prop:type-expander?
                get-prop:type-expander-value)
  (make-struct-type-property 'type-expander prop-guard))

The value of the prop:type-expander property should either be a transformer procedure of one or two arguments which will be called when expanding the type, or the index of a field containing such a procedure.

«prop-guard» ::=

(define (prop-guard val struct-type-info-list)
  (cond «prop-guard-field-index»
        «prop-guard-procedure»
        «prop-guard-else-error»))

If the value is a field index, it should be within bounds. The make-struct-field-accessor function performs this check, and also returns an accessor. The accessor expects an instance of the struct, and returns the field’s value.

«prop-guard-field-index» ::=

[(exact-nonnegative-integer? val)
(let* ([make-struct-accessor (cadddr struct-type-info-list)]
        [accessor (make-struct-field-accessor make-struct-accessor val)])
   (λ (instance)
     (let ([type-expander (accessor instance)])
       «prop-guard-field-value»)))]

The expander procedure will take one argument: the piece of syntax corresponding to the use of the expander. If the property’s value is a procedure, we therefore check that its arity includes 1.

«prop-guard-field-value» ::=

(cond
  [(and (procedure? type-expander)
        (arity-includes? (procedure-arity type-expander) 2))
   (curry type-expander instance)]
  [(and (procedure? type-expander)
        (arity-includes? (procedure-arity type-expander) 1))
   type-expander]
  [else
   (raise-argument-error 'prop:type-expander-guard
                         (~a "the value of the " val "-th field should"
                             " be a procedure whose arity includes 1 or"
                             " 2")
                         type-expander)])

In the first case, when the property value is a field index, we return an accessor function. The accessor function expects a struct instance, performs some checks and returns the actual type expander procedure.

When the property’s value is directly a type expander procedure, we follow the same convention. We therefore return a function which, given a struct instance, returns the type expander procedure (ignoring the _ argument).

«prop-guard-procedure» ::=

[(procedure? val)
(cond
   [(arity-includes? (procedure-arity val) 2)
    (λ (s) (curry val s))]
   [(arity-includes? (procedure-arity val) 1)
    (λ (_) val)]
   [else
    (raise-argument-error 'prop:type-expander-guard
                          "a procedure whose arity includes 1 or 2"
                          val)])]

When the value of the prop:type-expander property is neither a positive field index nor a procedure, an error is raised:

«prop-guard-else-error» ::=

[else
(raise-argument-error
  'prop:type-expander-guard
  (~a "a procedure whose arity includes 1 or 2, or an exact "
      "non-negative integer designating a field index within "
      "the structure that should contain a procedure whose "
      "arity includes 1 or 2.")
  val)]

E.1.3.1 The type-expander struct

We make a simple struct that implements prop:type-expander and nothing else. It has a single field, expander-proc, which contains the type expander transformer procedure.

«type-expander-struct» ::=

(struct type-expander (expander-proc) #:transparent
#:extra-constructor-name make-type-expander
#:property prop:type-expander (struct-field-index expander-proc))

E.1.4 Associating type expanders to identifiers

E.1.4.1 The type-expander syntax class

The type-expander syntax class recognises identifiers which are bound to type expanders. These fall into three cases:

The identifier’s syntax-local-value is an instance of a struct implementing prop:type-expander
The identifier has been bound by a type-level local binding form like Let or ∀, and therefore are registered in the (tl-redirections) binding table.
The identifier has been patched via patch-type-expander, i.e. a type expander has been globally attached to an existing identifier, in which case the type expander is stored within the patched free identifier table.

«expand-type-syntax-classes» ::=

(define-syntax-class type-expander
  (pattern local-expander:id
           #:when (let ([b (binding-table-find-best (tl-redirections)
                                                    #'local-expander
                                                    #f)])
                    (and b (has-prop:type-expander? b)))
           #:with code #'local-expander)
  (pattern (~var expander
                 (static has-prop:type-expander? "a type expander"))
           #:when (not (binding-table-find-best (tl-redirections)
                                                #'expander
                                                #f))
           #:with code #'expander)
  (pattern patched-expander:id
           #:when (let ([p (free-id-table-ref patched
                                              #'patched-expander
                                              #f)])
                    (and p (has-prop:type-expander? p)))
           #:when (not (binding-table-find-best (tl-redirections)
                                                #'expander
                                                #f))
           #:with code #'patched-expander))

We also define a syntax class which matches types. Since types can bear many complex cases, and can call type expanders which may accept arbitrary syntax, we simply define the type syntax class as expr. Invalid syntax will be eventually caught while expanding the type, and doing a thorough check before any processing would only make the type expander slower, with little actual benefits. The type syntax class is however used in syntax patterns as a form of documentation, to clarify the distinction between types and run-time or compile-time expressions.

«type-syntax-class» ::=

(define-syntax-class type
(pattern :expr))

«type-contract» ::=

(define stx-type/c syntax?)

Finally, we define a convenience syntax class which expands the matched type:

«type-expand-syntax-class» ::=

(define-syntax-class type-expand!
  #:attributes (expanded)
  (pattern t:expr
           #:with expanded (expand-type #'t #f)))

E.1.4.2 Calling type expanders

The apply-type-expander function applies the syntax expander transformer function associated to type-expander-id. It passes stx as the single argument to the transformer function. Usually, stx will be the syntax used to call the type expander, like #'(te arg ...) or just #'te if the type expander is not in the first position of a form.

The identifier type-expander-id should be bound to a type expander, in one of the three possible ways described above.

«apply-type-expander» ::=

(define/contract (apply-type-expander type-expander-id stx)
  (-> identifier? syntax? syntax?)
  (let ([val (or (binding-table-find-best (tl-redirections)
                                          type-expander-id
                                          #f)
                 (let ([slv (syntax-local-value type-expander-id
                                                (λ () #f))])
                   (and (has-prop:type-expander? slv) slv))
                 (free-id-table-ref patched type-expander-id #f))]
        [ctxx (make-syntax-introducer)])
    «apply-type-expander-checks»
    (ctxx (((get-prop:type-expander-value val) val) (ctxx stx)))))

The apply-type-expander function checks that its type-expander-id argument is indeed a type expander before attempting to apply it:

«apply-type-expander-checks» ::=

(unless val
  (raise-syntax-error 'apply-type-expander
                      (format "Can't apply ~a, it is not a type expander"
                              type-expander-id)
                      stx
                      type-expander-id))

E.1.4.3 Associating type expanders to already existing identifiers

As explained above, existing identifiers which are provided by other libraries can be “patched” so that they behave like type expanders, using a global table associating existing identifiers to the corresponding expander code:

«patched» ::=

(define patched (make-free-id-table))

«patch» ::=

(define-syntax patch-type-expander
  (syntax-parser
    [(_ id:id expander-expr:expr)
     #`(begin
         (begin-for-syntax
           (free-id-table-set! patched
                               #'id
                               (type-expander #,(syntax/loc this-syntax
                                                  expander-expr)))))]))

E.1.4.4 Defining new type expanders

The define-type-expander macro binds name to a type expander which uses (λ. ((arg) . body)) as the transformer procedure. To achieve this, we create a transformer binding (with define-syntax), from name to an instance of the type-expander structure.

«define-type-expander» ::=

(define-syntax define-type-expander
  (syntax-parser
    [(_ (name:id arg:id) . body)
     #`(define-syntax name
         (type-expander #,(syntax/loc this-syntax (λ (arg) . body))))]
    [(_ name:id fn:expr)
     #`(define-syntax name
         (type-expander #,(syntax/loc this-syntax fn)))]))

E.1.4.5 Locally binding type expanders

Some features of the type expander need to locally bind new type expanders:

The (Let. (([id expr] …) . body)) special form binds the identifiers id … to the type expanders expr … in its body.
When expanding the body of a (∀ (Tᵢ …) body) form, the Tᵢ bound by the ∀ may shadow some type expanders with the same name. If the ∀ form is directly applied to arguments, each Tᵢ is instead bound to the corresponding argument.
When expanding the body of a (Rec T body) form, the T bound by the Rec may shadow a type expander with the same name.

We use with-bindings (defined in another file) to achieve this. The code

(with-bindings [bound-ids transformer-values]
rebind-stx
transformer-body)

evaluates transformer-body in the transformer environment. It creates a fresh scope, which it applies to the bound-ids and the rebind-stx. It associates each modified bound-id with the corresponding transformer-value in the (tl-redirections) binding table. The with-bindings form does not mutate the syntax objects, instead it shadows the syntax pattern variables mentioned in bound-ids and rebind-stx with versions pointing to the same syntax objects, but with the fresh scope flipped on them.

The code

(with-rec-bindings [bound-ids generate-transformer-values rhs]
rebind-stx
transformer-body)

works in the same way, but it also flips the fresh scope on each element of rhs. The generate-transformer-values is expected to be a transformer expression which, given an element of rhs with the flipped scope, produces the transformer value to bind to the corresponding bound-id.

The implementation of with-bindings unfortunately does not play well with syntax-local-value, so the binding table has to be queried directly instead of using syntax-local-value. To our knowledge, the only ways to make new bindings recognised by syntax-local-value are:

To expand to a define-syntax form, followed with a macro performing the remaining work
Equivalently, to expand to a let-syntax form, whose body is a macro performing the remaining work
To call local-expand with an internal definition context which contains the desired bindings
To explicitly call syntax-local-value with an internal definition context argument

It is not practical in our case to use the first solution involving define-syntax, as the type expander may be called while expanding an expression (e.g. ann). The next two solutions assume that syntax-local-value will be called in a well-scoped fashion (in the sense of the official expander): in the second solution, syntax-local-value must be called by expansion-time code located within the scope of the let-syntax form, and in the third solution, syntax-local-value must be called within the dynamic extent of local-expand. The last solution works, but requires that the user explicitly passes the appropriate internal definition context.

The second and third solutions cannot be applied in our case, because type expanders can be expanded outside of the scope in which they were defined and used, as explained the Interactions between type expanders and scopes section.

The current version of the type expander does not support a reliable alternative to syntax-local-value which takes into account local binding forms for types (Let, ∀ and Rec), but one could be implemented, either by using some tricks to make the first solution work, or by providing an equivalent to syntax-local-value which consults the (tl-redirections) binding table.

E.1.5 Expanding types

The expand-type function fully expands the type stx. As explained in Locally binding type expanders, shadowing would be better handled using scopes. The expand-type function starts by defining some syntax classes, then parses stx, which can fall in many different cases.

«expand-type» ::=

(define (expand-type stx [applicable? #f])
  (start-tl-redirections
   «expand-type-syntax-classes»
   (define (expand-type-process stx first-pass?)
     «expand-type-debug-before»
     ((λ (result) «expand-type-debug-after»)
      (parameterize («expand-type-debug-indent»)
        «expand-type-debug-rules»
        (syntax-parse stx
          «expand-type-case-:»
          «expand-type-case-expander»
          «expand-type-case-∀-later»
          «expand-type-case-Λ-later»
          «expand-type-case-app-expander»
          «expand-type-case-∀-through»
          «expand-type-case-Rec»
          «expand-type-case-app-Λ»
          «expand-type-case-just-Λ/not-applicable»
          «expand-type-case-∀-app»
          «expand-type-case-Let»
          «expand-type-case-Letrec»
          «expand-type-case-noexpand»

          ;Must be after other special application cases
          «expand-type-case-app-other»
          «expand-type-case-app-fallback»
          «expand-type-case-fallback-T»))))
   (expand-type-process stx #t)))

E.1.5.1 Cases handled by expand-type

The cases described below which expand a use of a type expander re-expand the result, by calling expand-type once more. This process is repeated until no more expansion can be performed. This allows type expanders to produce calls to other type expanders, exactly like macros can produce calls to other macros.

We distinguish the expansion of types which will appear as the first element of their parent form from types which will appear in other places. When the applicable? argument to expand-type is #true, it indicates that the current type, once expanded, will occur as the first element of its enclosing form. If the expanded type is the name of a type expander, or a ∀ or Λ form, it will be directly applied to the given arguments by the type expander. When applicable? is #false, it indicates that the current type, once expanded, will not appear as the first element of its enclosing form (it will appear in another position, or it is at the top of the syntax tree representing the type).

When applicable? is #true, if the type is the name of a type expander, or a ∀ or Λ form, it is not expanded immediately. Instead, the outer form will expand it with the arguments. Otherwise, these forms are expanded without arguments, like identifier macros would be.

E.1.5.2 Applying type expanders

When a type expander is found in a non-applicable position, it is called, passing the identifier itself to the expander. An identifier macro would be called in the same way.

«expand-type-case-expander»1 ::=

[expander:type-expander
#:when (not applicable?)
(rule id-expander/not-applicable
   (let ([ctxx (make-syntax-introducer)])
     (expand-type (ctxx (apply-type-expander #'expander.code
                                             (ctxx #'expander)))
                  applicable?)))]

When a type expander is found in an applicable position, it is returned without modification, so that the containing application form may expand it with arguments. When the expander e appears as (e . args), it is applicable. It is also applicable when it appears as ((Let (bindings…) e) . args), for example, because Let propagates its applicable? status.

«expand-type-case-expander»2 ::=

[expander:type-expander
#:when applicable?
(rule id-expander/applicable
#'expander)]

When a form contains a type expander in its first element, the type expander is called. The result is re-expanded, so that a type expander can expand to a use of another type expander.

«expand-type-case-app-expander» ::=

[(~and expander-call-stx (expander:type-expander . _))
(rule app-expander
   (let ([ctxx (make-syntax-introducer)])
     (expand-type (ctxx (apply-type-expander #'expander.code
                                             (ctxx #'expander-call-stx)))
                  applicable?)))]

When a form of the shape (f . args) is encountered, and the f element is not a type expander, the f form is expanded, and the whole form (with f replaced by its expansion) is expanded a second time. The applicable? parameter is set to #true while expanding f, so that if f produces a type expander (e.g. f has the shape (Let (…) some-type-expander)), the type expander can be applied to the args arguments.

«expand-type-case-app-other» ::=

[(~and whole (f . args))
#:when first-pass?
(rule app-other
   (expand-type-process
    (datum->syntax #'whole
                   (cons (expand-type #'f #true) #'args)
                   #'whole
                   #'whole)
    #f))]

E.1.5.2.1 Polymorphic types with ∀

When the ∀ or All special forms from typed/racket are used, the bound type variables may shadow some type expanders. The type expanders used in the body T which have the same identifier as a bound variable will be affected by this (they will not act as a type-expander anymore). The body of the ∀ or All form is expanded with the modified environment. The result is wrapped again with (∀ (TVar …) expanded-T), in order to conserve the behaviour from typed/racket’s ∀.

«expand-type-case-∀-through» ::=

[({~and ∀ {~literal ∀}} (tvar:id …) T:type)
#:when (not applicable?)
(rule just-∀/not-applicable
   (with-syntax ([(tvar-vars-only …) (remove-ddd #'(tvar …))])
     (with-bindings [(tvar-vars-only …) (stx-map «shadowed»
                                                 #'(tvar-vars-only …))]
                    (T tvar …)
       #`(∀ (tvar …)
            #,(expand-type #'T #f)))))]

Where «shadowed» is used to bind the type variables tvarᵢ to (No-Expand tvarᵢ), so that their occurrences are left intact by the type expander:

«shadowed» ::=

(λ (_τ)
  (make-type-expander
   (λ (stx)
     (syntax-case stx ()
       [self (identifier? #'self) #'(No-Expand self)]
       [(self . args) #'((No-Expand self) . args)]))))

When a ∀ polymorphic type is found in an applicable position, it is returned without modification, so that the containing application form may expand it, binding the type parameters to their effective arguments.

«expand-type-case-∀-later» ::=

[(~and whole ({~literal ∀} (tvar:id …) T:type))
#:when applicable?
(rule just-∀/applicable
#'whole)]

When a ∀ polymorphic type is immediately applied to arguments, the type expander attempts to bind the type parameters to the effective arguments. It currently lacks any support for types under ellipses, and therefore that case is currently handled by the «expand-type-case-app-fallback» case described later.

«expand-type-case-∀-app» ::=

[(({~literal ∀} ({~and tvar:id {~not {~literal …}}} …) τ) arg …)
(unless (= (length (syntax->list #'(tvar …)))
            (length (syntax->list #'(arg …))))
   «app-args-error»)
(rule app-∀
   (with-bindings [(tvar …) (stx-map (λ (a) (make-type-expander (λ (_) a)))
                                         #'(arg …))]
                      τ
         (expand-type #'τ applicable?)))]

If the given number of arguments does not match the expected number of arguments, an error is raised immediately:

«app-args-error» ::=

(raise-syntax-error
'type-expander
(format (string-append "Wrong number of arguments to "
                        "polymorphic type: ~a\n"
                        "  expected: ~a\n"
                        "  given: ~a"
                        "  arguments were...:\n")
         (syntax->datum #'f)
         (length (syntax->list #'(tvar …)))
         (length (syntax->list #'(arg …)))
         (string-join
          (stx-map (λ (a)
                     (format "~a" (syntax->datum a)))
                   #'(arg …))
          "\n"))
#'whole
#'∀
(syntax->list #'(arg …)))

E.1.5.2.2 Recursive types with Rec

Similarly, the Rec special form will cause the bound variable R to shadow type expanders with the same name, within the extent of the body T. The result is wrapped again with (Rec R expanded-T), in order to conserve the behaviour from typed/racket’s Rec.

«expand-type-case-Rec» ::=

[((~literal Rec) R:id T:type)
(rule Rec
   #`(Rec R #,(with-bindings [R («shadowed» #'R)]
                                 T
                    (expand-type #'T #f))))]

E.1.5.2.3 Local bindings with Let and Letrec

The Let special form binds the given identifiers to the corresponding type expanders. We use with-bindings, as explained above in (part ("(lib type-expander/type-expander.hl.rkt)" "shadow")), to bind the Vᵢ … identifiers to their corresponding Eᵢ while expanding T.

«expand-type-case-Let» ::=

[((~commit (~literal Let)) ([Vᵢ:id Eᵢ] …) T:type)
(rule Let
   (with-bindings [(Vᵢ …)
                   (stx-map (λ (Eᵢ)
                              (make-type-expander
                               (λ (stx)
                                 (syntax-case stx ()
                                   [self (identifier? #'self) Eᵢ]
                                   [(self . argz) #`(#,Eᵢ . argz)]))))
                            #'(Eᵢ …))]
                  T
     (expand-type #'T applicable?)))]

The Letrec special form behaves in a similar way, but uses with-rec-bindings, so that the right-hand-side expressions Eᵢ appear to be within the scope of all the Vᵢ bindings.

«expand-type-case-Letrec» ::=

[((~commit (~literal Letrec)) ([Vᵢ:id Eᵢ] …) T:type)
(rule Letrec
   (with-rec-bindings [(Vᵢ …)
                       (λ (Eᵢ)
                         (make-type-expander
                          (λ (stx)
                            (syntax-case stx ()
                              [self (identifier? #'self) Eᵢ]
                              [(self . args444) #`(#,Eᵢ . args444)]))))
                       Eᵢ]
                      T
     (expand-type #'T applicable?)))]

E.1.5.2.4 Anonymous types with Λ

When an anonymous type expander appears as the first element of its enclosing form, it is applied to the given arguments. We use the trampoline-eval function defined in another file, which evaluates the given quoted transformer expression, while limiting the issues related to scopes. The “official” eval function from racket/base removes one of the module scopes which are normally present on the expression to evaluate. In our case, we are evaluating an anonymous type expander, i.e. a transformer function. When using eval, identifiers generated by the transformer function may not have the expected bindings. The alternative trampoline-eval seems to solve this problem.

The auto-syntax-case form is used, so that an anonymous type expander (Λ (_ a b) …) can either use a and b as pattern variables in quoted syntax objects, or as regular values (i.e syntax->datum is automatically applied on the syntax pattern variables when they are used outside of syntax templates, instead of throwing an error).

«eval-anonymous-expander-code» ::=

(trampoline-eval
#'(λ (stx)
     (define ctxx (make-syntax-introducer))
     (ctxx (auto-syntax-case (ctxx (stx-cdr stx)) ()
             [formals (let () . body)]))))

This case works by locally binding a fresh identifier tmp to a type expander, and then applying that type expander. It would also be possible to immediately invoke the type expander function.

«expand-type-case-app-Λ» ::=

[{~and whole (({~literal Λ} formals . body) . _args)}
;; TODO: use the same code as for the not-applicable case, to avoid ≠
(rule app-Λ
   (with-syntax* ([tmp (gensym '#%Λ-app-)]
                  [call-stx #'(tmp . whole)])
     (with-bindings [tmp (make-type-expander
                          «eval-anonymous-expander-code»)]
                    call-stx
       (expand-type #'call-stx applicable?))))]

When a Λ anonymous type expander appears on its own, in a non-applicable position, it is expanded like an identifier macro would be.

This case is implemented like the «expand-type-case-app-Λ» case, i.e. by locally binding a fresh identifier tmp to a type expander, and then applying that type expander. The difference is that in the identifier macro case, the syntax object given as an argument to the type expander contains only the generated tmp identifier. This allows the type expander to easily recognise the identifier macro case, where the whole syntax form is an identifier, from regular applications, where the whole syntax form is a syntax pair. The whole original syntax is attached consed onto a syntax property named 'original-Λ-syntax, in (unlikely) case the type expander needs to access the original Λ syntax used to call it (this is an experimental feature, and may change without notice in later versions).

«expand-type-case-just-Λ/not-applicable» ::=

[{~and whole ({~literal Λ} formals . body)}
#:when (not applicable?)
(rule just-Λ/not-applicable
   (with-syntax* ([tmp (syntax-property
                        (datum->syntax #'whole
                                       (gensym '#%Λ-id-macro-)
                                       #'whole
                                       #'whole)
                        'original-Λ-syntax
                        (cons #'whole
                              (or (syntax-property #'whole
                                                   'original-Λ-syntax)
                                  null)))]
                  [call-stx #'(tmp . tmp)])
         (with-bindings [tmp (make-type-expander
                              «eval-anonymous-expander-code»)]
                        call-stx
           ;; applicable? should be #f here, otherwise it would have been
           ;; caught by other cases.
           (expand-type #'call-stx applicable?))))]

When a Λ anonymous type expander appears on its own, in an applicable position, it is returned without modification, so that the containing application form may expand it with arguments (instead of expanding it like an identifier macro would be).

«expand-type-case-Λ-later» ::=

[(~and whole ({~literal Λ} formals . body))
#:when applicable?
(rule just-Λ/applicable
#'whole)]

E.1.5.2.5 Preventing the expansion of types with No-Expand

The No-Expand special form prevents the type expander from re-expanding the result. This is useful for example for the implementation of the fancy quote expander, which relies on the built-in quote expander. It is also used to implement shadowing: type variables bound by ∀ in non-applicable positions and type variables bound by Rec are re-bound to type expanders returning (No-Expand original-tvar).

«expand-type-case-noexpand» ::=

[((~literal No-Expand) T)
(rule just-No-Expand
#'T)]
[(((~literal No-Expand) T) arg ...)
(rule app-No-Expand
#`(T #,@(stx-map (λ (τ) (expand-type τ #f)) #'(arg ...))))]

E.1.5.2.6 The overloaded : identifier

This case handles the colon identifiers : (overloaded by this library) and : (provided by typed/racket). Wherever the new overloaded : identifier appears in a type, we want to convert it back to the original : from typed/racket. The goal is that a type of the form (→ Any Boolean : Integer), using the new :, will get translated to (→ Any Boolean : Integer), using the old : so that it gets properly interpreted by typed/racket’s parser.

«expand-type-case-:» ::=

[(~and c (~literal new-:))
(rule (datum->syntax #'here ': #'c #'c)
':)]

E.1.5.2.7 Last resort cases: leaving the type unchanged

If the type expression to expand was not matched by any of the above cases, then it can still be an application of a polymorphic type T. The arguments TArg … can contain uses of type expanders. We therefore expand each separately, and combine the results.

«expand-type-case-app-fallback» ::=

[{~and whole (T TArg …)}
(rule app-fallback
(quasisyntax/loc #'whole
(T #,@(stx-map (λ (a) (expand-type a #f)) #'(TArg ...)))))]

As a last resort, we consider that the type T (which would most likely be an identifier) is either a built-in type provided by typed/racket, or a user-declared type introduced by define-type. In both cases, we just leave the type as-is.

«expand-type-case-fallback-T» ::=

[T
(rule just-fallback
#'T)]

E.1.5.3 Debugging type expanders

In order to facilitate writing type expanders, it is possible to print the inputs, steps and outputs of the expander using (debug-type-expander #t), which sets the value of debug-type-expander?. This can then be undone using (debug-type-expander #f).

«expand-type-debug-outer»1 ::=

(define debug-type-expander? (box #f))

«debug-type-expander» ::=

(define-syntax (debug-type-expander stx)
  (syntax-case stx ()
    [(_ #t) (set-box! debug-type-expander? #t) #'(void)]
    [(_ #f) (set-box! debug-type-expander? #f) #'(void)]))

For better readability, each level of recursion indents the debugging information:

«expand-type-debug-outer»2 ::=

(define indent (make-parameter 0))

«expand-type-debug-indent» ::=

[indent (+ (indent) 3)]

Before expanding a term, it is printed:

«expand-type-debug-before» ::=

(when (unbox debug-type-expander?)
  (printf "~a~a ~a"
          (make-string (indent) #\space)
          applicable?
          (+scopes stx)))

Once the term has been expanded, the original term and the expanded term are printed:

«expand-type-debug-after» ::=

(when (unbox debug-type-expander?)
  (printf "~a~a ~a\n~a=> ~a (case: ~a)\n"
          (make-string (indent) #\space)
          applicable?
          (+scopes stx)
          (make-string (indent) #\space)
          (+scopes (car result))
          (cdr result))
  (when (= (indent) 0)
    (print-full-scopes)))
(car result)

Finally, each rule for the type expander is wrapped with the rule macro, which prints the name of the rule, and returns a pair containing the result and the rule’s name, so that the debugging information indicates the rule applied at each step.

«expand-type-debug-rules» ::=

(define-syntax-rule (rule name e)
  (begin (when (unbox debug-type-expander?)
           (printf "(case:~a)\n"
                   'name))
         (cons e 'name)))

E.1.6 Overloading typed/racket forms

Throughout this section, we provide alternative definitions of the typed/racket forms :, lambda, define, struct, ann, inst… . We write these definitions with syntax-parse, using the syntax classes defined in section syntax classes.

Most of the time, we will use the experimental template macro from syntax/parse/experimental/template which allows more concise code than the usual #'() and #`().

E.1.6.1 syntax classes

The syntax classes from typed-racket/base-env/annotate-classes match against the : literal. Since we provide a new definition for it, these syntax classes do not match code using our definition of :. We therefore cannot use the original implementations of curried-formals and lambda-formals, and instead have to roll out our own versions.

We take that as an opportunity to expand the types directly from the syntax classes using #:with, instead of doing that inside the macros that use them.

The colon syntax class records the identifier it matches as a "disappeared use", which means that DrRacket will draw an arrow from the library importing it (either typed/racket or type-expander) to the identifier. Unfortunately, this effect is not (yet) undone by syntax/parse’s backtracking. See https://groups.google.com/forum/#!topic/racket-users/Nc1klmsj9ag for more details about this.

«remove-ddd» ::=

(define (remove-ddd stx)
(remove #'(... ...) (syntax->list stx) free-identifier=?))

«syntax-classes»1 ::=

(define-syntax-class colon
  #:attributes ()
  (pattern (~and {~or {~literal new-:} {~literal :}}
                 C
                 {~do (record-disappeared-uses (list #'C))})))

(define-splicing-syntax-class new-maybe-kw-type-vars
  #:attributes ([vars 1] maybe)
  (pattern kw+vars:lambda-type-vars
           #:with (vars …) (remove-ddd #'kw+vars.type-vars)
           #:with maybe #'kw+vars)
  (pattern (~seq)
           #:with (vars …) #'()
           #:attr maybe #f))

(define-splicing-syntax-class new-maybe-type-vars
  #:attributes ([vars 1] maybe)
  (pattern v:type-variables
           #:with (vars …) (remove-ddd #'v)
           #:with maybe #'v)
  (pattern (~seq)
           #:with (vars …) #'()
           #:attr maybe #f))

(define-splicing-syntax-class new-kw-formal
  #:attributes ([expanded 1])
  (pattern (~seq kw:keyword id:id)
           #:with (expanded ...) #'(kw id))
  (pattern (~seq kw:keyword [id:id
                             (~optional (~seq :colon type:type-expand!))
                             (~optional default:expr)])
           #:with (expanded ...)
           (template (kw [id (?@ : type.expanded)
                          (?? default)]))))

(define-splicing-syntax-class new-mand-formal
  #:attributes ([expanded 1])
  (pattern id:id
           #:with (expanded ...) #'(id))
  (pattern [id:id :colon type:type-expand!]
           #:with (expanded ...)
           (template ([id : type.expanded])))
  (pattern kw:new-kw-formal
           #:with (expanded ...) #'(kw.expanded ...)))

(define-splicing-syntax-class new-opt-formal
  #:attributes ([expanded 1])
  (pattern [id:id
            (~optional (~seq :colon type:type-expand!))
            default:expr]
           #:with (expanded ...)
           (template ([id (?? (?@ : type.expanded))
                       default])))
  (pattern kw:new-kw-formal
           #:with (expanded ...) #'(kw.expanded ...)))

(define-syntax-class new-rest-arg
  #:attributes ([expanded 0])
  (pattern rest:id
           #:with expanded #'rest)
  (pattern (rest:id
            :colon type:type-expand!
            (~or (~and x* (~describe "*" (~or (~literal *)
                                              (~literal ...*))))
                 (~seq (~literal ...) bound:type-expand!)))
           #:with expanded
           (template (rest : type.expanded
                           (?? x*
                               (?@ (... ...) bound.expanded))))))

(define-syntax-class new-lambda-formals
  (pattern (~or (mand:new-mand-formal ...
                 opt:new-opt-formal ...
                 . rest:new-rest-arg)
                (mand:new-mand-formal ...
                 opt:new-opt-formal ...))
           ;; TODO: once template supports ?? in tail position, use it.
           #:with expanded #`(mand.expanded ...
                              ...
                              opt.expanded ...
                              ...
                              . #,(if (attribute rest)
                                      #'rest.expanded
                                      #'()))))

(define-syntax-class (new-curried-formals def-id)
  (pattern (f:id . args:new-lambda-formals)
           #:with expanded #`(#,def-id . args.expanded))
  (pattern ((~var lhs (new-curried-formals def-id))
            . args:new-lambda-formals)
           #:with expanded #'(lhs.expanded . args.expanded)))

(define-syntax-class new-curried-formals-id
  (pattern (id:id . _))
  (pattern (lhs:new-curried-formals-id . _)
           #:with id #'lhs.id))

(define-splicing-syntax-class new-optionally-annotated-name
  (pattern (~seq name:id (~optional (~seq :colon type:type-expand!)))
           #:with expanded
           (template (name
                      (?? (?@ : type.expanded))))))

(define-syntax-class new-name-or-parenthesised-annotated-name
  (pattern name:id
           #:with expanded #'name)
  (pattern [id:id :colon type:type-expand!]
           #:with expanded
           (template [id : type.expanded])))

E.1.6.2 Overview of the overloaded primitives

The following sections merely define overloads for the typed/racket primitives. The process is similar each time: a new primitive is defined, e.g. new-: for :. The new primitive calls the old one, after having expanded (using expand-type) all parts of the syntax which contain types. Aside from heavy usage of syntax-parse, there is not much to say concerning these definitions.

E.1.6.3 :

«:» ::=

(set-:-impl! (syntax-parser
[(_ x:id t:expr)
#`(: x #,(expand-type #'t #f))]))

E.1.6.4 define-type

«define-type» ::=

(define-syntax new-define-type
  (syntax-parser
    [(_ (~or name:id (name:id maybe-tvar:id …)) . whole-rest)
     #:with (tvar …) (if (attribute maybe-tvar) #'(maybe-tvar …) #'())
     #:with (tvar-not-ooo …) (filter (λ (tv) (not (free-identifier=? tv #'(… …))))
                                     (syntax->list #'(tvar …)))
     (start-tl-redirections
      (with-bindings [(tvar-not-ooo …) (stx-map «shadowed»
                                                #'(tvar-not-ooo …))]
                     whole-rest
        (syntax-parse #'whole-rest
          [(type:type-expand! . rest)
           (template
            (define-type (?? (name tvar …) name)
              type.expanded
              . rest))])))]))

E.1.6.5 define

«define» ::=

(define-syntax new-define
  (f-start-tl-redirections
   (syntax-parser
     [(_ {~and (~seq :new-maybe-kw-type-vars
                     (~or v:id
                          formals-id:new-curried-formals-id)
                     _ …)
              (~with-tvars (tvars new-maybe-kw-type-vars)
                           (~or :id
                                (~var formals (new-curried-formals
                                               #'formals-id.id)))
                           (~optional (~seq :colon type:type-expand!))
                           e ...)})
      (template
       (define (?? (?@ . tvars.maybe)) (?? v formals.expanded)
         (?? (?@ : type.expanded))
         e ...))])))

E.1.6.6 lambda

«lambda» ::=

(define-syntax new-lambda
  (f-start-tl-redirections
   (syntax-parser
     [(_ {~with-tvars (tvars new-maybe-kw-type-vars)
              args:new-lambda-formals
              (~optional (~seq :colon ret-type:type-expand!))
              e …})
      (template (lambda (?? (?@ . tvars.maybe)) args.expanded
                  (?? (?@ : ret-type.expanded))
                  e ...))])))

E.1.6.7 case-lambda

«case-lambda» ::=

(define-syntax new-case-lambda
  (f-start-tl-redirections
   (syntax-parser
     [(_ {~with-tvars (tvars new-maybe-kw-type-vars)
              [args:new-lambda-formals
               (~optional (~seq :colon ret-type:type-expand!))
               e …]
              …})
      (template (case-lambda
                  (?? (?@ #:∀ tvars.maybe))
                  [args.expanded
                   (?? (ann (let () e …) ret-type.expanded)
                       (?@ e …))]
                  …))])))

E.1.6.8 struct

The name must be captured outside of the ~with-tvars, as ~with-tvars introduces everything in a new lexical context.

«struct» ::=

(define-syntax new-struct
  (f-start-tl-redirections
   (syntax-parser
     [(_ (~and
          (~seq :new-maybe-type-vars
                (~and (~seq name+parent …)
                      (~or (~seq name:id)
                           (~seq name:id parent:id)))
                _ …)
          {~with-tvars (tvars new-maybe-type-vars)
              (~or (~seq :id)
                   (~seq :id :id))
              ([field:id :colon type:type-expand!] ...)
              rest …}))
      (template (struct (?? tvars.maybe) name (?? parent)
                  ([field : type.expanded] ...)
                  rest …))])))

E.1.6.9 define-struct/exec

«define-struct/exec» ::=

(define-syntax (new-define-struct/exec stx)
  (syntax-parse stx
    [(_ (~and name+parent (~or name:id [name:id parent:id]))
        ([field:id (~optional (~seq :colon type:type-expand!))] ...)
        [proc :colon proc-type:type-expand!])
     (template (define-struct/exec name+parent
                 ([field (?? (?@ : type.expanded))] ...)
                 [proc : proc-type.expanded]))]))

E.1.6.10 ann

«ann» ::=

(define-syntax/parse (new-ann value:expr
(~optional :colon) type:type-expand!)
(template (ann value type.expanded)))

E.1.6.11 cast

«cast» ::=

(define-syntax/parse (new-cast value:expr type:type-expand!)
(template (cast value type.expanded)))

E.1.6.12 unsafe-cast

We additionally define an unsafe-cast macro, which Typed/Racket does not provide yet, but can easily be defined using unsafe-require/typed and a polymorphic function.

«unsafe-cast» ::=

(module m-unsafe-cast typed/racket
  (provide unsafe-cast-function)
  (define (unsafe-cast-function [v : Any]) v))

(require (only-in typed/racket/unsafe unsafe-require/typed))
(unsafe-require/typed 'm-unsafe-cast
                      [unsafe-cast-function (∀ (A) (→ Any A))])

(define-syntax-rule (unsafe-cast/no-expand v t)
  ((inst unsafe-cast-function t) v))

(define-syntax/parse (unsafe-cast value:expr type:type-expand!)
  (template (unsafe-cast/no-expand value type.expanded)))

E.1.6.13 inst

«inst» ::=

(define-syntax new-inst
  (syntax-parser
    [(_ v (~optional :colon) t:type-expand! ...
        last:type-expand! (~literal ...) b:id)
     (template (inst v
                     t.expanded ...
                     last.expanded (... ...) b))]
    [(_ v (~optional :colon) t:type-expand! ...)
     (template (inst v t.expanded ...))]))

E.1.6.14 row-inst

«row-inst» ::=

(define-syntax/parse (new-inst e row:type-expand!)
(template (row-inst e row.expanded)))

E.1.6.15 let

«let» ::=

(define-syntax new-let
  (f-start-tl-redirections
   (syntax-parser
     [(_ (~optional (~seq loop:id
                          (~optional
                           (~seq :colon return-type:type-expand!))))
         (~with-tvars (tvars new-maybe-kw-type-vars)
                      ([name:new-optionally-annotated-name e:expr] ...)
                      rest ...))
      (template
       (let (?? (?@ loop (?? (?@ : return-type.expanded))))
         (?@ . tvars)
         ([(?@ . name.expanded) e] ...)
         rest ...))])))

E.1.6.16 let*

«let*» ::=

(define-syntax/parse
    (new-let*
     ([name:new-optionally-annotated-name e:expr] ...)
     . rest)
  (template
   (let* ([(?@ . name.expanded) e] ...) . rest)))

E.1.6.17 let-values

«let-values» ::=

(define-syntax/parse
    (new-let-values
     ([(name:new-name-or-parenthesised-annotated-name ...) e:expr] ...)
     . rest)
  (template
   (let-values ([(name.expanded ...) e] ...)
     . rest)))

E.1.6.18 make-predicate

«make-predicate» ::=

(define-simple-macro (new-make-predicate type:type-expand!)
(make-predicate type.expanded))

E.1.6.19 :type, :print-type, :query-type/args, :query-type/result

«:type» ::=

(define-syntax/parse (new-:type (~optional (~and verbose #:verbose))
                                type:type-expand!)
  (template (eval #'(#%top-interaction
                     . (:type (?? verbose) type.expanded)))))

«:print-type» ::=

(define-syntax/parse (new-:print-type e:expr)
  #'(:print-type e)
  #'(eval #'(#%top-interaction
             . (:print-type e))))

«:query-type/args» ::=

(define-syntax/parse (new-:query-type/args f type:type-expand! …)
#'(eval #'(#%top-interaction
. (:query-type/args f type.expanded …))))

«:query-type/result» ::=

(define-syntax/parse (new-:query-type/result f type:type-expand!)
#'(eval #'(#%top-interaction
. (:query-type/result f type.expanded))))

E.1.6.20 Type expanders for the typed classes

Not all forms are supported for now.

«syntax-classes»2 ::=

(define-syntax-class field-decl
  (pattern id:id #:with expanded #'(field id))
  (pattern (maybe-renamed {~optional {~seq :colon type:type-expand!}}
                          {~optional default-value-expr})
           #:with expanded
           (template (maybe-renamed (?? (?@ : type.expanded))
                                    (?? default-value-expr)))))

«syntax-classes»3 ::=

(define-syntax-class field-clause
  #:literals (field)
  (pattern (field field-decl:field-decl …)
           #:with expanded (template (field field-decl.expanded …))))

«syntax-classes»4 ::=

(define-syntax-class super-new-clause
  #:literals (super-new)
  (pattern (super-new . rest)
           #:with expanded (template (super-new . rest))))

«syntax-classes»5 ::=

(define-syntax-class class-clause
  #:attributes (expanded)
  (pattern :field-clause)
  (pattern :super-new-clause))

«class» ::=

(define-syntax new-class
  (f-start-tl-redirections
   (syntax-parser
     [(_ superclass-expr
         {~with-tvars (tvars new-maybe-kw-type-vars)
              clause:class-clause ...})
      (template (class superclass-expr
                  (?? (?@ . tvars.maybe))
                  clause.expanded ...))])))

E.1.6.21 Other typed/racket forms

The other typed/racket forms below do not have an alternative definition yet.

«other-forms» ::=

(define-syntax (missing-forms stx)
  (syntax-parse stx
    [(_ name ...)
     (define/with-syntax (tmp ...) (generate-temporaries #'(name ...)))
     #'(begin
         (begin
           (define-syntax (tmp stx)
             (raise-syntax-error
              'name
              (format "~a not implemented yet for type-expander" 'name)
              stx))
           (provide (rename-out [tmp name])))
         ...)]))

(missing-forms
;;TODO: add all-defined-out in prims.rkt
;; top-interaction.rkt
;:type
;:print-type
;:query-type/args
;:query-type/result
;; case-lambda.rkt
;case-lambda
;case-lambda:
pcase-lambda:
;; (submod "prims-contract.rkt" forms)
require/opaque-type
;require-typed-struct-legacy
require-typed-struct
;require/typed-legacy
require/typed
require/typed/provide
require-typed-struct/provide
;cast
;make-predicate
define-predicate
;; prims.rkt
define-type-alias
define-new-subtype
define-typed-struct
define-typed-struct/exec
;ann
;inst
;:
define-struct:
define-struct
;struct
struct:
λ:
lambda:
;lambda
;λ
;define
;let
;let*
letrec
;let-values
letrec-values
let/cc
let/ec
let:
let*:
letrec:
let-values:
letrec-values:
let/cc:
let/ec:
for
for/list
for/vector
for/hash
for/hasheq
for/hasheqv
for/and
for/or
for/sum
for/product
for/lists
for/first
for/last
for/fold
for*
for*/list
for*/lists
for*/vector
for*/hash
for*/hasheq
for*/hasheqv
for*/and
for*/or
for*/sum
for*/product
for*/first
for*/last
for*/fold
for/set
for*/set
do
do:
with-handlers
define-struct/exec:
;define-struct/exec)

E.1.7 Future work

We have not implemented alternative type-expanding definitions for all the typed/racket forms, as noted in Other typed/racket forms.

Integrating the type expander directly into typed/racket would avoid the need to provide such definitions, and allow using type expanders in vanilla typed/racket, instead of having to require this library. However, the code wrapping the typed/racket forms could be re-used by other libraries that alter the way typed/racket works, so implementing the remaining forms could still be useful.

Also, we would need to provide a syntax-local-type-introduce function, similar to the syntax-local-match-introduce function provided by match for example.

E.1.8 Conclusion

When an identifier is required from another module, it is not the same as the one visible within the defining module. This is a problem for :, because we match against it in our syntax classes, using (~literal :), but when it is written in another module, for example (define foo : Number 42), it is not the same identifier as the one used by original definition of :, and therefore the (~literal :) won’t match. I suspect that issue to be due to contract wrappers added by typed/racket.

To get around that problem, we define : in a separate module, and require it in the module containing the syntax classes:

Since our new-: macro needs to call the type-expander, and the other forms too, we cannot define type-expander in the same module as these forms, it needs to be either in the same module as new-:, or in a separate module. Additionally, expand-type needs to be required for-syntax by the forms, but needs to be provided too, so it is much easier if it is defined in a separate module (that will be used only by macros, so it will be written in racket, not typed/racket).

«module-expander» ::=

(module expander racket
  (require (for-template typed/racket
                         "identifiers.rkt")
           racket
           (only-in racket/base [... …])
           syntax/parse
           racket/format
           racket/syntax
           syntax/id-table
           syntax/stx
           auto-syntax-e
           "parameterize-lexical-context.rkt"
           debug-scopes
           racket/contract/base)
  ;; TODO: move this in a separate chunk and explain it

  (provide prop:type-expander
           (contract-out
            (rename has-prop:type-expander?
                    prop:type-expander?
                    (-> any/c boolean?))
            (rename get-prop:type-expander-value
                    prop:type-expander-ref
                    (-> has-prop:type-expander?
                        any/c)))
           type-expander
           apply-type-expander
           ;bind-type-vars
           expand-type
           type
           stx-type/c
           type-expand!
           debug-type-expander?
           patched
           make-type-expander)

  «remove-ddd»

  «prop-guard»
  «prop:type-expander»
  «type-expander-struct»

  «patched»

  «apply-type-expander»
  ;<expand-quasiquote>
  «type-syntax-class»
  «type-contract»
  «expand-type-debug-outer»
  «expand-type»
  «type-expand-syntax-class»)

We can finally define the overloaded forms, as well as the <define-type-expander> form.

«module-main» ::=

(module main typed/racket
  (require (only-in typed/racket/base [... …])
           typed/racket/class
           (for-syntax racket
                       (only-in racket/base [... …])
                       racket/syntax
                       syntax/parse
                       syntax/parse/experimental/template
                       syntax/id-table
                       "parameterize-lexical-context.rkt"
                       syntax/stx)
           (for-meta 2 racket/base syntax/parse)
           "utils.rkt"
           syntax/parse/define
           "identifiers.rkt")

  (require (submod ".." expander))
  (require (for-syntax (submod ".." expander)))
  (require (for-syntax typed-racket/base-env/annotate-classes))

  (provide prop:type-expander
           prop:type-expander?
           prop:type-expander-ref
           expand-type
           define-type-expander
           patch-type-expander
           Let
           Letrec
           Λ
           ...*
           No-Expand
           unsafe-cast/no-expand
           unsafe-cast
           debug-type-expander
           (rename-out [new-: :]
                       [new-define-type        define-type]
                       [new-define             define]
                       [new-lambda             lambda]
                       [new-lambda             λ]
                       [new-case-lambda        case-lambda]
                       [new-case-lambda        case-lambda:]
                       [new-struct             struct]
                       [new-define-struct/exec define-struct/exec]
                       [new-ann                ann]
                       [new-cast               cast]
                       [new-inst               inst]
                       [new-let                let]
                       [new-let*               let*]
                       [new-let-values         let-values]
                       [new-make-predicate     make-predicate]
                       [new-:type              :type]
                       [new-:print-type        :print-type]
                       [new-:query-type/args   :query-type/args]
                       [new-:query-type/result :query-type/result]
                       ;[new-field              field]
                       ;[new-super-new          super-new]
                       [new-class              class]))

  (begin-for-syntax
    (define-syntax ~with-tvars
      (pattern-expander
       (syntax-parser
         [(_ (tv tv-stxclass) pat ...)
          #'{~seq {~var tmp-tv tv-stxclass}
                  {~seq whole-rest (... ...)}
                  {~parse (({~var tv tv-stxclass}) pat ...)
                   ;; rebind tvars:
                   (with-bindings [(tmp-tv.vars (... ...))
                                   (stx-map «shadowed»
                                            #'(tmp-tv.vars (... ...)))]
                                  ;; rebind occurrences of the tvars within:
                                  (tmp-tv whole-rest (... ...))
                     ;; to (re-)parse:
                     #'(tmp-tv whole-rest (... ...)))}}]))))

  «debug-type-expander»

  «:»

  «define-type-expander»
  «patch»

  (begin-for-syntax
    «remove-ddd»
    «syntax-classes»

    (provide colon))

  «define-type»
  «define»
  «lambda»
  «case-lambda»
  «struct»
  «define-struct/exec»
  «ann»
  «cast»
  «unsafe-cast»
  «inst»
  «let»
  «let*»
  «let-values»
  «make-predicate»
  «:type»
  «:print-type»
  «:query-type/args»
  «:query-type/result»
  ;<field>
  «class»
  ;<super-new>
  «other-forms»)

We can now assemble the modules in this order:

«*» ::=

«module-expander»
«module-main»

(require 'main)
(provide (except-out (all-from-out 'main) (for-syntax colon)))

E.2 Some example type expanders

E.2.1 Example type expanders: quasiquote and quasisyntax

We define type expanders for quote, quasiquote, syntax and quasisyntax:

The next four special forms are implemented as type expanders with patch-type-expander because redefining their name (quote, quasiquote, syntax and quasisyntax) would conflict with existing identifiers. patch-type-expander uses a global persistant (across modules) for-syntax mutable table, which associates identifiers to type-expanders. typed/racket works in that way by associating data (their type) to existing identifiers. The mutable-match-lambda library on the other hand allows adding behaviour to an identifier after it is defined, but relies on some level of cooperation from that identifier, which may be less practical for built-in identifiers like quote. Relying on an external data structure to associate information with identifiers makes it possible to overload the meaning of quote or curry when used as a type expander, without having to alter their original definition. Another option would be to provide overloaded versions of these identifiers, to shadow those imported by the #lang module. This would however cause conflicts for curry when racket/function is explicitly required (instead of being required implicitly by #<procedure:hash-lang> racket, for example.

«quotes»1 ::=

(patch-type-expander quote
  (λ (stx)
    (syntax-case stx ()
      [(_ T)
       (expand-quasiquote 'quote 1 #'T)])))

«quotes»2 ::=

(patch-type-expander quasiquote
  (λ (stx)
    (syntax-case stx ()
      [(_ T)
       (expand-quasiquote 'quasiquote 1 #'T)])))

«quotes»3 ::=

(patch-type-expander syntax
  (λ (stx)
    (syntax-case stx ()
      [(_ T)
       (expand-quasiquote 'syntax 1 #'T)])))

«quotes»4 ::=

(patch-type-expander quasisyntax
  (λ (stx)
    (syntax-case stx ()
      [(_ T)
       (expand-quasiquote 'quasisyntax 1 #'T)])))

Their implementation is factored out into the expand-quasiquote for-syntax function. It is a reasonably complex showcase of this library’s functionality. typed/racket allows the use of quote to describe a type which contains a single inhabitant, the quoted datum. For example, (define-type foo '(a b (1 2 3) c)) declares a type foo which is equivalent to (List 'a 'b (List 1 2 3) 'c).

We build upon that idea to allow the use of syntax, quasiquote and quasisyntax. Both syntax and quasisyntax wrap each s-expression within the quoted datum with Syntaxof, which avoids the otherwise tedious declaration of the type for a piece of syntax. Both quasiquote and quasisyntax allow escaping the quoted datum (using unquote and unsyntax, respectively). A later version of this library could support unquote-splicing and unsyntax-splicing.

Using this type-expander, one can write

(define-type bar `(a ,Symbol (1 ,(U Number String) 3) c))

The above declaration gets expanded to:

(define-type bar (List 'a Symbol (List 1 (U Number String) 3) 'c))

The implementation of expand-quasiquote recursively traverses the type expression. The mode argument can be one of 'quote, 'quasiquote, 'syntax or 'quasisyntax. It is used to determine whether to wrap parts of the type with Syntaxof or not, and to know which identifier escapes the quoting (unquote or unsyntax). The depth argument keeps track of the quoting depth: in Racket `(foo `(bar ,baz)) is equivalent to (list 'foo (list 'quasiquote (list 'bar (list 'unquote 'baz)))) (two levels of unquote are required to escape the two levels of quasiquote), so we want the type to be (List 'foo (List 'quasiquote (List 'bar (List 'unquote 'baz)))).

«expand-quasiquote» ::=

(define (list*->list l)
  (if (pair? l)
      (cons (car l) (list*->list (cdr l)))
      (list l)))
(define (expand-quasiquote mode depth stx)
  (define (wrap t)
    (if (or (eq? mode 'syntax) (eq? mode 'quasisyntax))
        #`(Syntaxof #,t)
        t))
  (define (wrap-quote t)
    (if (or (eq? mode 'syntax) (eq? mode 'quasisyntax))
        #`(Syntaxof (No-Expand '#,t))
        #`(No-Expand '#,t)))
  (define expand-quasiquote-rec (curry expand-quasiquote mode depth))
  (syntax-parse stx
    [((~literal quote) T)
     (wrap #`(List #,(wrap-quote #'quote)
                   #,(expand-quasiquote-rec #'T)))]
    [((~literal quasiquote) T)
     (wrap #`(List #,(wrap-quote #'quasiquote)
                   #,(if (eq? mode 'quasiquote)
                         (expand-quasiquote mode (+ depth 1) #'T)
                         (expand-quasiquote-rec #'T))))]
    [((~literal unquote) T)
     (if (eq? mode 'quasiquote)
         (if (= depth 1)
             (expand-type #'T) ;; TODO: applicable? !!!!!!!!!!!!!!!!!!!!!!!!!!!!
             (wrap #`(List #,(wrap-quote #'unquote)
                           #,(expand-quasiquote mode (- depth 1) #'T))))
         (wrap #`(List #,(wrap-quote #'unquote)
                       #,(expand-quasiquote-rec #'T))))]
    [((~literal syntax) T)
     (wrap #`(List #,(wrap-quote #'quote)
                   #,(expand-quasiquote-rec #'T)))]
    [((~literal quasisyntax) T)
     (wrap #`(List #,(wrap-quote #'quasisyntax)
                   #,(if (eq? mode 'quasisyntax)
                         (expand-quasiquote mode (+ depth 1) #'T)
                         (expand-quasiquote-rec #'T))))]
    [((~literal unsyntax) T)
     (if (eq? mode 'quasisyntax)
         (if (= depth 1)
             (expand-type #'T) ;; TODO: applicable? !!!!!!!!!!!!!!!!!!!!!!!!!!!!
             (wrap #`(List #,(wrap-quote #'unsyntax)
                           #,(expand-quasiquote mode (- depth 1) #'T))))
         (wrap #`(List #,(wrap-quote #'unsyntax)
                       #,(expand-quasiquote-rec #'T))))]
    ;; TODO For lists, we should consider the cases where syntax-e gives
    ;; a pair vs the cases where it gives a list.
    [(T . U)
     #:when (syntax? (cdr (syntax-e stx)))
     (wrap #`(Pairof #,(expand-quasiquote-rec #'T)
                     #,(expand-quasiquote-rec #'U)))]
    [() (wrap #'Null)]
    [(T ...)
     #:when (list? (syntax-e stx))
     (wrap #`(List #,@(stx-map expand-quasiquote-rec #'(T ...))))]
    [whole
     #:when (pair? (syntax-e #'whole))
     #:with (T ... S) (list*->list (syntax-e #'whole))
     (wrap #`(List* #,@(stx-map expand-quasiquote-rec #'(T ... S))))]
    [#(T ...)
     (wrap #`(Vector #,@(stx-map expand-quasiquote-rec #'(T ...))))]
    [#&T (wrap #`(Boxof #,(expand-quasiquote-rec #'T)))]
    ; TODO: Prefab with #s(prefab-struct-key type ...)
    [T:id (wrap #'(No-Expand 'T))]
    [T #:when (string? (syntax-e #'T)) (wrap #'T)]
    [T:number (wrap #'T)]
    [T:keyword (wrap #'(No-Expand 'T))]
    [T:char (wrap #'T)]
    [#t (wrap #'True)]
    [#t (wrap #'False)]
    [_ (raise-syntax-error 'expand-quasiquoste
                           (format "Unknown quasiquote contents: ~a" stx)
                           stx)]))

E.2.2 Implementation of the Let* special type expander form

The Let* special form is implemented in terms of Let, binding each variable in turn:

«Let*» ::=

(define-type-expander (Let* stx)
  (syntax-case stx ()
    [(me ([var val] . rest) τ)
     (with-syntax ([L (datum->syntax #'here 'Let #'me #'me)]
                   [L* (datum->syntax #'here 'Let* #'me #'me)])
       #'(L ([var val])
            (L* rest
                τ)))]
    [(_ () τ) #'τ]))

E.2.3 curry

The curry special form takes a type expander (or a polymorphic type) and some arguments. The whole form should appear in the first position of its containing form, which contains more arguments, or be bound with a Let or Letrec. curry appends the arguments in the outer form to the whole inner form, and expands the result. This really should be implemented as a type expander so that the partially-applied expander or polymorphic type can be bound using Let, for example, but for now it is hardcoded here.

«curry» ::=

(patch-type-expander curry
  (λ (stx)
    (syntax-case stx ()
      [(_ T Arg1 ...)
       #'(Λ (_ . Args2) #'(T Arg1 ... . Args2))])))

E.2.4 Putting it all together

«*» ::=

(require "type-expander.hl.rkt"
         "identifiers.rkt"
         racket/function
         (for-syntax racket/base
                     (only-in racket/base [... …])
                     (submod "type-expander.hl.rkt" expander)
                     syntax/parse
                     syntax/stx
                     racket/function
                     racket/match))
(provide Let*)

«Let*»

(begin-for-syntax «expand-quasiquote»)
«quotes»

«curry»

1	Introduction
2	State of the art
3	Goals, constraints and examples
4	Typed Racket
5	Extensible type system and algebraic datatypes
6	Typed nanopass
7	Examples and results
8	Conclusion and future work directions
9	Bibliography
A	Ph.C Graph library: Implementation
B	Algebraic Data Types for compilers: Implementation
C	Implementation of Remember
D	Implementation of the multi-id library
E	Type expander: Implementation